系统模型与失真测度分析

本章论述问题仅涉及信源编码，因此在图5.l所示的通信系统中，可以将信道编码和信道译码看成是信道的一部分，组成一个广义信道。根据有噪信道编码定理（见第6章），可以把广义信道等价成一个无扰信道。这样收信者收到消息后所产生的失真（或误差）仅由信源编码产生。显然，若允许失真越大，信息传输率就越小；若允许失真越小，信息传输率就越大。所以，信息传输率与信源编码所引起的失真（或误差）是有关的。

为了定量地描述信息传输率和失真的关系，一方面可以略去广义无扰信道（因为该信道上信息传输没有失真）；另一方面可以把信源编码和信源译码等价成一个虚拟信道，由于是有失真编码，所以此虚拟信道不是一一对应的，可以用信道转移概率来描述编码前和译码后的关系，这就使图5.1的通信系统简化成图5.2所示的系统。一般将图5.2中的信道称为试验信道。

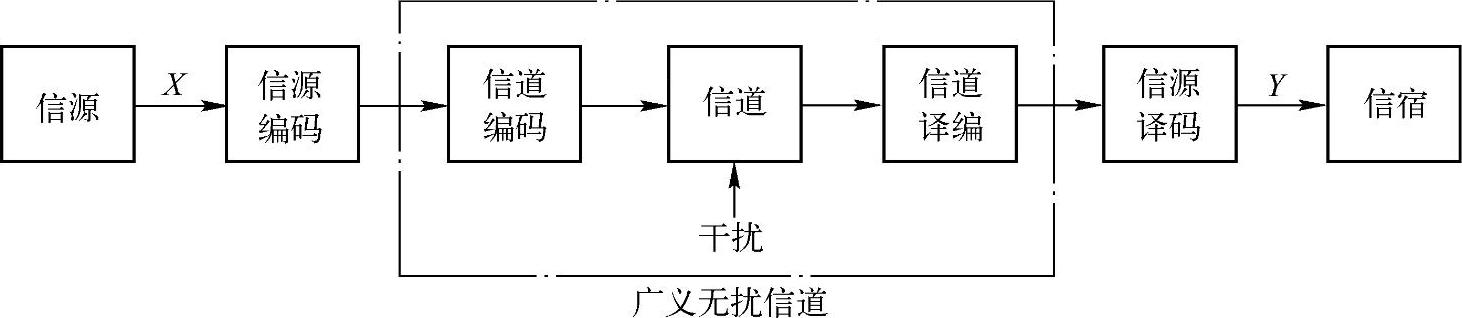
图5.1 通信系统

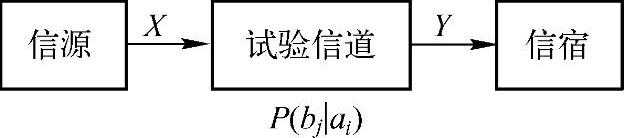
图5.2 简化的通信系统

对于离散信源，设试验信道的输入随机变量为X，值域为A：{a₁，a₂，…，a_r}；输出随机变量为Y，值域为B：{b₁，b₂，…，b_s}。X的概率分布为P（x）或P（a_i）（i=1，2，…，r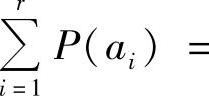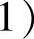；，Y的概率分布为P（y）或P（b_j）（j=1，2，…，。

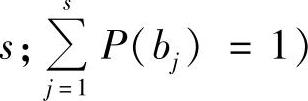为衡量信源编码所引起的失真，给出失真测度的定义如下：

定义5.1对于每一对（a_i，b_j），指定一个非负的函数d（a_i，b_j）≥0（i=1，2，…，r；j=1，2，…，s），称d（a_i，b_j）为单个符号的失真度或失真函数。

失真度d（a_i，b_j）表示信源发出符号a_i，在收信端再现为b_j所引起的误差或失真。通常，d（a_i，b_j）值的大小代表失真的大小；d（a_i，b_j）=0表示没有失真。

为了方便，将r×s个非负的d（a_i，b_j）排列成矩阵形式，即

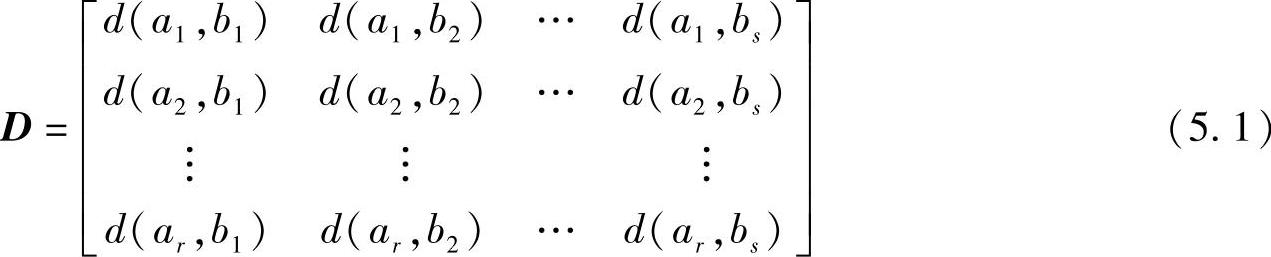
并称D为失真矩阵，它是一个r×s阶矩阵。

失真函数是根据人们的实际需要和失真引起的损失、风险大小等因素人为规定的。常用的失真函数有汉明失真（Hamming失真）、平方误差失真和删除失真。

定义5.2 在离散对称信道（r=s）中，Hamming失真定义为

由定义5.2知，Hamming失真矩阵D为r阶方阵，即

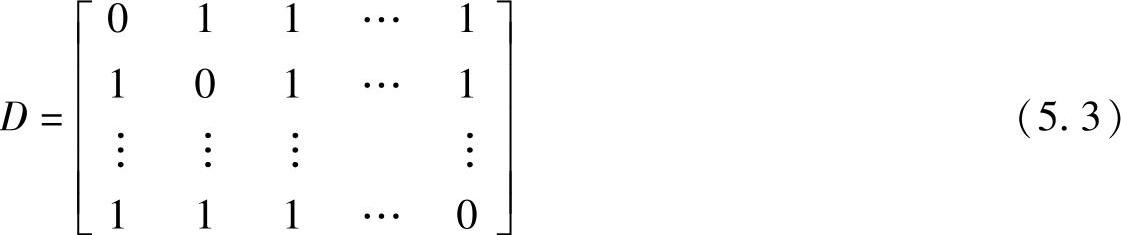
Hamming失真认为，当再现的接收符号与发送的信源符号相同时不存在失真和错误，所以失真度d（a_i，b_j）=0；当再现的接收符号与发送符号不同时存在失真，而且认为发送符号与再现符号不同时的失真都相同，所以失真度d（a_i，b_j）（a_i≠b_j）为非负常数，常取值为1。

【例5.1】

对于二元对称信道（r=s=2），信源X的符号集为A：{0，1}，接收变量Y的符号集为B：{0，1}。在Hamming失真定义下，可得失真矩阵为

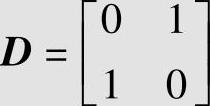
即d（0，0）=d（1，1）=0，d（0，1）=d（1，0）=1。

定义5.3 对于每一对（a_i，b_j），指定一个非负的函数

d（a_i，b_j）=（a_i-b_j）2，i=1，2，…，r且j=1，2，…，s（5.4）称d（a_i，b_j）为单个符号的平方误差失真度或平方误差失真函数。

平方误差失真认为，如果信道的输入和输出符号是信号的幅度值，则较大的幅度差值要比较小的幅度差值引起的失真更为严重，严重程度用平方表示。

【例5.2】

对于三元对称信道，信源X的符号集为A：{0，1，2}，接收变量Y的符号集为B：{0，1，2}。在平方误差失真定义下，可得失真矩阵为

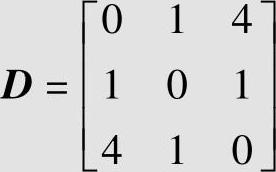
定义5.4 在删除信道（s=r+1）中，设接收符号b_s是删除符号，则删除失真定义为

删除失真认为，把信源符号再现为删除符号时，其失真程度要比再现为其他接收符号的失真程度少一半。

【例5.3】

对于二元删除信道（r=2，s=3），信源X的符号集为A：{0，1}，接收变量Y的符号集为B：{0，1，？}。在删除失真意义下，可得失真矩阵为

(www.xing528.com)

即d（0，0）=d（1，1）=0，d（0，1）=d（1，0）=1，d（0，？）=d（1，？）=1/2。

由于信源X和信宿Y都是随机变量，故单个符号失真度d（a_i，b_j）也是随机变量。为了衡量失真度对信息传输的总体影响，需要引入平均失真度的概念。

定义5.5 平均失真度定义为单个符号失真度d（a_i，b_j）的数学期望，即

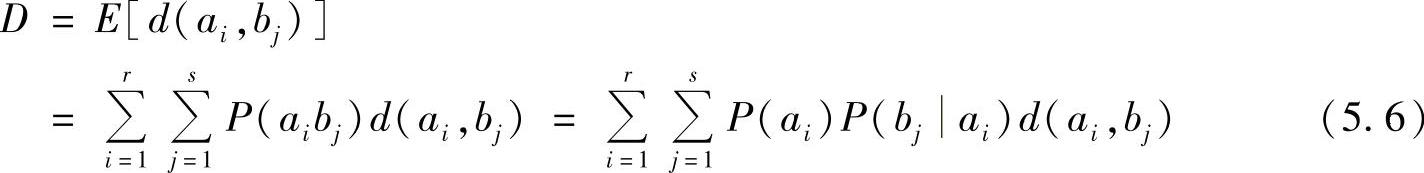
式中，P（a_i）是信源X的概率；P（a_ib_j）是信源X和信宿Y的联合概率；P（b_ja_i）是试验信道的转移概率。

由定义5.5知，平均失真度D是在X和Y的联合概率空间求平均。平均失真度已对信源和信道进行了统计平均，所以此值描述了某一信源在某一试验信道下的失真大小。

平均失真度D是信源的统计特性P（a_i）、试验信道转移特性P（b_ja_i）和失真度d（a_i，b_j）的函数。当失真度d（a_i，b_j）被确定、信源统计特性P（a_i）给定以后，平均失真度D就是试验信道转移概率P（b_ja_i）的函数。因此，改变信道的转移概率就可以改变平均失真度。

如果规定离散信源符号的平均失真度D′小于所允许的失真D，即

D′≤D （5.7）则D是允许失真的上界，并称式（5.7）为保真度准则。

平均失真度的引入给出了这样一种可能，即把能控制的允许的平均失真度作为对信道转移概率P（b_ja_i）的一种约束条件。在此约束条件下，求解试验信道的信息传输率I（X；Y）的最小值就有实用意义了，即在可以接受的失真范围内进行压缩。

以上是单符号信源的失真度和平均失真度。这些概念可以推广到长度为N的信源符号序列的失真函数。

设信源输出的N维符号序列为X=（X₁，X₂，…，X_N），其中随机分量X_i（i=1，2，…，N）的值域为符号集A：{a₁，a₂，…，a_r}，共有r^N个不同的N维信源符号序列；收信端的N维符号序列为Y=（Y₁，Y₂，…，Y_N），其中随机分量Y_i（i=1，2，…，N）的值域为符号集B：{b₁，b₂，…，b_s}，共有s^N个不同的N维接收符号序列。

定义5.6 设发送的N维序列为α_i=a_i1a_i2…a_iN，接收的N维序列为β_j=b_j1b_j2…b_jN，N维序列失真度定义为

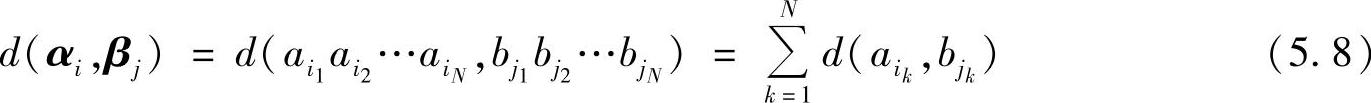
可以将r^N×s^N个非负的d（α_i，β_j）排列成矩阵形式，即

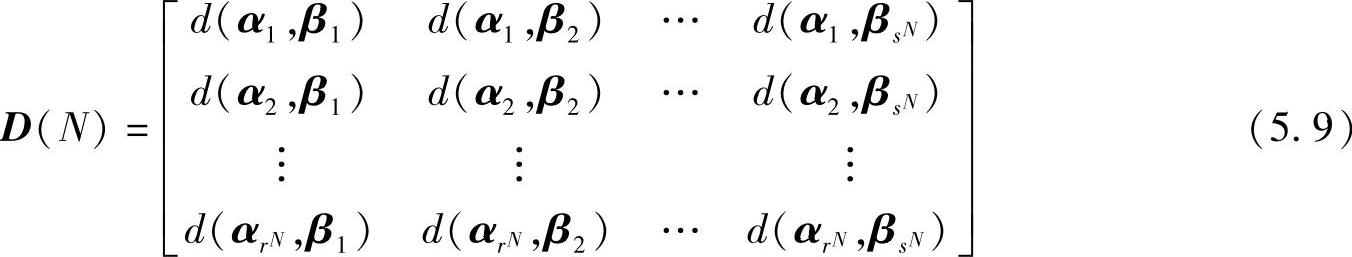
【例5.4】

假设信源输出序列X=（X₁，X₂，X₃），其分量的值域为A：{0，1}，经信道传输后的输出为Y=（Y₁，Y₂，Y₃），其分量的值域为B：{0，1}。失真函数使用Hamming失真函数，则由序列失真度定义可得

d（000，000）=d（0，0）+d（0，0）+d（0，0）=0

d（000，001）=d（0，0）+d（0，0）+d（0，1）=1同理可计算其他序列的失真度，并写成序列失真矩阵为

定义5.7 N维信源符号序列的平均失真度定义为序列失真度d（α_i，β_j）的数学期望，即

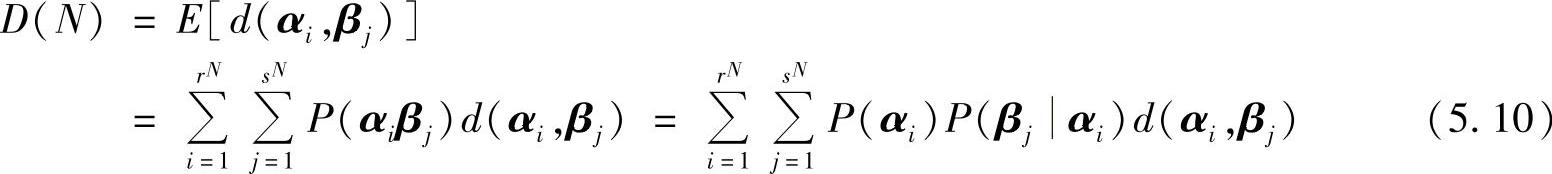
式中，P（α_i）是N维信源X的概率；P（α_iβ_j）是N维信源X和N维信宿Y的联合概率；P（β_jα_i）是N维试验信道的转移概率。

定义5.8 N维信源的平均失真度（单个符号的平均失真度）定义为

可以证明，当信源和信道都是无记忆时，有

式中，D_k是信源序列第k个分量的平均失真度。注意D_N和D_k表示的意义不同。

如果离散信源是平稳信源，信道又是平稳信道，则

即离散无记忆平稳信源通过离散无记忆平稳信道，其信源序列的平均失真度等于单个符号平均失真度的N倍。相应的保真度准则为

D′（N）≤ND （5.14）