LZW编码算法简介与优化

1984年韦尔奇（T.A.Welch）开发的LZW编码是LZ系列码中应用最广、变形最多的LZ算法，它的标识只有一项k，即指向字典的指针，这是它与LZ-77和LZ-78编码的一个主要不同点。为实现简化标识，它的编码思想与前述的算法有很大的不同。

LZ系列算法的共同点是分解输入流，使其成为长度各异的“短语”，并把它们存入短语字典，并给每个短语赋予一个码字（经常是短语的字典顺序号，这最简捷）。只要短语的码字长度短于短语的长度，就达到了压缩的目的。

而LZW编码算法则是先建立初始字典，再分解输入流为短语词条，这个短语若不在初始字典内，就将其存入字典，这些新词条和初始字典共同构成编码器的字典。而初始字典可以由信源符号集构成，每个符号是一个词条。更一般地，是将扩展的ASCII码存入初始字典，使其成为字典的前256项（0～255项）。这样的初始化字典，在应用中就足够大了。

LZW码的编码原理：先建立初始化字典，然后将待编码的输入数据流分解成短语词条。编码器要逐个输入字符，并累积串联成一个字符串，即短语I。若I是字典中已有的词条，就输入下一个字符x，形成新词条Ix。当I在字典内，而Ix不在字典内时，编码器首先输出指向字典内词条I的指针（即I的相应码字）；再将Ix作为新词条存入字典，并为其确定顺序号；然后把x赋值给I，当作新词条的首字符。重复上述过程，直到输入流都处理完为止。

下面通过举例来说明LZW编码过程。

【例4.25】（续例4.24）

信源符号集A：{a，b，c，d}，信源序列为aacdbbaaadcacbaaadccacbbbaadcbacba，对其进行LZW编码。

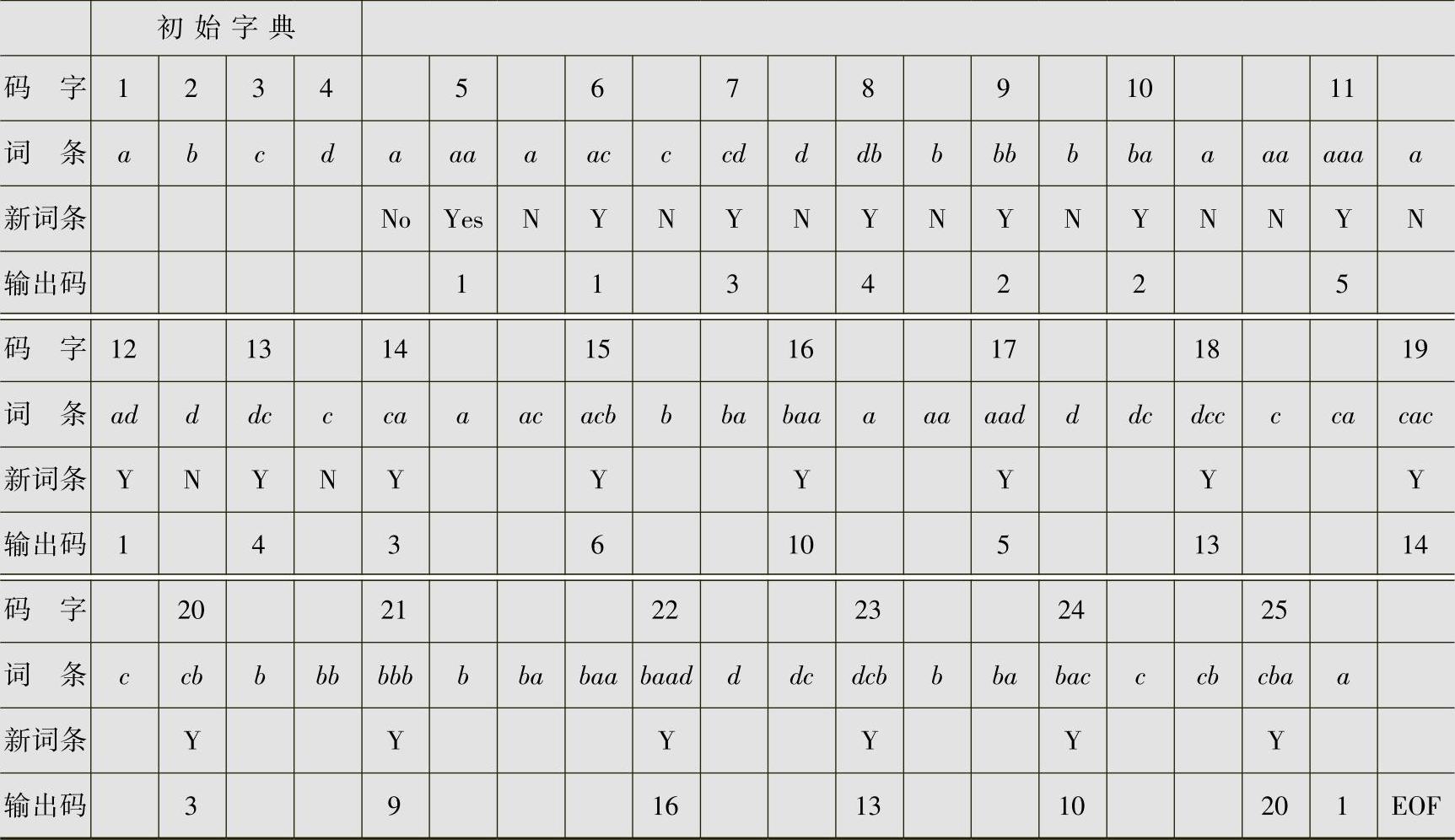
解 将信源符号a、b、c、d编码，其二元码字为a→00，b→01，c→10，d→11。其LZW编码的过程见表4.18。

先建初始化字典，此处只需将信源符号a、b、c、d预置为字典的前4项。

按编码原则，将首字符a预置为I，即I=a，搜索后知I在字典内，则继续输入序列第二项a，即有Ix=aa，搜索后知Ix不在字典内。则编码器先输出指向字典词条I=a的指针，即a相应的码字1，再把Ix=aa作为新词条存入字典，并编码得码字为5。再将x赋值给I，即此时I=a，当作新词条的首字符重复上述做法，得到编码表4.18。(www.xing528.com)

最后输出的LZW码字：1，1，3，4，2，2，5，1，4，3，6，10，5，13，14，3，9，16，13，10，20，1，EOF。式中EOF是End-of-File的缩写，是终止符号。

表4.18 例4.25的LZW编码过程

LZW码解码的第1步，输入第1个码字（即第1个指针），并从字典中取回一个词条I，并将I输出，同时将Ix存入解码字典中。但此时，x是未知的，x将是下一个从字典中读取的词条的首个字符。再输入下一个指针，又从字典中取回词条J，将其输出，并把J的首字符赋予上一步存入字典的词条Ix的x，则此时，Ix已完全确定。重复上述过程，则自动重建了译码表，并将译码输出。

同样地，字典的数据将采取多叉树结构，以利于数据管理和搜索加速。要注意到，在工程应用中，又出现各种LZW码的改进码，如LZMW码、LZAP码等。

LZ码和其他各类字典码是一种通用编码，编码方法不依赖信源的概率分布。这种编码方法不需要信源的统计特性，而且编码方法简单，编译码速度快，又能达到最佳压缩编码效率，因此得到了广泛应用。它已实现成为计算机UNIX操作系统中的标准文件压缩程序和个人计算机中ARC、RAR、ZIP等文件压缩程序。此算法可以将典型的ASCII文本文件压缩成原文件的一半以上，即压缩比为2或更大。此算法也容易用硬件实现，所以在文本文件压缩方面得到了广泛应用。

本章讨论了基于熵概念的无损压缩编码及其各种压缩算法。这些方法在实际工程技术中得到广泛的应用，如现在所用的各种图像格式，除BMP文件外，都用到这些无损压缩编码算法。又如广为人知的MP3音乐压缩格式中，也同样用了这些算法。这些方法都能使平均码长接近信源熵这个极限值。

通过最佳的信源编码虽然可以消除信源的冗余度，提高信息传输率，但结果却使码变得十分脆弱，经不起信道中噪声的干扰，容易造成译码错误。因此，必须进一步研究信息传输的抗干扰问题。