算术编码：一种高效的非分组编码方法

算术编码是20世纪80年代发展起来的一种高效无损编码方法。自1979年J.Rissanen和G.G.Langdon的论文“Arithmetic Coding（算术编码）”中提出了算术编码的系统方法之后，算术编码进入到实用阶段。如今，无论是计算机数据交换还是文本存储，以及视、音频数据压缩编码等，都应用了算术编码技术。

前面讨论的无失真编码建立在信源符号与码字一一对应的基础上。这种编码方法通常称为块码或分组码，此时信源符号一般应是多元的，且不考虑信源符号之间的相关性。如果要对最常见的二元序列进行编码，则需采用游程编码或合并信源符号等方法，把二元序列转换成多值符号，转换后这些多值符号之间的相关性也是不予考虑的。这就使信源编码的匹配原则不能充分满足，编码效率一般不高。

为了克服这种局限性，就需要跳出分组码的范畴。本小节要介绍的算术编码是一种非分组码。在算术编码中信源符号和码字不存在一一对应关系，它是一种从整个符号序列出发采用递推形式进行编码的方法。

算术编码的基本思路是从整个符号序列出发，计算信源序列的概率和累积概率，并用这些概率值将[0，1）区间分成互不重叠的小段，每段的长度等于某一信源序列的概率。再在段内取一个二进制小数，其长度可以与该序列的概率匹配，达到高效率编码的目的。这种方法与Shannon编码法有些类似，只是它们考虑的信源对象有所不同。Shannon码针对单个信源符号，而算术码针对信源符号序列。

1.累积概率的计算

先给出信源符号的累积概率。设信源为

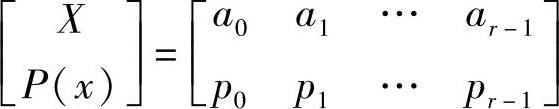
定义各符号的累积概率为

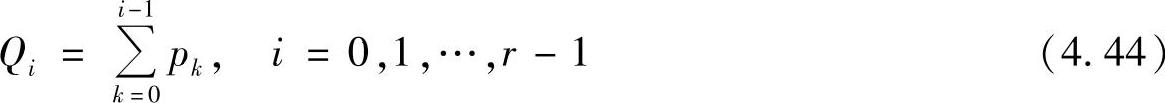
那么由式（4.44）可得Q₀=0，Q₁=p₀，Q₂=p₀+p₁=Q₁+p₁，…，Q_r-1=Q_r-2+p_r-2。

以r+1个点：0=Q₀，Q₁，Q₂，…，Q_r-1，1可以完整地分割区间[0，1），如图4.10所示。由图可见，r个互不重叠的区间[Q₀，Q₁），[Q₁，Q₂），…，[Q_r-1，1）的长度分别等于r个信源符号a₀，a₁，…，a_r-1的概率p₀，p1，…，p_r-1。如果将区间[Q_i-1，Q_i）与信源符号a_i-1建立一一对应关系，则用区间[Q_i-1，Q_i）内任意一点的取值就可以作为该区间对应的信源符号a_i-1的代码。只要该代码的长度与信源符号的概率相匹配，就可以得到高效率的信源编码。

图4.10 信源符号与对应的概率区间

再给出信源符号序列的累积概率。设信源X输出的N长序列为α=α₁α₂…α_N（α_i∈X），则总共有r^N种可能的序列。由于考虑的是整个符号序列，因而整页纸上的信息也许就是一个序列，所以序列长度N一般都很大。在实际中很难得到对应信源序列的概率和累积概率，一般从已知的信源符号概率P=（p₀，p₁，…，p_r-1）递推得到。

为了简单起见，先从独立二元序列开始讨论，再推广到一般情况。

设二元序列α=011。根据信源符号累积概率的定义，把它看作一个信源符号，则长度为3的二元序列一共有8个，按自然二进制数排列为000、001、010、011、100、101、110、111，相当于α₀，α₁，…，α₇。比如α=011对应α₃，其累积概率为

Q（α）=P（000）+P（001）+P（010） （4.45）

现在设想扩展序列长为4，则总序列数为16个。其中由α=011扩展的两个符号为0110或0111，也按自然二进制数排序，在0110前有6个序列，在0111前有7个序列，则可以计算累积概率如下：

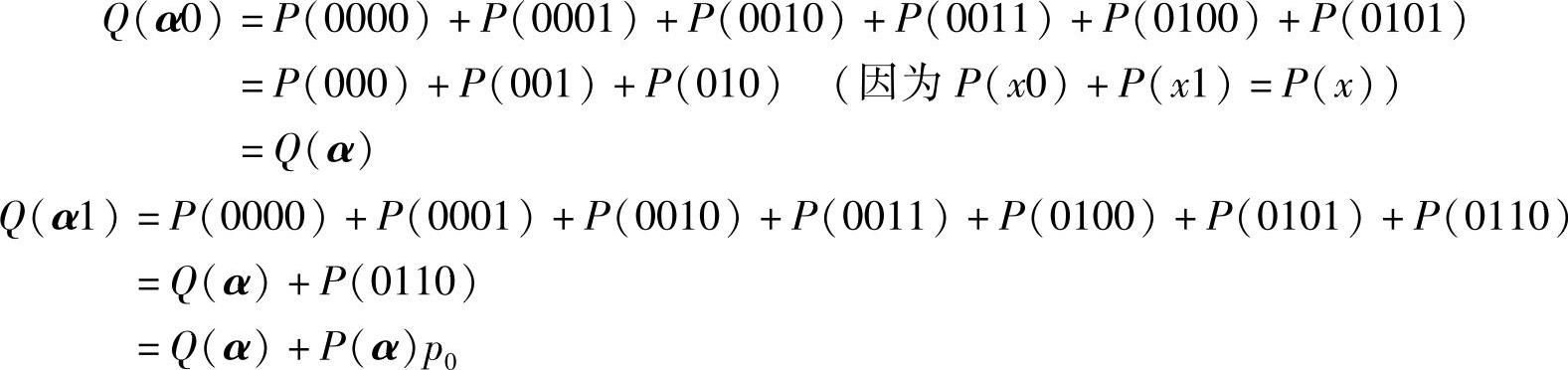
由于二元信源的累积概率为Q₀=0，Q₁=p₀，且有P（αr）=P（α）p_r，结合上面两式可得统一公式：

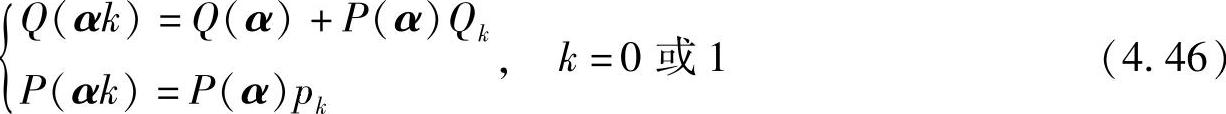
可以证明对于多元序列，有一般的递推关系：

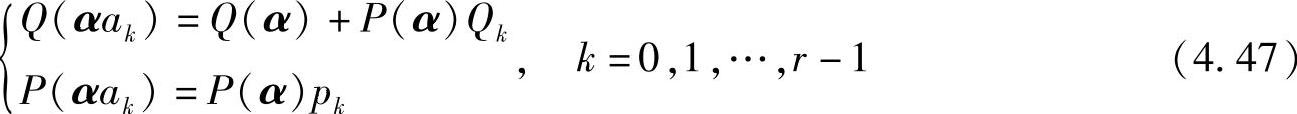
其中，α为一个多元序列；a_k为扩展字符；p_k为字符a_k的发生概率。

2.码区间分割与代码

从累积概率定义式（4.44）可以看到，计算得到的各个Q_i值实际上已完成了在半开区间[0，1）上的码区间分割，每个Q_i值就是分割线，而每个小区间的长度就是相对应的信源符号发生概率。因此，小区间内任一点的坐标值都可以代表该信源符号。特别地，坐标值的二进制数表示就可以当作相应的信源符号的码字。类似地，对于字符串α，码区间分割是根据式（4.46）或式（4.47）来进行的，其编码原理是一样的。下面讨论具体的编码过程。

首先讨论码长选择。根据出现概率大编短码、出现概率小编长码的原则，计算

式中，P（α）为字符串出现的概率；符号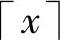表示大于等于x的最小整数。

然后，取累积概率Q（α）的二进制小数前l位作为码字，若有尾数，则进位到第l位。

例如，计算得Q（α）=0.10110001_{（二进制数）}，P（α）=1/7，则该字符序列α的算术码长为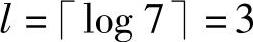，取Q（α）的前3位为0.101，尾数进位后为0.110，则α的算术码码字为110。

3.码字的唯一性

现在来讨论按上述规则编成的码字能否被唯一地译出其所代表的字符序列α。具体地说，就是码字w表示的小数值是否必定在区间[Q（α），Q（α）+P（α））内。为此要证明

Q（α）≤C＜Q（α）+P（α） （4.49）

首先，由于w取Q（α）前l位且尾数进位，显然有Q（α）≤C。

其次，由式（4.48）可知P（α）≥2^-l，因而有

Q（α）+P（α）≥Q（α）+2^-l

而2^-l表示二进制小数在小数点右边第l位为1的小数值，相当于当Q（α）有尾数时的进位值；因此有

C＜Q（α）+2^-l

这是因为规则是没有尾数时不进位，此时(www.xing528.com)

C=Q（α）＜Q（α）+2^-l

有尾数时进位，此时

C=Q（α）-尾数+2^-l＜Q（α）+2^-l

从而证明了C＜Q（α）+P（α）。

4.算术码的编码

实际编算术码时，用递推公式（4.47）可以逐位计算信源序列累积概率和信源序列概率，只要存储器容量允许，无论序列有多长，皆可以一直计算下去，直至序列结束。下面给出算术编码的计算步骤（设待编码信源序列为α₁α₂…α_N（α_i∈X））：

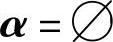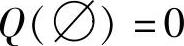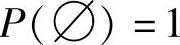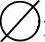1）初始化，，，i=1，表示空集。

2）输入信源符号α_i=a_k，计算Q（αa_k）=Q（α）+P（α）Q_k和P（αa_k）=P（α）p_k。

3）信源符号序列输入是否结束，若未结束，则i=i+1，转2）；否则，执行4）。

4）计算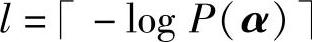，取二进制数的形式Q（α）的前l位作为信源序列α₁α₂…α_N的码字，若后面有尾数就进位到第l位。

【例4.20】

设二元独立信源，求信源序列10111101的算术编码。

解 信源符号的概率为p₀=0.25，p₁=0.75，累积概率为Q₀=0，Q₁=p₀=0.25，信源序列10111101算术编码的相关数据见表4.13。设，，表中数据的计算过程如下（黑体数字表示二进制小数）：

表4.13 例4.20的信源序列10111101的算术编码

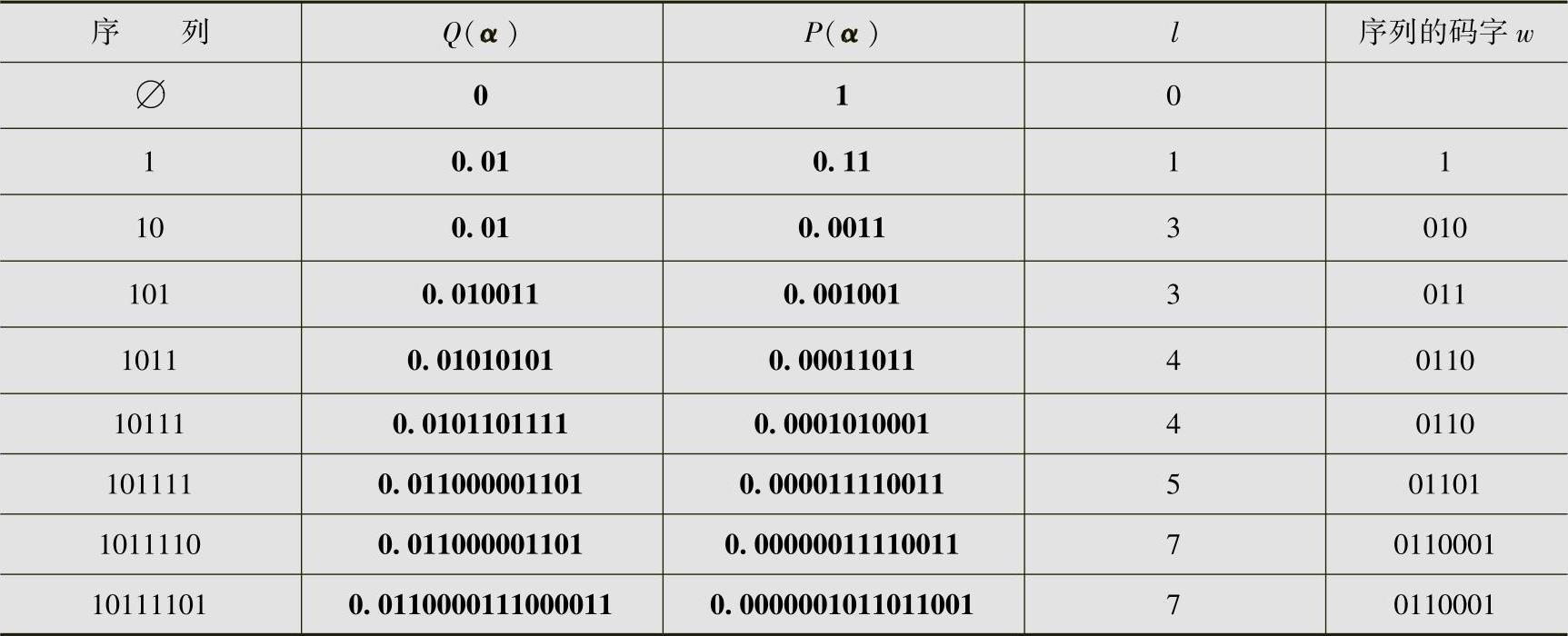
由此得序列10111101的编码为0110001。算术编码图解如图4.11所示。

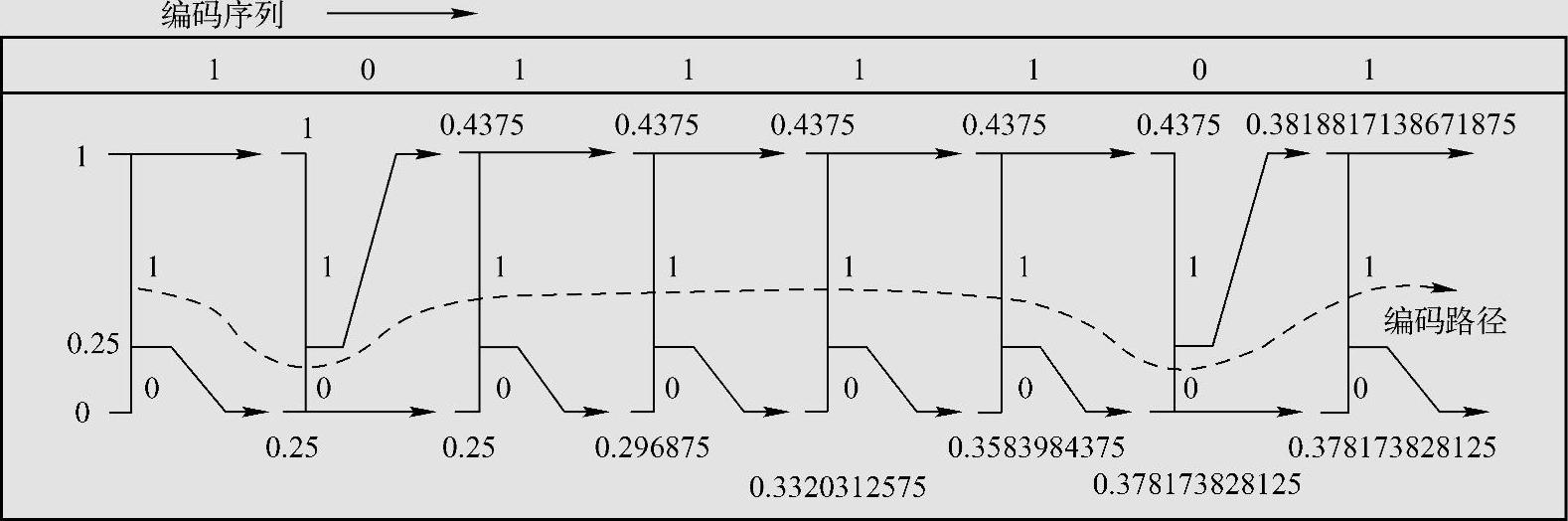
图4.11 算术编码过程区间宽度减小图解（例4.20）

【例4.21】

设四元无记忆信源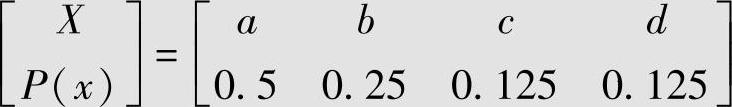，求信源序列abdac的算术编码。

解 信源符号的概率为p_a=0.5，p_b=0.25，p_c=p_d=0.125；累积概率为Q_a=0，Q_b=p_a=0.5，Q_c=Q_b+p_b=0.75，Q_d=Q_c+p_c=0.875；信源序列abdac的算术编码见表4.14。设，，表中数据的计算如下（黑体数字表示二进制小数）：

表4.14 信源序列abdac的算术编码

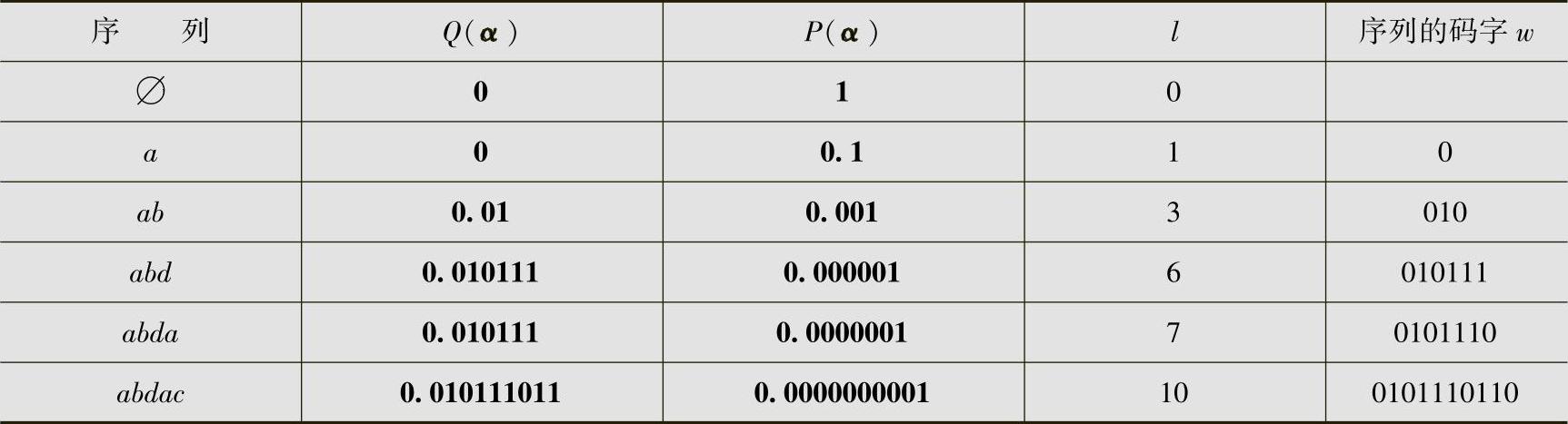
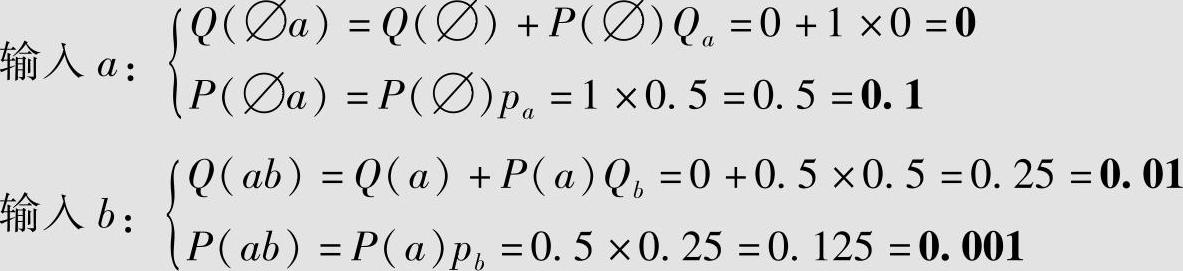
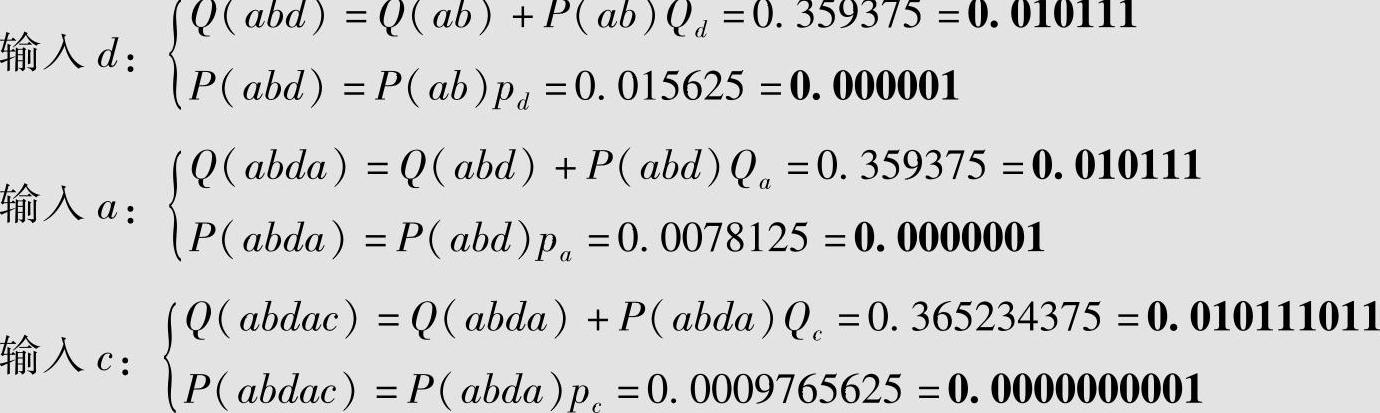
由此得序列abdac的编码为0101110110。算术编码图解如图4.12所示。

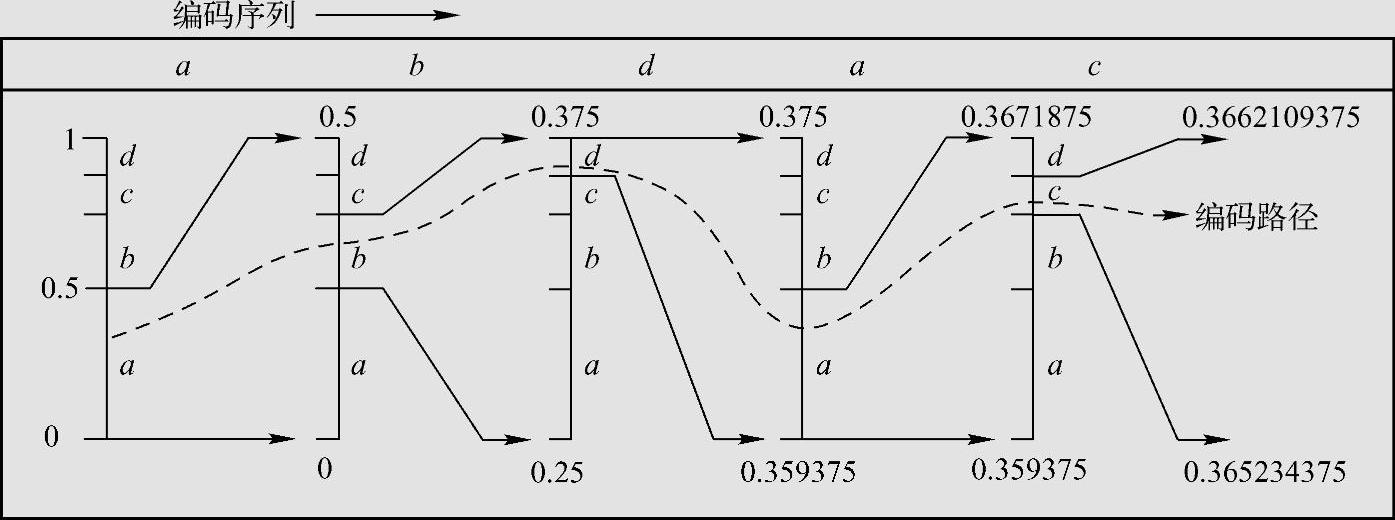
图4.12 算术编码过程区间宽度减小图解（例4.21）

5.算术码的译码

算术码的译码过程就是一系列的比较过程。由于接收到的编码w（一个小数）是信源序列累积概率的小数部分，可以用于恢复出数值C，且C值一定满足式（4.49）。

因此，算术码的译码就是每一步比较C-Q（α）与P（α）Q_k，其中，α为前面已经译出的序列串；P（α）是序列串α对应的宽度，也是序列串α的概率；Q（α）是序列串α的累积概率，即α对应区间的下限值；P（α）Q_k是此区间内下一个输入为符号a_k所占的区间宽度。

下面，以二元码为例，给出的译码规则如下：

若C-Q（α）＜P（α）Q₁，则译码输出符号为0；

若C-Q（α）＞P（α）Q₁，则译码输出符号为1。

例4.20和例4.21的编码结果的译码留作习题。

从性能上来看算术编码有许多优点，它所需的参数较少、编码效率高、编译码简单，不像Huffman码那样需要一个很大的码表。在实际实现时，常用自适应算术编码对输入的信源序列自适应地估计其概率分布。算术编码在图像数据压缩标准（如JPEG）和视频编码（如H.264）中得到了广泛的应用。