使用Huffman编码实现高效数据压缩

1952年赫夫曼（D.A.Huffman）提出了一种构造最佳码的方法，称之为Huffman码。Huffman码适用于多元独立信源，对于多元独立信源来说它是最佳码。它充分利用了信源概率分布的特性进行编码，是一种最佳的逐个符号的编码方法。

1.二元Huffman编码

二元Huffman码的编码步骤如下：

1）将r个信源符号按概率递减的次序排列：P（a₁）≥P（a₂）≥…≥P（a_r）。

2）用0和1码符号分别分配给概率最小的两个信源符号，并将这两个概率最小的信源符号合并成一个新符号，并用这两个最小概率之和作为新符号的概率，从而得到由r-1个符号组成的新信源X_r-1，称X_r-1为信源X=X_r的缩减信源。

3）把缩减信源X_r-1的信源符号按概率递减的次序排列，将其最后两个概率最小的信源符号合并成一个新符号，并分别用0和1码符号表示，形成r-2个符号的缩减信源X_r-2。

4）依次下去，直至缩减信源X₂只剩两个符号为止。将最后两个新符号分别用0和1码符号表示（最后两个符号的概率和为1）。然后从最后一级缩减信源开始，依编码路径由后向前返回，就得出各信源符号所对应的码符号序列，即得对应的码字。

下面给出两个具体的例子来说明这种编码方法。

【例4.15】（续例4.9）

对例4.9的离散无记忆信源进行二元Huffman编码。其二元Huffman编码过程见表4.7。平均码长为

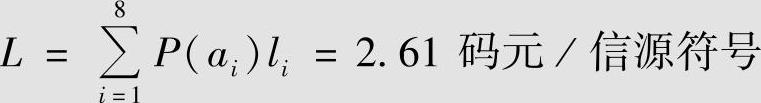
表4.7 例4.15的二元Huffman编码

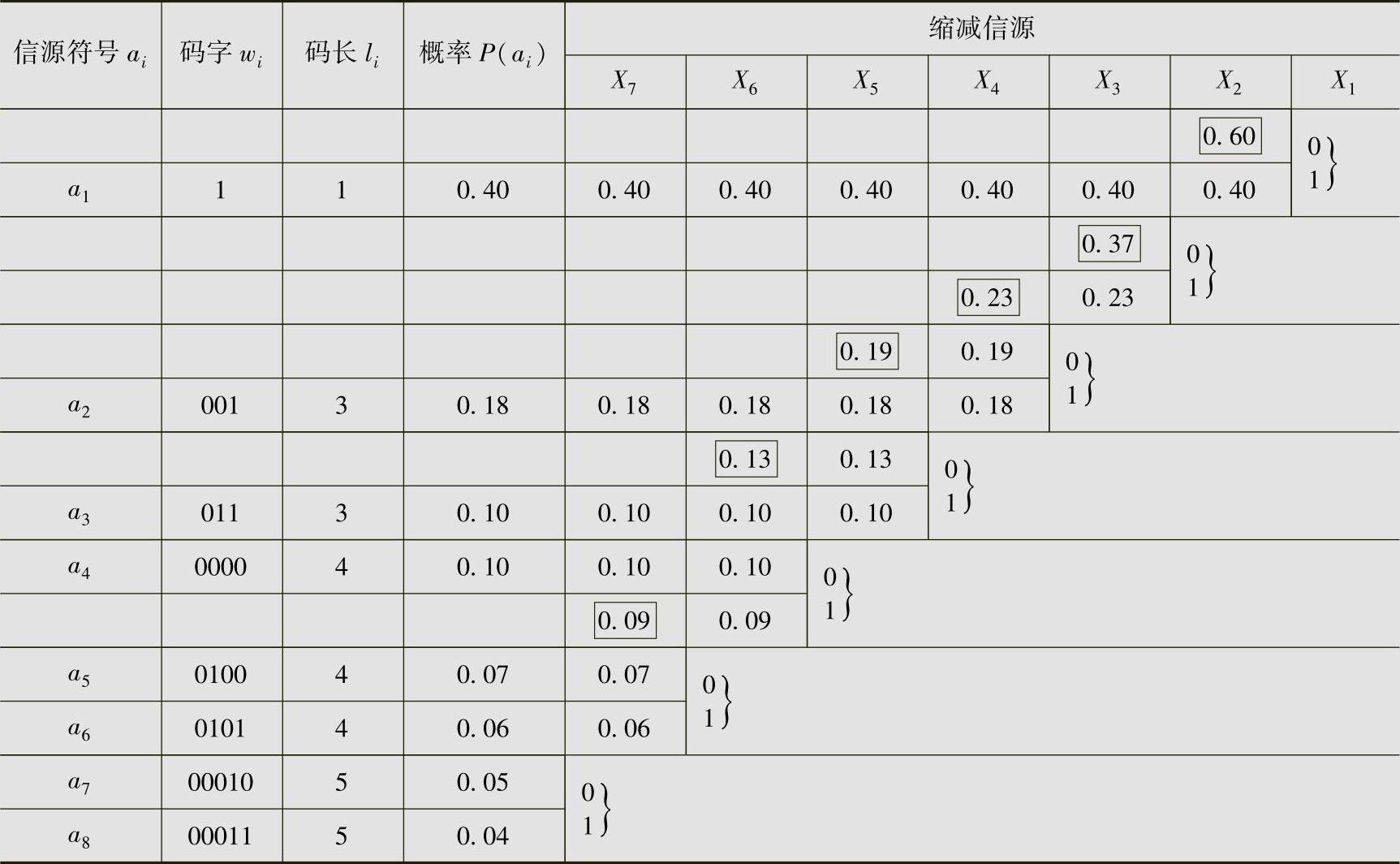
编码效率为

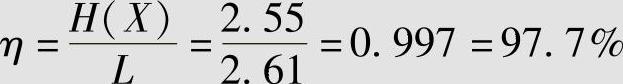
比较例4.15的Huffman码和例4.9的等长码，可见Huffman码在不需要对信源扩展时其效率就高达97.7%，而等长编码时要求对信源的扩展要达到1.63×10⁷时其效率才能达到90%，且有误码。因此，工程中广泛应用变长码进行信源压缩编码。

从例4.15（见表4.7）的编码过程中可以看出，Huffman码一定是即时码。因为这种编码方法得到的码字是非延长码。但必须注意，在表4.7中读取码字时，必须从后向前读取，否则所得码字不是即时码。

【例4.16】

设5个符号的离散无记忆信源为

对该信源进行二元Huffman编码。

解 该信源的熵为

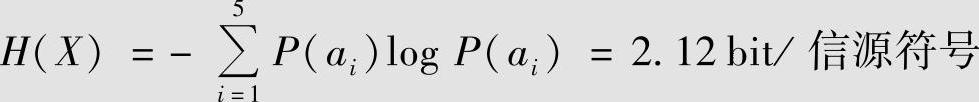
信源的两种二元Huffman编码过程见表4.8。第一种编码的平均码长为

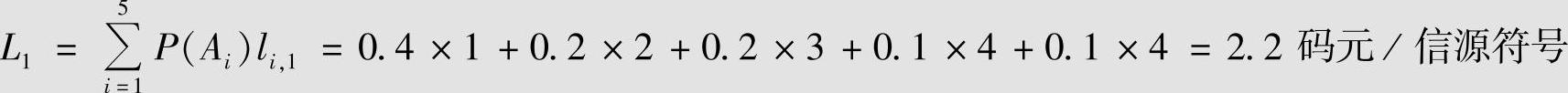
表4.8 例4.16的两种二元Huffman编码

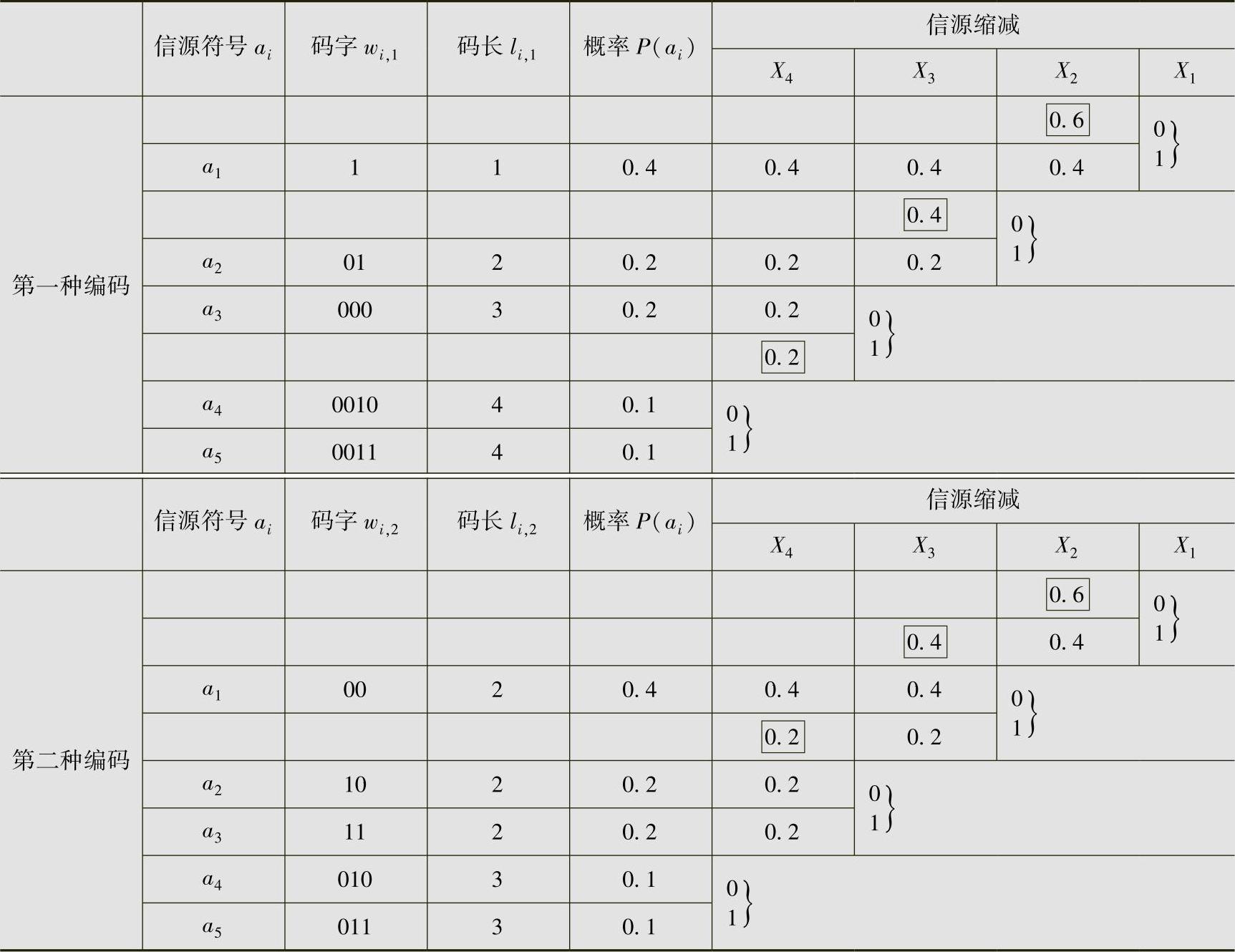
第二种编码的平均码长为

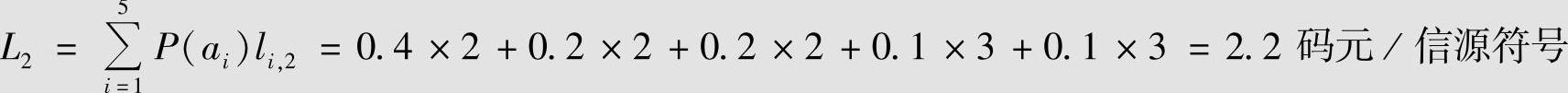
因此，两种码的编码效率相同，其值为

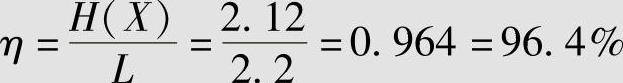
而两种码的编码长度的方差为

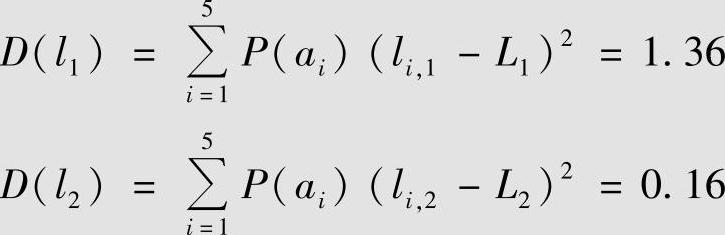
第二种编码方法的方差要小许多。对于有限长的不同信源序列，用第二种方法所编得的码序列长度变化较小。因此相对来说，选择第二种编码方法要更好。

由编码例子可见，Huffman编码得到的码并非是唯一的。这是因为以下两点：

1）每次对缩减信源最后两个概率最小的符号分配0和1码是可以任意的，所以可得到不同的编码。

2）若当缩减信源中缩减合并后的符号的概率与其他信源符号概率相同时，其不同的概率次序排列导致不同的编码结果，但它们的平均码长相同，方差不同。

通常，在Huffman编码过程中，当缩减信源的概率分布重新排列时，应使合并得来的概率和尽量处于最高的位置，这样可以使合并的元素重复编码次数减少，使短码得到充分利用。

从以上编码的实例中可以看出，Huffman码具有以下3个特点：

1）Huffman码的编码方法保证了概率大的符号对应短码，概率小的符号对应长码，而且短码得到充分利用。

2）每次缩减信源的最后两个码字总是最后一位码元不同，前面各位码元相同（二元编码情况）。

3）每次缩减信源的最长两个码字有相同的码长。

这三个特点保证了所得的Huffman码一定是最佳码。

2.s元Huffman编码(www.xing528.com)

上面讨论的是二元Huffman码，它的编码方法同样可以推广到s元编码中。不同的只是每次把s个符号（概率最小的）合并成一个新的信源符号，并分别用{0，1，…，s-1}等码元表示。

为了充分利用短码资源使平均码长最短，必须使最后一步的缩减信源有s个信源符号。因此对于s元编码，信源X的符号个数r必须满足

r=（s-1）θ+s （4.38）

式中，θ表示缩减的次数；s-1为每次缩减所减少的信源符号个数。

若r不满足式（4.38），可以增加t个信源符号a_r+1，a_r+2，…，a_r+t，令其概率为零，即P（a_r+1）=P（a_r+2）=…=P（a_r+t）=0，满足r+t=（s-1）θ+s。这样得到的s元Huffman码一定是最佳码。

【例4.17】（续例4.9和例4.15）

对例4.9的离散无记忆信源进行三元Huffman编码。其三元Huffman编码过程见表4.9，平均码长为

表4.9 例4.17的三元Huffman编码

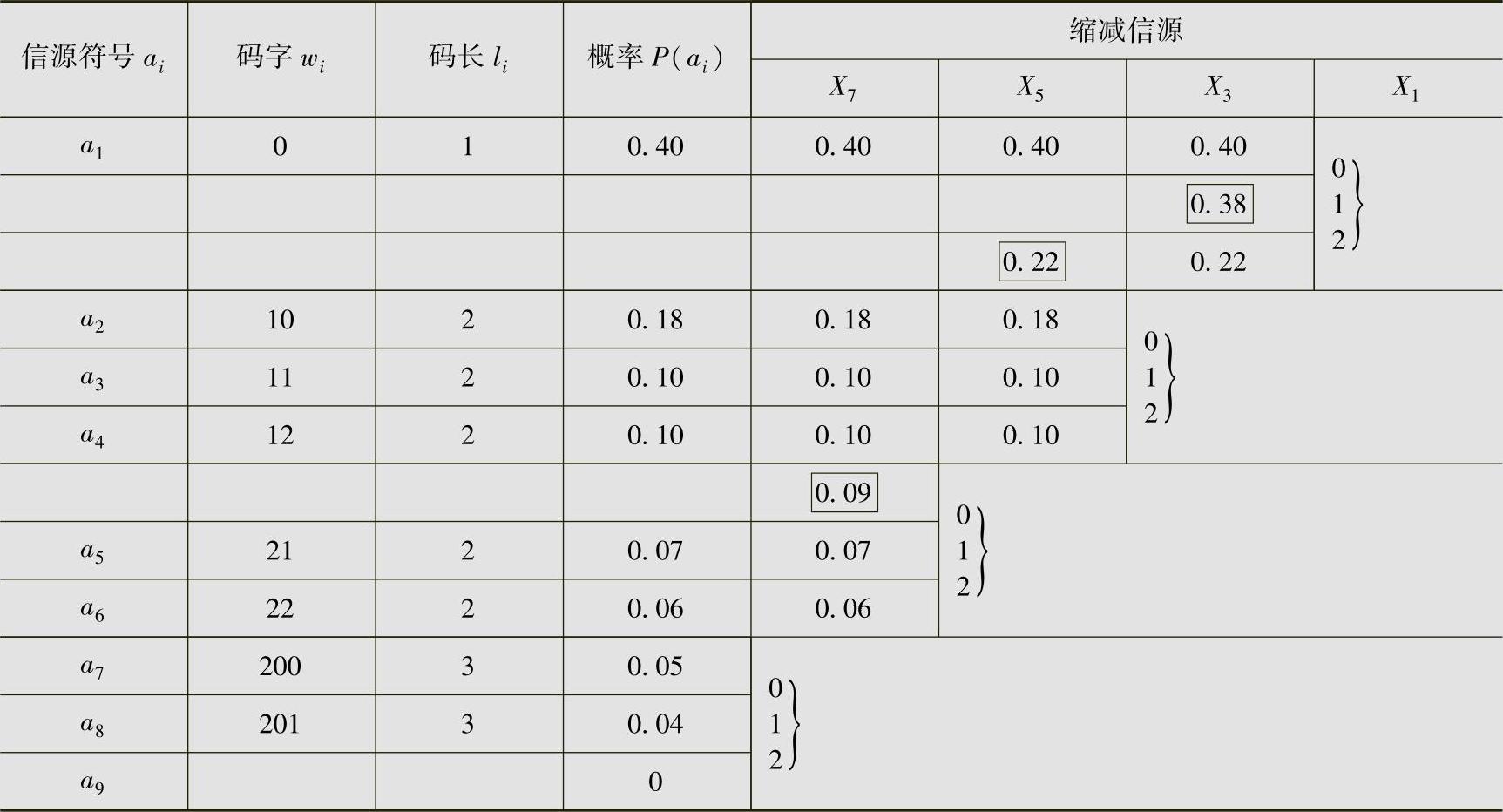
编码效率为

比较例4.17和例4.15的Huffman码可知，三元Huffman码的性能不如二元Huffman码的性能好。

3.Huffman码的最佳性

为了证明二元Huffman码是最佳二元码，首先证明最佳二元码应具有的一些性质，不失一般性，可以假设信源的概率分布按大小次序排列，即如p₁≥p₂≥…≥p_r，其对应的码长分别为l₁≤l₂≤…≤l_r。

定理4.10 对于给定分布的任何信源，存在一个最佳二元即时码（其平均码长最短），此码满足以下性质：

1）若p_j＞p_k，则l_j≤l_k。

2）两个最小概率的信源符号所对应的码字具有相同的码长。

3）两个最小概率的信源符号所对应的码字，除最后一位码元不同外，前面各位码元都相同。

证明1）若有即时码W′，其p_j＞p_k，而l_j′＞l_k′。交换这两个码字，得码W。交换后码W中l_j=l_k′，l_k=l_j′，其余l_i=l_i′（i≠j，k），则有

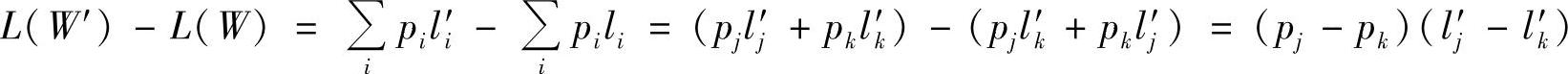
因为p_j＞p_k＞0，又因l_j′＞l_k′，所以L（W′）-L（W）≥0，即L（W）≤L（W′）。可见，交换后码W的平均码长变短，并满足p_j＞p_k，l_j≤l_k。所以，可以将码中所有码字进行交换，使其满足p₁≥p₂≥…≥p_r，而l₁≤l₂≤…≤l_r。这样得到的码，平均码长变最短。

2）由性质1）已知，两个最小概率的信源符号其码长最长，有p_r-1≥p_r，一定有l_r-1≤l_r。但若码W中l_r-1≠l_r，可以将此最长码字的最后几位截去，使l_r-1=l_r。这不但不影响即时码的前缀条件，而且使平均码长L（W）更为缩短，缩短了p_r（l_r-l_r-1）。

这样，两个最小概率的信源符号所对应码字的码长最长，而且相等。这时，所得码的平均码长最短。

3）根据性质1）和2），可以将一即时码W通过交换、截枝整理，得到平均码长为最短的码W。这时，两个最小概率的信源符号所对应的码字长度最长且相等。从树图角度来看，它们应是在同一节点伸出两枝叉的两个节点上（二元树）。若不在同一节点伸出两枝叉的两个节点上，一定在同一阶树枝的其他节点上（同一阶的节点码长相同）。否则，与性质1）、2）不一致了。这时，可以重新安排码字，使码字w_r-1和w_r在同一阶的同一节点伸出两枝叉的两个节点上。这样重新安排并不改变平均码长L（W）。因此得，这两个最小概率的信源符号所对应的码字，除最后一位码元不同外，前面各位码元都相同。

综合上述证得，若p₁≥p₂≥…≥p_r，则存在最佳即时码W，码长满足l₁≤l₂≤…≤l_r，而且码字w_r-1和w_r只有最后一位不同。

【证毕】

下面，证明Huffman码的最佳性。

定理4.11二元Huffman码一定是最佳即时码。即若W是Huffman码，W′是任意其他即时码，则有L（W）≤L（W′）。

证明由Huffman编码方法可知，每次缩减信源对应的码都满足定理4.10的性质。现设某一缩减信源X_j，得即时码W_j，它的平均码长为L_j。X_j中某一元素a_q是由前一缩减信源X_j+1中概率最小的两个符号合并而来的。设这两个符号为a_q0和a_q1，它们的概率分别为p_q0和p_q1，则X_j中符号a_q的概率p_q=p_q0+p_q1。根据Huffman编码方法得到X_j+1的码为W_j+1，它的平均码长为L_j+1。由于在码W_j+1中除了a_q0和a_q1两码字比a_q码字长一个二元数字外，其余码字长度都相同，因而L_j+1和L_j有以下关系：

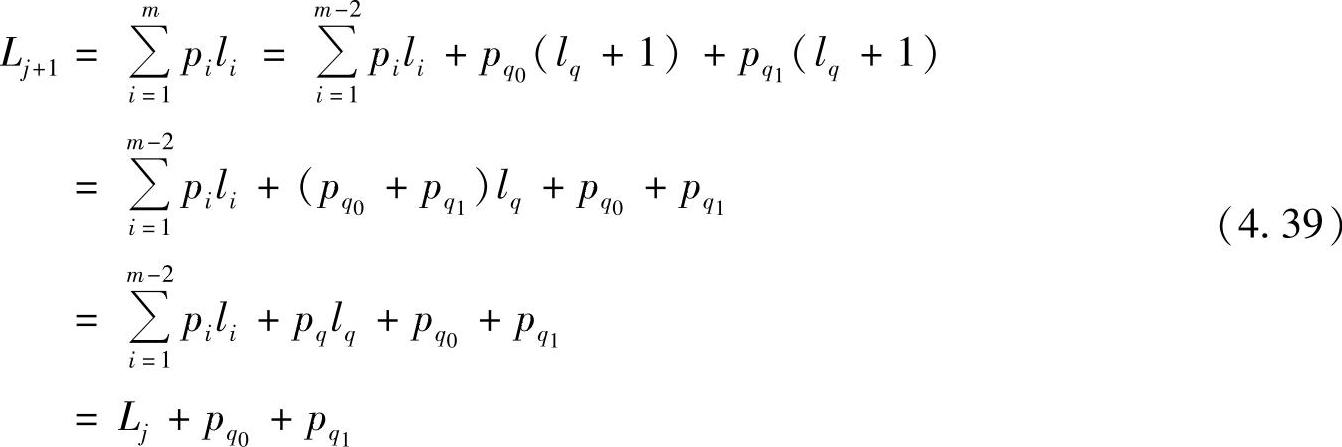
式中，假设信源X_j有m-1个元素，前一缩减信源X_j+1有m个元素。

由式（4.39）可知，缩减信源X_j和X_j+1的平均码长之差是一个与码长l_i无关的固定常数。所以，要求平均码长L_j+1最小，就是求平均码长L_j为最小。即对m-1个元素，求得l_i（i=1，2，…，m-1）使L_j为最小，得码W_j是信源X_j的最佳码，则此码长l_i，也使其前缩减信源的平均码长L_j+1为最小，码W_j+1是信源X_j+1的最佳码。

由Huffman编码方法一次一次缩减，最后一步得到的缩减信源X₂只有两个信源符号。分别编制一个码元，这样平均码长L₂=1为最短，所以码W₂一定是最佳码。

由于W₂（L₂=1）是最佳码，则由Huffman编码方法所得它前面一级缩减信源（最后第2级）X₃的即时码W₃也一定是最佳码，再前面一级缩减信源X₄的即时码也一定是最佳码。依次类推，信源X所得的Huffman码一定是最佳码。因此，证明Huffman编码方法一定是最佳编码方法。

【证毕】

上述证明定理4.10和定理4.11都是在二元码（s=2）的情况下进行的。同理，可以证明s元Huffman码一定也是最佳码。

因为Huffman码是在信源给定情况下的最佳码，所以其平均码长的界限为

H_s（X）≤L＜H_s（X）+1 （4.40）

对信源的N次扩展信源同样可以用Huffman编码方法。因为Huffman码是最佳码，所以编码后单个信源符号所编得的平均码长随N的增加很快接近于极限值——信源熵。

本节讨论了Huffman码，并且证明了Huffman码是最佳码。当N不很大时，它能使无失真编码的效率接近于1。但Huffman码是分组码（或块码），在实际应用时设备较复杂。

首先，每个信源符号所对应的码长不同。一般情况下，信源符号以恒速输出，信道也是恒速传输的。通过编码后，会造成编码输出每秒的比特数不是常量，因而不能直接由信道来传送。为了适应信道，必须增加缓冲寄存器，将编码输出暂存在缓冲器中，然后再由信道传输，使输入和输出的速率保持平衡。但当缓冲器存储量有限时，会出现缓冲器溢出或取空的现象。例如，当信源连续输出低概率的符号时，因为码长较长，有可能使缓冲器存不下而溢出。反之，当信源连续输出高概率符号时，有可能输出比特数小于信道中传输的比特数，以致使缓冲器取空。所以，一般来说，变长码只适用于有限长的信息传输。

其次，信源符号与码字之间不能用某种有规律的数学方法对应起来。在对信源进行Huffman编码后，形成一个Huffman码表，必须通过查表方法来进行编、译码。在信源存储与传输过程中必须首先存储与传输该Huffman码表，这就会影响实际信源的压缩效率。有时为了实用，常常先基于大量概率统计，事先建好Huffman码表。这样，编码时不需进行概率统计和建立码表；另外在接收端和发送端可以先固化建好的Huffman码表，传输时也不用传输码表。但当N增大时，信源符号数目增多，所需存储码表的容量增大，故使设备复杂化，同时也使编、译码时，查表搜索时间增大。尽管如此，Huffman方法还是一种较具体和有效的无失真信源编码的方法，它便于硬件实现和计算机上软件实现，所以仍应用于文件传真、语音处理和图像处理等数据压缩中。