理解Shannon编码的原理与应用

Shannon第一编码定理指出了平均码长与信源之间的关系，同时也指出了可以通过编码使平均码长达到极限值。根据Shannon第一编码定理，可以选择每个码字的长度l_i满足关系式

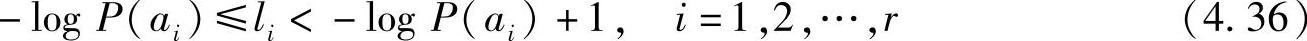
或

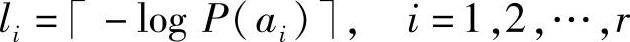
式中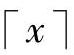，表示不小于x的整数。按式（4.36）选择的码长所构成的码称为Shannon码。Shannon码满足Kraft不等式，所以一定存在对应码字长度的唯一可译码。

一般情况下，按照Shannon编码方法编出来的码，其平均码长不是最短的，也即不是最佳码（紧致码）。只有当信源符号的概率分布使不等式（4.36）左边的等号成立时，编码效率才达到最高。

Shannon码的编码步骤如下：

1）将r个信源符号按概率递减的方式进行排列：P（a₁）≥P（a₂）≥…≥P（a_r）。

2）按式（4.36）计算出每个信源符号的码长：l₁，l₂，…，l_r。

3）计算第i个信源符号的累积概率：

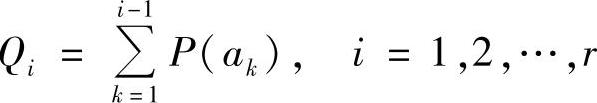
4）将累积概率Q_i用二进制数表示。

5）取Q_i对应二进制数的小数点后l_i位构成该信源符号的二元码字。

下面给出两个具体的例子来说明这种编码方法。

【例4.11】

设7个符号的离散无记忆信源为(www.xing528.com)

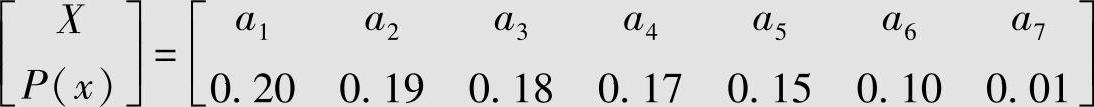
试对该信源进行Shannon编码。

解 计算信源符号a_i的自信息量-log P（a_i）、码长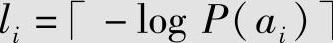、累积概率Q_i及其对应的二进制数，并取Q_i对应二进制数的小数点后l_i位构成a_i对应的码字w_i，见表4.4。

表4.4 例4.11的Shannon编码

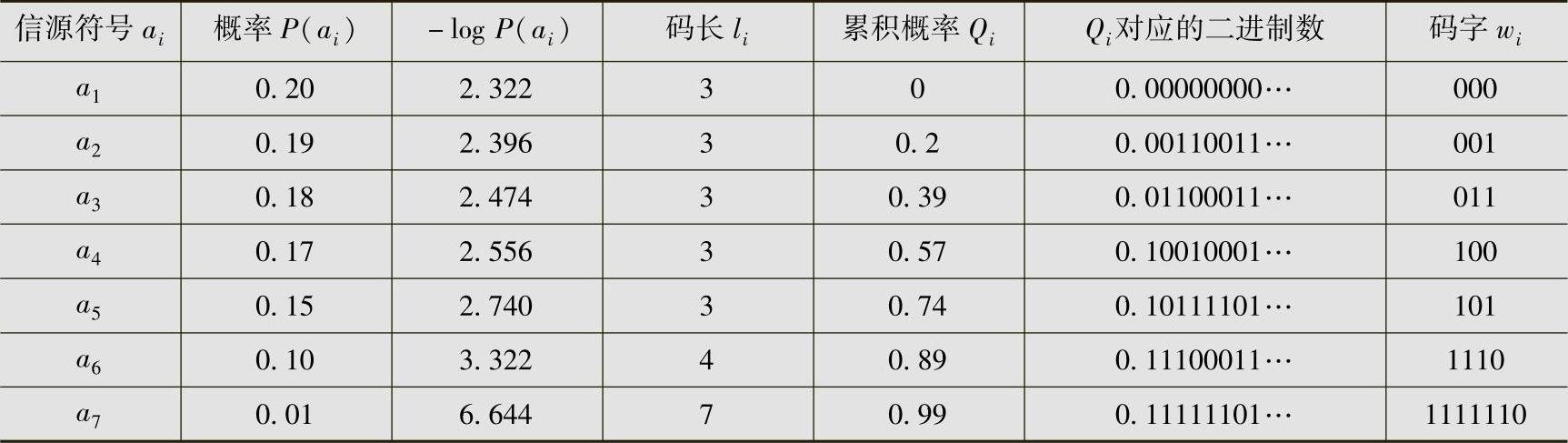
码的性能分析：此信源的熵为

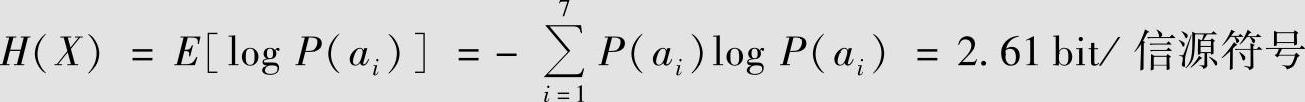
码的平均长度为

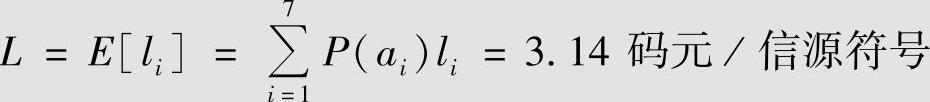
编码效率为

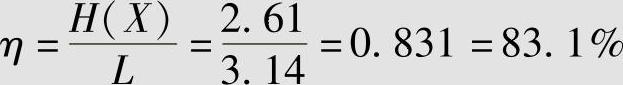
【例4.12】

信源X有3个信源符号，其信源概率为0.5、0.4、0.1，按Shannon编码对该信源进行编码所得的码长应为1、2、4，对应的码字为（0，10，1110），其平均码长为L=1.7码元/信源符号，信源的熵H（X）=1.36 bit/信源符号。因此，该码的编码效率η=0.801。

实际上，观察本例信源的概率分布，可以构造出一个码长更短的码0，10，11，显然它也是唯一可译码，但其平均码长为L=1.5码元/信源符号，编码效率η=0.907。

例4.12说明，Shannon编码的剩余度较大，实用性不强，但它是根据Shannon第一编码定理直接得出的，因此具有重要的理论意义，而且Shannon编码也是后面要介绍的算术编码的基础。