变长信源编码定理详解

定理4.6 若一个离散无记忆信源熵为H（X），每个信源符号用s进制码元进行变长编码，则总可以找到一种无失真编码方法，构成唯一可译码，使其平均码长L满足

证明 先证明下界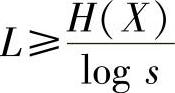。将下界条件改写为

H（X）-Llog s≤0

根据定义有

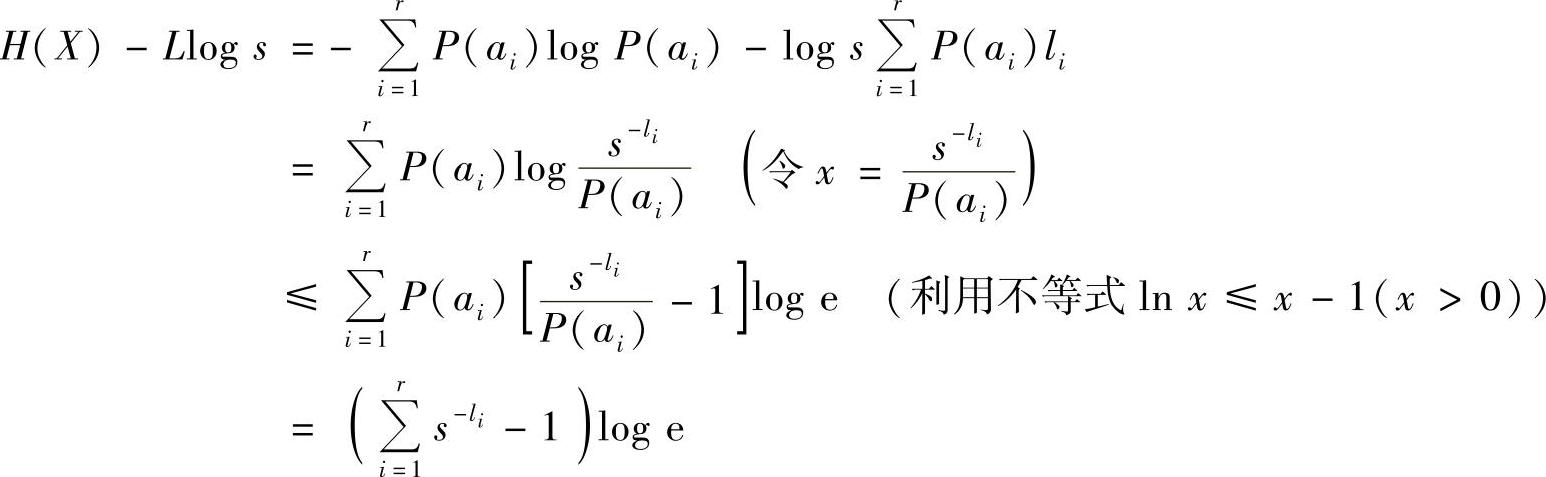
因为总可以找到一种唯一可译码，它的码长满足Kraft不等式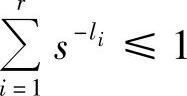，所以

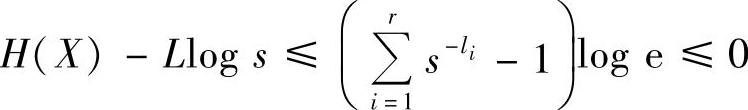
于是证得

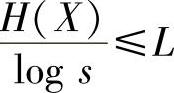
由证明过程知，上述等式成立的充要条件是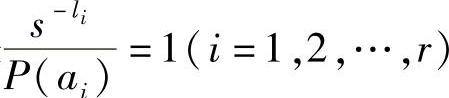，即

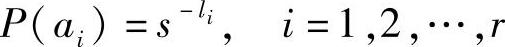
取对数，得

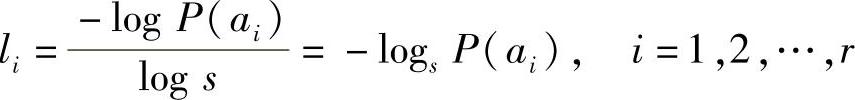
可见，只有当能够选择每个码长l_i等于-log_sP（a_i）时，平均码长L才能达到下界值。由于l_i必须是正整数，所以-log_sP（a_i）也必须是正整数。也就是说，当等式成立时每个信源符号的概率P（a_i）必须呈现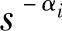的形式（α_i是正整数）。如果满足这个条件则只要选择l_i=αi（i=1，2，…，r），然后根据这些码长，就可以按照树图法构造出一种唯一可译码，而且所得的码一定是最佳码。再证明上界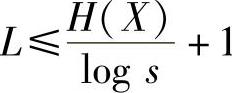成立。把信源符号概率P（a_i）表示为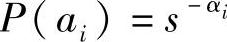（α_i是正数，但不一定是整数）。然后选取信源符号a_i的编码长度l_i满足

α_i≤l_i＜α_i+1，i=1，2，…，r （4.24）

由P（a_i）=s^-αi，结合式（4.24）中α_i≤l_i，可以推得P（a_i）≥s^-li，将此式两边对i求和，得

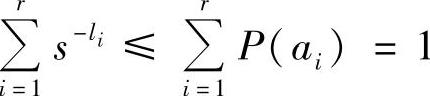
可见，这样选择的码长满足Kraft不等式，可以构造出唯一可译码。但所得码并不一定是最佳码。由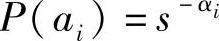，结合式（4.24）右边不等式l_i＜α_i+1，可以推得

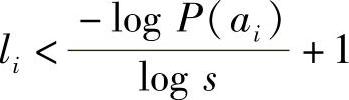
上式两边乘以P（a_i），并对i求和，得

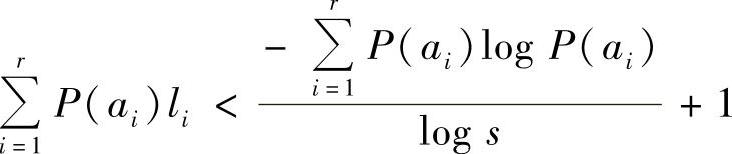
因而，得

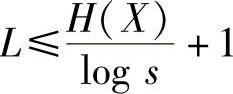
由此证明得到，平均码长小于上界的唯一可译码存在。

【证毕】

需要说明的是，式（4.23）中熵H（X）与logs的信息量单位必须一致。若熵以s元为单位，则式（4.23）可以写成

H_s（X）≤L≤H_s（X）+1 （4.25）

式中，。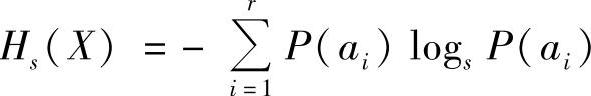

从单位来看，在式（4.23）中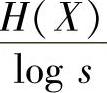的单位是码符号/信源符号，它与平均码长L的单位是一致的。在式（4.25）中似乎H_s（X）单位应是s元单位/信源符号，但因为现在每个s元码符号携带1个s元单位信息量，所以实际上，式（4.25）中H_s（X）的单位仍是码符号/信源符号，与平均码长的单位仍是一致的。

定理4.6表明，码字的平均长度L不能小于极限值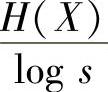，否则唯一可译码不存在。同时又给出了平均码长的上界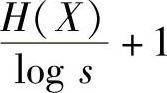。但并不是说大于上界不能构成唯一可译码，而是希望平均码长L尽可能短。定理说明当平均码长小于上界时，唯一可译码也存在。因此定理4.6给出了最佳码的最短平均码长，并指出这个最短的平均码长与信源熵是有关的。

另外还可以看到这个极限值与等长信源编码定理4.5中的极限值是一致的。

定理4.7（无失真变长信源编码定理（Shannon第一编码定理）） 设离散无记忆信源X的熵为H（X），它的N次扩展信源X^N的熵为H（X^N）。码符号集为Y（有s个符号）。对信源X^N进行编码，总可以找到一种编码方法，构成唯一可译码，使信源X中每个信源符号所需的平均码长满足

或者

当N→∞时，则得

式中，L_N是无记忆扩展信源X^N中每个符号α_i的平均码长，即

其中，l_i是α_i所对应的码字长度。

可见，L_N/N仍是信源X中每一单个信源符号所需的平均码长。这里要注意L_N/N和L的区别。它们两者都是每个信源符号所需的码符号的平均数，但是，L_N/N的含义是，为了得到这个平均值，不是对单个信源符号a_i进行编码，而是对N个信源符号的序列α_i进行编码。

显然，定理4.6是定理4.7在N=1时的特殊情况。

证明 将X^N视为一个新的离散无记忆信源，应用定理4.6得

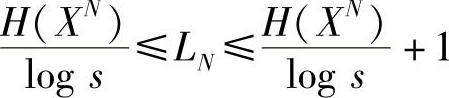
由第2章可知，N次无记忆扩展信源X^N的熵是信源X的熵的N倍，即H（X^N）=NH（X），将

该式代入上式，得

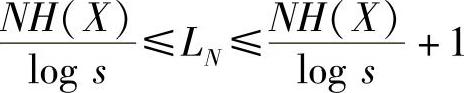
两边除以N，即得

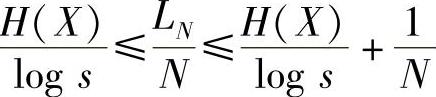
显然，当N→∞时，有

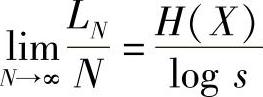
【证毕】

将定理4.7的结论推广到平稳有记忆信源，便有

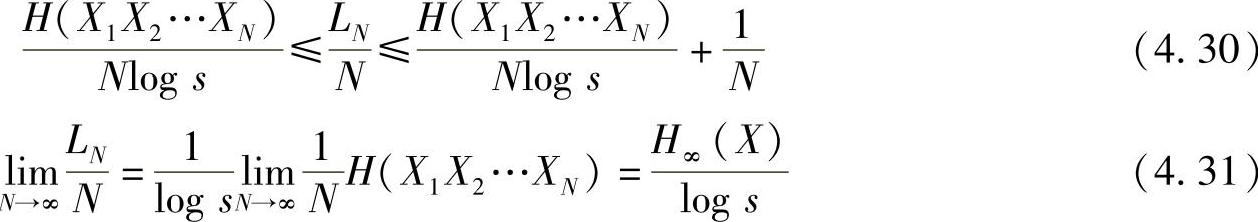
式中，H_∞（X）为平稳有记忆信源的极限熵（极限熵与log s的信息量单位必须一致）。

对于马尔可夫信源，式（4.30）和式（4.31）仍适用，只是式（4.31）中H_∞（X）应为马尔可夫信源的极限熵，公式证明可以参阅参考文献[29]中题解5.3。

定理4.7是Shannon信息论的主要定理之一。定理指出，要做到无失真的信源编码，每个信源符号平均所需最少的s元码元数就是信源的熵值（以s元信息量单位测度）。若编码的平均码长小于信源的熵值，则唯一可译码不存在，在译码或反变换时必然要带来失真或差错。同时定理还指出，通过对扩展信源进行变长编码，当N→∞时，平均码长L_N/N可以达到这个极限值。可见，信源的信息熵是无失真信源压缩的极限值。也可以认为，信源的信息熵（H（X）或H_∞（X））是描述信源每个符号平均所需最少的比特数。

再来观察定理4.7。若改写式（4.26），可得(https://www.xing528.com)

式中，（L_N/N）log s就是编码后平均每个信源符号能载荷的最大信息量，即变长信源编码后信源的信息传输率R=（L_N/N）log s。比较式（4.19）和式（4.32）可知，等长编码和变长编码的信息传输率的理论极限是一致的。有时，Shannon第一编码定理也可以陈述为：

定理4.8（精练的Shannon第一编码定理）若R＞H（X），就存在唯一可译变长编码；若R＜H（X），唯一可译变长码不存在，不能实现无失真的信源编码。

若从信道角度看，信道的信息传输率（码率）为

因为

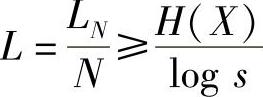
所以，可得编码后的信道的信息传输率为

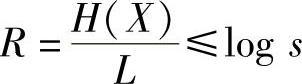
当平均码长L达到极限值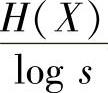时，上式等号成立，即

R=log s bit/码符号 （4.33）

由此可见，这时信道的信息传输率等于无噪无损信道的信道容量C，信道的信息传输效率最高。因此，无失真信源编码的实质就是对离散信源进行适当的变换，使变换后新的码符号信源（无噪无损信道的输入信源）尽可能为等概率分布，以使新信源的每个码符号平均所含的信息量达到最大，从而使信道的信息传输率R达到信道容量C，实现信源与信道理想的统计匹配。这也就是Shannon第一编码定理的物理意义。所以，无失真信源编码实质上就是无噪信道编码问题。

因此，无失真信源编码定理通常又称为无噪信道编码定理。此定理可以表述为：

定理4.9 若信道的信息传输率R不大于信道容量C，总能对信源的输出进行适当的编码，使得在无噪无损信道上能无差错地以最大信息传输率C传输信息；但要使信道的信息传输率R大于C，而无差错地传输信息则是不可能的。

由定理4.9可知，信道容量C是无噪信道无差错传输的最大信息传输率。

为了衡量各种编码距极限压缩值的情况，定义变长码的编码效率的概念。设对信源X进行编码所得到的平均码长为L，因为L一定大于或者等于H_s（X），所以变长编码的效率为平均码长L与极限值之比，一般对于有记忆信源有

对于无记忆信源有

其中，L=L_N/N。

η一定是小于或等于1的数。对同一信源来说，若码的平均码长L越短，越接近极限值H_s（X），信道的信息传输率就越高，就越接近无噪无损信道容量，这时η也越接近于1，所以可以用码的效率η来衡量各种编码的优劣。

另外，为了衡量各种编码与最佳码的差距，定义码的冗余度的概念。

定义4.13 码的冗余度定义为。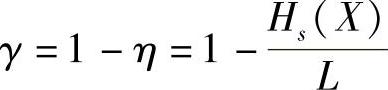

在二元无噪无损信道中s=2，所以H_s（X）=H（X），式（4.35）为

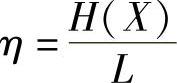
所以，在二元无噪无损信道中信道的信息传输率为

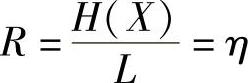
注意，R与η的数值相同，单位不同，其中η是个无单位的比值。为此，在二元信道中可以直接用编码的效率来衡量编码后信道的信息传输率是否提高了。当η=1时，即R=1 bit/码符号，达到了二元无噪无损信道的信道容量，编码效率最高，码冗余度为零。

【例4.10】

离散无记忆信源为

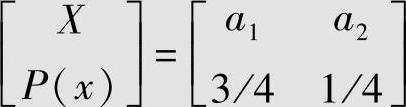
信源X的信息熵H（X）和自信息方差D[I（a_i）]分别为

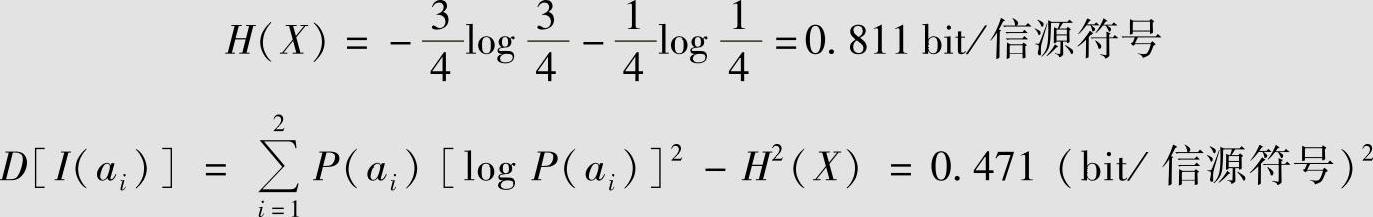
用二元码符号{0，1}来构造一个即时码：a₁→0，a₂→1。这时平均码长L=1（二元码符号/信源符号），编码的效率为

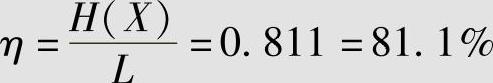
信道信息传输率为

R=0.811 bit/二元码符号

为了提高传输效率，根据Shannon第一编码定理的概念，可以对无记忆信源X的二次扩展信源X²进行编码。给出扩展信源X²及其某一个即时码，见表4.3。

表4.3 扩展信源X²的编码表

这个码的平均长度为

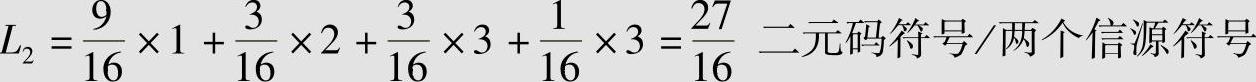
得信源X中每一单个符号的平均码长为

其编码效率为

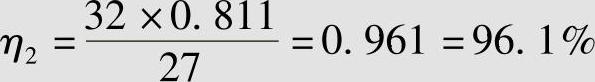
得R₂=0.961 bit/二元码符号。可见编码复杂了一些，但信息传输率有了提高。

用同样方法可以进一步对信源X的3次和4次扩展信源进行编码，并求出其编码效率为

η₃=0.985=98.5%

η₄=0.991=99.1%

这时信道的信息传输率分别为

R₃=0.985 bit/二元码符号

R₄=0.991 bit/二元码符号

若对信源进行等长编码，要求编码效率达到η=96%时，允许错误概率δ≤10^-5，由式（4.22）得需要的等长编码的长度N为

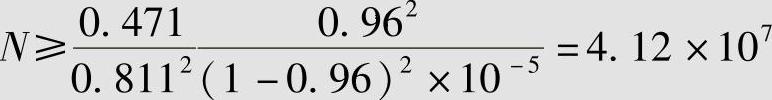
由例4.10可以看出，随着扩展信源次数的增加，变长编码的编码效率也在增加，并越来越接近于1，编码后信道的信息传输率R也越来越接近于无噪无损二元对称信道的信道容量C=1 bit/二元码符号，达到信源与信道匹配，使信道得到充分利用。通常，对信源进行至多5～7次扩展，其编码效率应能达到很高的水平。

此外，由例4.10还可以看出，当要求编码效率为96%时，等长码要求编码长度N≥4.12×10⁷，而无失真的变长码只需对二次扩展信源（N=2）进行编码就能达到96%以上的编码效率。

显然，变长编码的性能优于等长编码，所以变长码在实际应用中更具价值。