等长信源编码定理及其应用

定理4.5（等长信源编码定理）一个熵为H（X）的离散无记忆信源X，若对信源长为N的符号序列进行等长编码，设码字是从s个字母的码符号集中，选取l个码元组成。对于任意ε＞0，只要满足

则当N足够大时，可以实现几乎无失真编码，即译码错误概率能为任意小。反之，若

则不可能实现无失真编码，而当N足够大时，译码错误概率近似等于1。

定理证明的基本思路是，把离散无记忆信源的N次扩展信源划分成两个互补的集合。当N很大时，可以做到一个集合中元素较少但包含的都是经常出现的信源序列，而且这个集合出现的概率接近于1；另一个集合中虽包含的元素较多，但总的出现概率极小，趋于零。那么，对高概率集中的信源序列进行编码，而将低概率中的信源序列舍弃，不编码。这样，所需的平均码长可以减少，而所引起的错误概率却很小，且当N趋于无穷时错误概率趋于零。因此，只要知道高概率集中信源序列个数的上、下限，就可证得所需平均码长的上、下限。

定理4.5的证明可以参见文献[4]。定理4.5是在平稳无记忆离散信源的条件下论证的。但它同样适合于平稳有记忆信源，只是要求有记忆信源的极限熵H_∞（X）和极限方差σ²_∞（X）存在即可。对于平稳有记忆信源，式（4.15）和式（4.16）中H（X）应改为极限熵H_∞（X）。

当二元编码时，s=2，式（4.15）成为

可见，定理4.5给出了等长编码时平均每个信源符号所需的二元码符号的理论极限，这极限值由信源熵H（X）或H_∞（X）决定。

比较式（4.5）和式（4.17）可知，当信源符号具有等概率分布时，两式完全一致。但一般情况下，信源符号并非等概率分布，而且符号之间有很强的关联性，故信源的熵H∞（X）（极限熵）将大大小于log r。根据定理4.5可知，这时在等长编码中每个信源符号平均所需的二元码符号可以大大减少，从而使编码效率提高。

仍以英文电报符号为例，由第2章的讨论得知英文信源的极限熵H_∞（X）≈1.4 bit/信源符号，因此由式（4.17）得

此式表示平均每个英文信源符号只需近似用1.4个二元符号来编码，这比前面讨论的需要5位二元符号减少了许多。这样，平均每个二元符号载荷的信息将接近极大值1 bit，所以提高了信息传输效率。

定理4.5中的条件式（4.15）可以改写成

llog s＞NH（X） （4.18）

式（4.18）左边表示等长编码中每组l个码元可以携带的最大信息量为llog s，右边表示N个信源符号序列平均携带的信息量为NH（X）。所以，等长编码定理表明：只要码字传输的信息量大于信源序列携带的信息量，总可以实现几乎无失真编码。

等长编码的每一个码字的长度皆为l，其平均码长L=l。若用l长s个字母对信源长为N的符号序列进行等长编码，平均每个编码码元携带的信息量，即信息传输率（编码速率）为(www.xing528.com)

这样，定理4.5可以表述为，若R≥H（X）+ε，则可以实现无失真传输。

由定义4.12知等长编码的编码效率为

由式（4.20）知编码效率η≤1。此外，由定理4.5还可知，最佳等长编码的效率为

也就是说，最佳等长编码的效率可以接近于1。

由式（该式的证明请参见文献[15]）可知，当方差D[I（a_i）]和ε均为定值时，只要N足够大，错误概率p_ε就可以小于任意正数δ。可得，当允许错误概率小于δ，即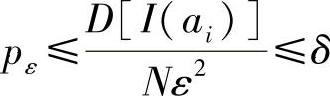时，信源序列长度N必满足

式（4.22）给定了在已知方差D[I（a_i）]和信源熵H（X）的条件下，信源序列长度N与最佳编码效率η和允许错误概率p_ε的关系。显然，当错误概率越小，编码效率又越高，则信源序列长度N必须越长。在实际情况下，要实现几乎无失真的等长编码，N需要的长度将会大到难以实现的程度。现举例说明如下：

【例4.9】

离散无记忆信源为

如果对信源符号采用等长二元编码，要求编码效率η=90%，允许错误概率δ≤10^-6，试确定其信源序列长度。

解 信源X的信息熵H（X）和自信息方差D[I（a_i）]分别为

将相关参数代入式（4.22）得信源符号联合编码长度为

由例4.9可见，在差错率和编码效率要求并不十分苛刻的条件下，就需要对信源进行极长的联合编码，这显然是不现实的。为提高编码有效性需要付出很大的代价。因此，一般来说，当N有限时，高传输效率的等长码往往要引入一定的失真和错误，为了解决这一个问题，人们就很自然地转向于对变长编码的研究。