信息论基础及应用：等长编码

若要实现无失真的编码，不但要求信源符号a_i（i=1，2，…，r）与码字w_i（i=1，2，…，r）一一对应，而且要求码符号序列的反变换也是唯一的。也就是说，所编的码必须是唯一可译码。否则，所编的码不具有唯一可译码性，就会引起译码带来的错误与失真。

对于等长编码，若等长码是非奇异码，则它的任意有限长N次扩展码一定也是非奇异码。因此，等长非奇异码一定是唯一可译码。

若对信源X：{a₁，a₂，…，a_r}进行等长编码，则必须满足

r≤s^l （4.10）

式中，l是等长码的码长；s是码符号集中的码元数。

例4.1中，信源X共有r=4个信源符号，二元等长编码的码符号数为s=2。根据式（4.10）可知，信源X存在唯一可译等长码的条件是码长l≥2。

如果对X的N次扩展信源X^N：{α_i=a_i1a_i2…a_iN|i=1，2，…，r^N；i₁，i₂，…，i_N=1，2，…，r}进行等长编码，由于X^N共有r^N个符号，则必须满足

r^N≤s^l （4.11）

式（4.11）表明，只有当l长的码符号序列个数（s^l）大于或等于N次扩展信源的符号个数（r^N）时，才可能存在等长非奇异码。由式（4.11）可得

当N=1，则有

可见，式（4.13）与式（4.10）是一致的。式（4.12）中，l/N是平均每个信源符号所需要的码符号个数。所以，式（4.12）表示对于等长唯一可译码，每个信源符号至少需要用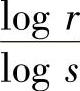个码符号来变换。也就是，每个信源符号所需最短码长为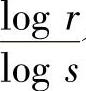个。

当s=2（二元码）时，logs=1，则式（4.12）成为

式（4.14）结果表明，对于二元等长唯一可译码，每个信源符号至少需要用logr个二元符号来编码；即对信源进行二元等长不失真编码时，每个信源符号所需码长的极限值为logr个。(www.xing528.com)

【例4.7】

英文电报有32个符号（26个英文字母加上6个字符），即r=32。若s=2，N=1（即对英文电报信源的逐个符号进行二元编码），由式（4.13）得

这就是说，每个英文电报符号至少要用5位二元符号编码才行。

由第2章已知，实际英文电报符号信源，在考虑了符号出现的概率及符号之间的依赖性后，平均每个英文电报符号所提供的信息量约为1.4bit，远小于5bit。而由第3章可知对于无噪无损二元信道，每5个二元码符号最大能载荷5bit的信息量。因此，例4.7的英文电报等长编码的信息传输速率就极低。

那么，是否可以使每个信源符号所需的码符号个数减少，也就是说是否可以提高传输效率呢？回答是可以的。这一点与式（4.12）或式（4.14）并不矛盾。因为在前面讨论的等长码中没有考虑信源符号出现的概率，以及信源符号之间的依赖关系。也就是没有考虑信源的冗余度。当考虑了信源符号的概率关系后，在等长编码中每个信源符号平均所需的码长就可以减少。

现举以下一特例，来阐明为什么每个信源符号平均所需的码符号个数可以减少。

【例4.8】设信源

而其依赖关系为P（a₂|a₁）=P（a₁|a₂）=P（a₄|a₃）=P（a₃|a₄）=1，其余P（a_j|a_i）=0。若不考虑符号之间依赖关系，此信源r=4，进行等长二元编码，由式（4.13）知l=2。

对于此特殊信源的二次扩展信源X²，因为P（a_ia_j）=P（a_i）P（a_j|a_i），由上述依赖关系可知，除P（a₁a₂）、P（a₂a₁）、P（a₃a₄）、P（a₄a₃）不等于零外，其余a_ia_j出现的概率皆为零。因此，二次扩展信源X²由4²=16个符号缩减到只有4个符号组成：

此时，对二次扩展信源X²进行等长编码，所需码长仍为l′=2。但平均每个信源符号所需码符号为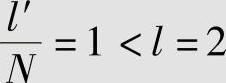。由此可见，考虑信源符号之间依赖关系后，有些信源符号序列不会出现，这样信源符号序列个数会减少，再进行编码时，所需平均码长就可以缩短。

下面仍以英文电报为例，在考虑了英文字母之间的依赖关系后，每个英文电报所需的二元码符号可以少于5。因为英文字母之间有很强的关联性，当用字母组合成不同的英文字母序列时，并不是所有的字母组合都是有意义的单词，若再把单词组合成更长的字母序列时，也不是任意的单词组合都是有意义的句子。因此，考虑了这种关联性后，在N为足够大的英文字母序列中，就有许多是无用和无意义的序列，也就是说，这些信源序列出现的概率等于零或任意小。那么，当对长为N的英文字母序列进行编码时，对于无用的字母组合、无意义的句子不编码。也就是相当于在N次扩展信源中去掉一些字母序列（这些字母序列出现的概率等于零或任意小），使扩展信源中的符号总数小于r^N，这样使编码所需的码字个数大大减少，因此平均每个信源符号所需的码符号个数就可以大大减少，从而使传输效率提高。当然，这就会引入一定的误差。但是，当N足够大后，这种误差概率可以任意小，即可以做到几乎无失真地编码。