如何判定唯一可译变长码？

给定码字集合W：{w₁，w₂，…，w_r}，对应码长为l₁，l₂，…，l_r。由定理4.3和定理4.4可知，若码长l₁，l₂，…，l_r不满足Kraft不等式的码，则一定不是唯一可译码。但码长满足Kraft不等式的码，则不一定是唯一可译码。因此，不能用Kraft不等式来判断码W是否是唯一可译码，只能根据唯一可译码的定义来判断。

根据唯一可译码的定义可知，当且仅当有限长的码符号序列能译成两种不同的码字序列，则此码一定不是唯一可译变长码。即如图4.7中情况发生，其中A_i和B_i都是码字（A_i，B_i∈W）。由图4.7可知，当图中的情况发生时，B₁一定是A₁的前缀，而A₁被B₁截去前面部分后的尾随后缀一定是另一码字B₂的前缀；B₂的尾随后缀又是其他码字的前缀。最后，码符号序列的尾部一定是某个码字。

图4.7 有限长码符号序列译成两种不同的码字序列

由此可得，唯一可译码的判断方法是：

将码W中所有码字可能的尾随后缀组成一个集合F，当且仅当集合F中没有包含任一码字，则可以判断此码W为唯一可译变长码。

可以按如下步骤构成集合F：

首先，观察码W中最短的码字是否是其他码字的前缀。若是，将其所有可能的尾随后缀排列出。而这些尾随后缀又可能是某些码字的前缀，再将由这些尾随后缀产生的新的尾随后缀列出。然后再观察这些新的尾随后缀是否是某些码字的前缀，再将产生的尾随后缀列出。依次下去，直至没有一个尾随后缀是码字的前缀或没有新的尾随后缀产生为止。

这样就获得由最短的码字能引起的所有尾随后缀。接着，按照上述步骤由短到长依次将所有码字可能产生的尾随后缀全部列出。由此得到由码W的所有可能的尾随后缀集合F。

【例4.5】

设码W：{0，10，1100，1110，1011，1101}，判断码W是否是唯一可译码。(www.xing528.com)

解 码W的最短码字为0，码字0既不是其他码字的前缀，也没有尾随后缀。

观察码字10，它是码字1011的前缀，所以有尾随后缀11。而尾随后缀11又是其他3个码字1100，1110，1101的前缀部分，由此再列出所产生的新的尾随后缀为00，10，01。它们又是一些码字的前缀部分或者某些码字是它们的前缀部分。如码字0是00和01的前缀，而10是码字1011的前缀。又得新的尾随后缀为0，11，1。然后再列出它们的尾随后缀。因为11的尾随后缀已列出，所以只需列出1的尾随后缀，直至最后全部列完为止。其中出现重复时可以略去。

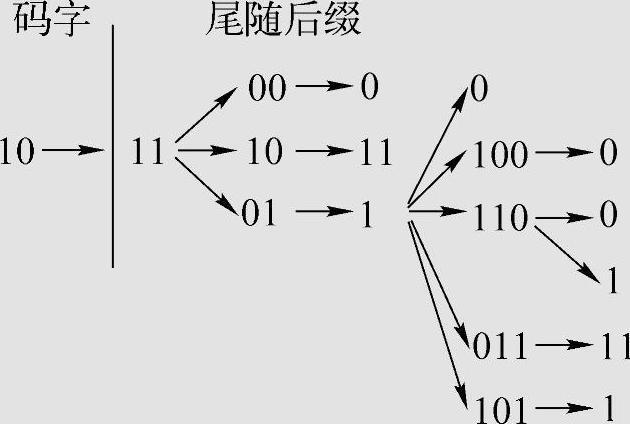
所以得尾随后缀集合F={11，00，10，01，0，1，100，110，011，101}。可见，F集中10和0都是码字，故码W不是唯一可译码。

【例4.6】

设码W：{110，11，100，00，10}，判断码W是否是唯一可译码。

解 计算码W的尾随后缀如下：

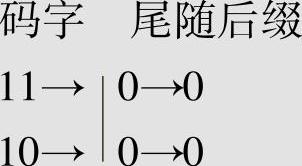
故得尾随后缀集合F={0}，F集中没有元素是码W的码字，所以码W是唯一可译码。

当然，根据这种测试方法，即时码的尾随后缀集F是空集，所以即时码一定是唯一可译码。下面分别讨论等长码和变长码的最佳编码问题，也就是是否存在一种唯一可译编码方法，使平均每个信源符号所需的码符号最短。也就是寻找无失真信源压缩的极限值。