Kraft不等式探析

由于非唯一可译码在译码时会出现歧义，因此变长码中主要研究唯一可译码，唯一可译中又以即时码为重点。关于信源符号数和码长之间满足什么关系才能构成唯一可译码和即时码，有下述定理：

定理4.2（Kraft定理）设信源符号数为r，码符号数为s，相应码字长度为l₁，l₂，…，l_r，则即时码（非延长码）存在的充要条件是：

该式称为Kraft（克拉夫特）不等式。

证明 先证明充分性，即满足不等式（4.8），一定可以构造出一种即时码。

假设满足Kraft不等式的码长为l₁，l₂，…，l_r。这r个码字中长度为i的码字共有r_i个，并设最大码长为l，则有

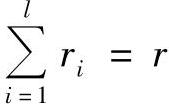
因为l₁，l₂，…，l_r满足Kraft不等式，故有

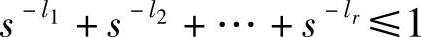
上式中，s^-1有r₁项，s^-2有r₂项，…，s^-l有r_l项，合并同类项后，变为

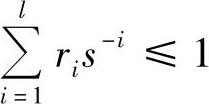
上式两端同乘s^l，得

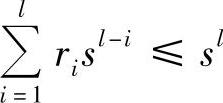
即

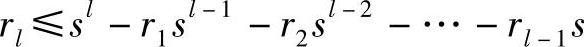
因为l、r_i、s都是正整数，所以

可以推得

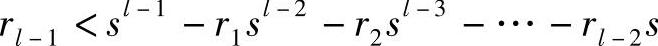
依次类推，还可以得到

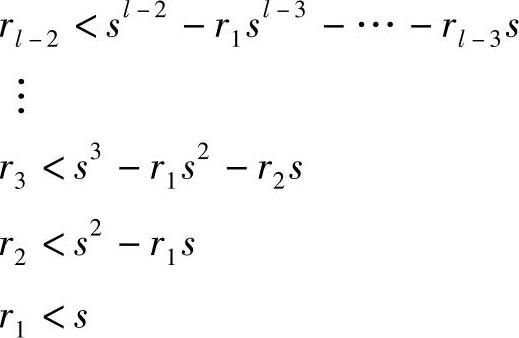
根据这些不等式，采用树图法可以构造即时码。因为码符号个数为s，故树图中一阶节点有s个，所以长度为1的可选码字最多只有s个。显然可以从这s个节点中选择r₁个节点作为终端节点，其余s-r₁个节点作为中间节点并继续延伸，引出长度为2的码字。

树图中二阶节点有（s-r₁）s=s²-r₁s个。由于r₂＜s²-r₁s，故可以从这s²-r₁s个节点中选择r₂个节点作为终端节点，其余s²-r₁s-r₂个节点作为中间节点并继续延伸，引出长度为3的码字。

树图中三阶节点有（s²-r₁s-r₂）s=s³-r₁s²-r₂s个。由于r₃＜s³-r₁s²-r₂s，故可以从这s³-r₁s²-r₂s个节点中选择r₃个节点作为终端节点，其余s³-r₁s²-r₂s-r₃个节点作为中间节点再继续延伸，引出长度为4的码字。

按此方法进行下去，当上述不等式均成立时，总可能找出r_i个节点作为终端节点，直到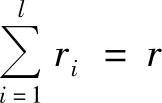，便可以构造出整个树图。

由上述码树构造过程看出，如果只取终端节点作为码字，则所得结果必为即时码。

再证明必要性，即给定码长分布为l₁，l₂，…，l_r的即时码后，其码长一定满足不等式（4.8）。只需要将上述证明过程反推回去即可。

【证毕】

Kraft不等式是1949年由克拉夫特（L.G.Kraft）提出，并在即时码条件下给予证明。Kraft不等式给出了即时码的码长必须满足的条件。1956年麦克米伦（B.McMillan）证明，对于唯一可译码也满足此不等式。这说明唯一可译码的码长选择上并不比即时码有更宽松的条件。

定理4.3 设信源符号数为r，码符号数为s，相应码字长度为l₁，l₂，…，l_r，则唯一可译码存在的充要条件是满足Kraft不等式，即。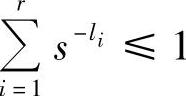

证明 先证充分性。由于即时码一定是唯一可译码，所以由定理4.2可知，充分性成立。再证必要性。对任意n，有等式

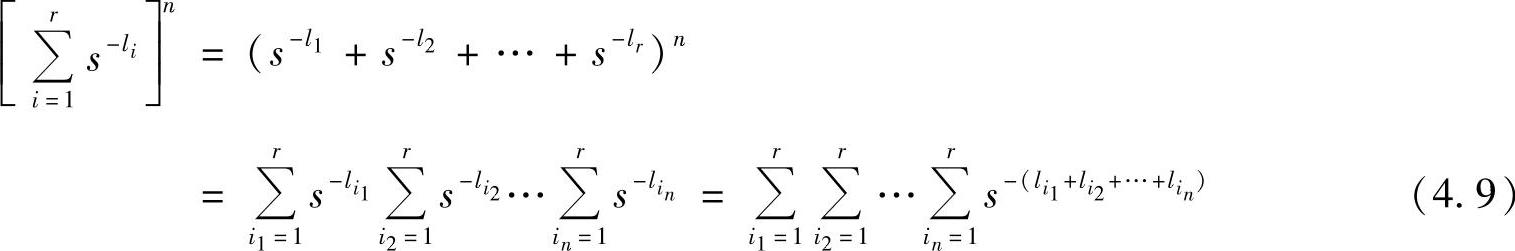
该式最右边共有rⁿ项，代表了n个码字组成的码字序列的总数。令(www.xing528.com)

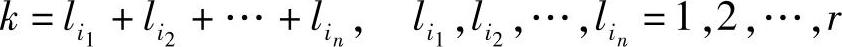
即k可以视为由n个长度分别为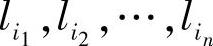的码字组成的码字序列的总长度。

因为是变长码，假设单个码字的码长的取值范围是l_min≤l_i≤l_max，且l_min≥1，故有

nl_min≤k≤nl_max

在rⁿ个码字序列中，码符号序列总长度为k的码字序列的个数为n_k，于是，式（4.9）的右边经合并同类项后，有

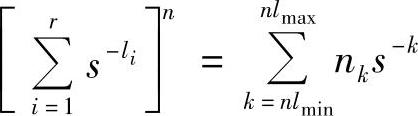
因为已知是唯一可译码，故总长为k的所有码字序列必定是不相同的，即非奇异的，故必存在下列关系：

于是有

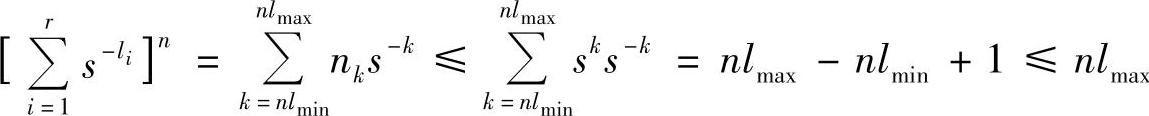
因此，有

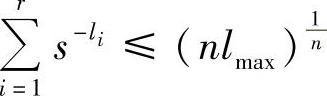
因为对于一切正整数n，上式均成立，所以可以取极限

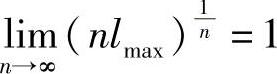
故

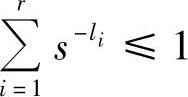
【证毕】

由定理4.2和定理4.3可以得到一个重要结论（定理4.4），即任何唯一可译码均可以用一个即时码来代替，而不改变任一码字的长度。因此要构造唯一可译码，只需讨论构造即时码就可以了。

定理4.4 若存在一个码长为l₁，l₂，…，l_r的唯一可译码，则一定存在具有相同码长的即时码。

证明 根据定理4.3，由唯一可译码可以推出满足Kraft不等式，再根据定理4.2，可以推出存在码长为l₁，l₂，…，l_r的即时码。

【证毕】

【例4.4】（续例4.1）

分析表4.1给出的7种编码方法的码长是否能构成即时码（或唯一可译码）。

解 码W₁、码W₂：

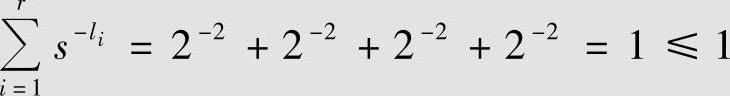
因此，必存在至少一种码长为2、2、2、2的二元即时码（或唯一可译码）。码W₁就是一个例子，它既是唯一可译码，又是即时码。

码W₃、码W₄：

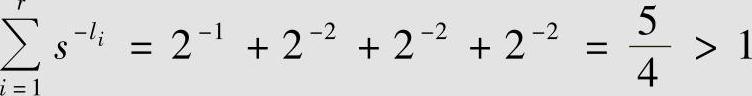
因此，码长为1、2、2、2的二元码必不可能是即时码（或唯一可译码）。

码W₅、码W₆、码W₇：

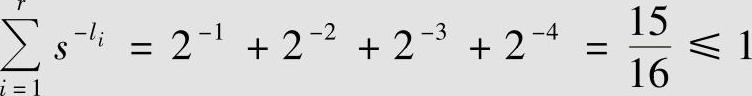
因此，必存在至少一种码长为1、2、3、4的二元即时码（或唯一可译码）。码W₆和码W₇既是唯一可译码，又是即时码。码W₅是唯一可译码，但不是即时码。