信源编码树图表达

一个信源编码的全部码字可以方便地表示在一个树图上，且即时码的树图结构与非即时码的树图结构有重要差别，因此，利用树图法来分析和构造即时码是一种有效的方法。

给定码字集合W：{w₁，w₂，…，w_r}，可以用码树来描述。树（树图）是由一个根（树根）、若干树枝（枝）和若干节点组成。例如，表4.1中码W₆可以用图4.3所示的码树来表述；图4.4给出了二元码和三元码的树图结构。

码树图中的最上端A点为根，从根出发向下伸出树枝，树枝的数目一般等于码符号的总数s。例如，二元编码时s=2，就伸出两条树枝；三元编码时s=3，就伸出3条树枝。

树枝的尽头为节点，从节点出发再伸出树枝，每次每个节点伸出至多s条树枝，依次下去构成一棵树（不过它是倒长的）。

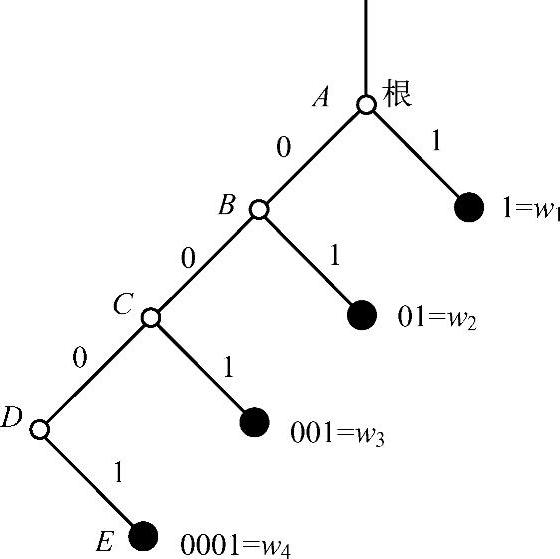
图4.3 表4.1中码W₆的码树

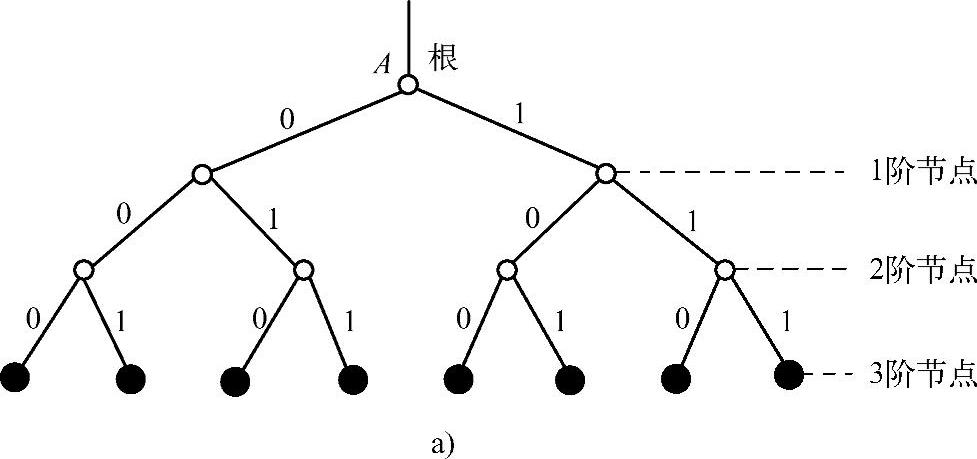
图4.4 码树图

a）二元码树

当某一节点被安排为码字后，它就不再继续伸树枝，此节点称为终端节点（用粗黑点表示）。而其他节点称为中间节点，中间节点不安排为码字（用空心圈表示）。给每个节点所伸出的树枝分别从左向右标上码符号0，1，…，s-1。这样，终端节点所对应的码字就由从根出发到终端节点走过的路径所对应的码符号组成。图4.3中，码字w₄对应于终端节点E，其走过的路径ABCDE所对应的码符号分别为0、0、0、1，则码字w₄为0001。

可以看出，按树图法构成的码一定满足即时码的定义。因为从根到每一个终端节点所走的路径是不同的，而且中间节点不安排为码字，所以一定满足对前缀的限制。

另外，从码树上可以得知，当第i阶的节点作为终端节点，且分配以码字，则码字的码长为i。(www.xing528.com)

任一即时码都可以用树图法来表示。但当码字长度给定，即时码不是唯一的。图4.3中，将0、1码符号从右向左标号，即得即时码W={0，10，110，1110}，如图4.5所示。

用树图法也可以画出表4.1中码W₅所对应的码树，如图4.6所示。由图可见，该码树从根到终端节点所经路径上每一个中间节点皆为码字，因此不满足前缀条件。虽然码W₅不是即时码，但它是唯一可译码。

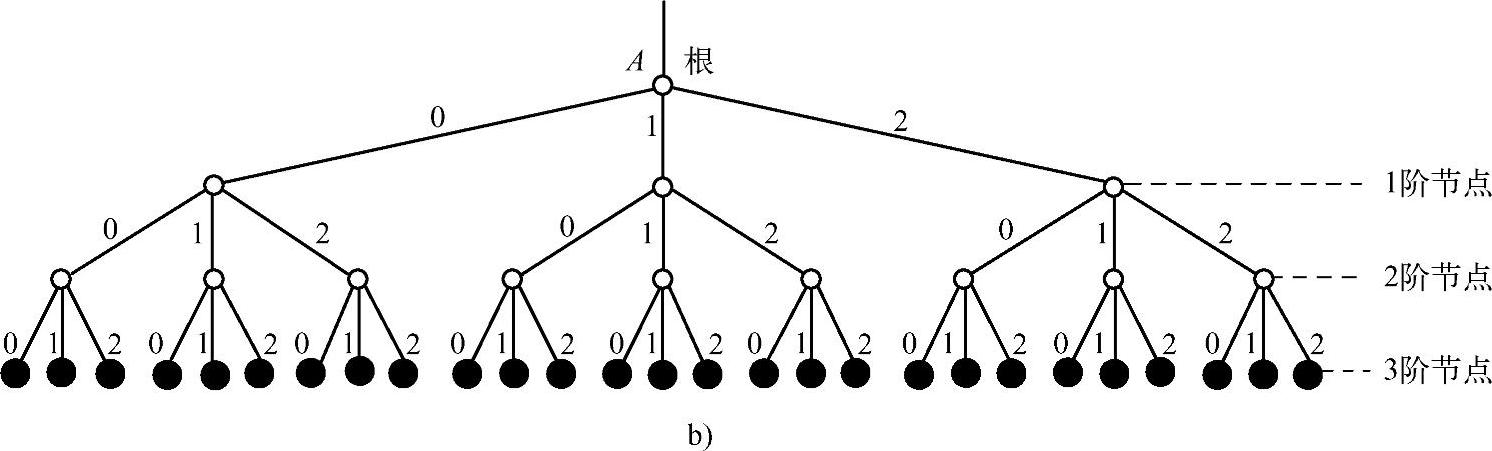
图4.4 码树图（续）

b）三元码树

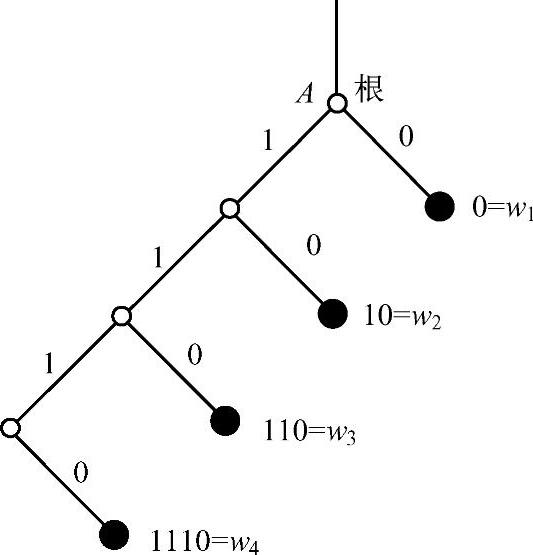
图4.5 表4.1中码W₆的另一种码树

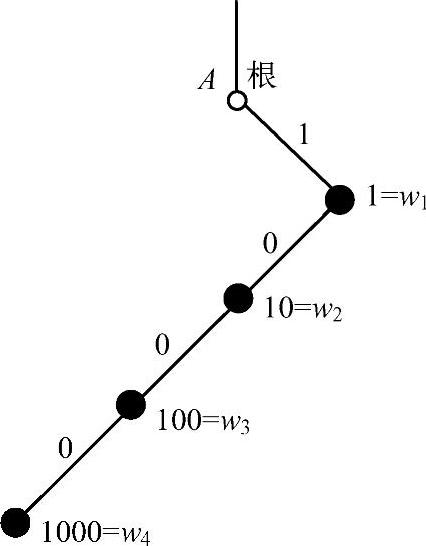
图4.6 表4.1中码W₅的码树

在每个节点上都有s个分枝的树称为整树，如图4.4所示；否则称为非整树，如图4.3和图4.5所示。当s元l节的码树的所有树枝都被用上时，第l阶节点共有s^l个终端节点，正好对应于长度为l的等长码，可见等长码也是即时码的一种。

即时码的码树图还可以用来译码。当接收到一串码符号序列后，首先从树根出发，根据接收到的第一个码符号来选择应走的第一条路径。若沿着所选支路走到中间节点，那就再根据接收到的第二个码符号来选择应走的第二条路径。若又走到中间节点，那就再依次继续下去，直到终端节点为止。走到终端节点，就可以根据所走的路径，立即判断出所接收的码字。同时使系统重新返回树根，再作下一个接收码字的判断。这样就可以将接收到的一串码符号序列译成对应的信源符号序列。