平均码长和编码效率优化方法

用码符号Y对信源X进行编码，可以设计出多种即时码或唯一可译码。从高效率传输或存储信息的观点来考虑，希望选择由短的码符号组成的码字，就是用码长作为选择准则，为此引入码的平均长度的概念。

设信源为

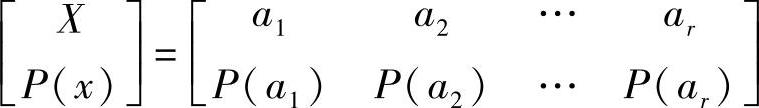
对每个信源符号a₁，a₂，…，a_r编码，编码后的码字为w₁，w₂，…，w_r，各码字对应的码长分别为l₁，l₂，…，l_r。因为对于唯一可译码来说，信源符号与码字一一对应，所以有

P（w_i）=P（a_i），i=1，2，…，r

定义4.9 信源编码的平均长度（平均码长）为

L是每个信源符号平均需用的码元数。

当信源给定时，信源的熵H（X）（bit/信源符号）就确定了，而编码后每个信源符号平均用L码元来变换。为此引入信息传输率的概念。

定义4.10 平均每个码元携带的信息量，即编码后信道的信息传输率（又称编码速率、码率）为

若传输一个码符号平均需要t秒，则编码后每秒传输的信息量为

可见，L越短，R或R_t越大，信息传输的能力就越强。因此，无失真信源编码的基本问题就是找使平均码长最小的编码。为此，给出最佳码的定义。

定义4.11 对于某一信源和某一码符号集来说，若有一个唯一可译码，其平均码长小于所有其他唯一可译码的平均码长，则该码称为最佳码（或紧致码）。

假设码元为s进制的，即可能取s种可能值，则每个码元所能载荷的最大信息量为R_max=log s bit/码元，因此，为衡量信源编码的效能，引入编码效率的概念。(www.xing528.com)

定义4.12 信源编码的编码效率为每个码元载荷的平均信息量与其所能载荷的最大信息量的比值，表示为

【例4.3】（续例4.1）

计算表4.1中即时码W₁、W₆和W₇的平均码长、码率和编码效率。

解 表4.1中采用的是二元编码，s=2，每码元符号携带的最大信息量为R_max=log s=1 bit/码元。信源X的熵为

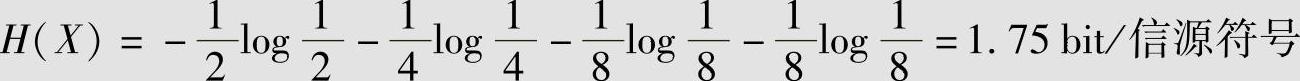
码W₁是等长编码，其平均码长为L_W1=2码元/信源符号，码率为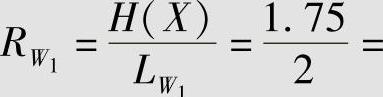0.875 bit/码元，编码效率为。

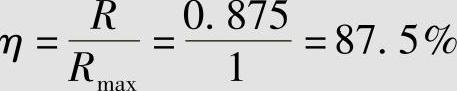码W₆和W₇是变长编码，尽管这两种编码的码字集相同，但由于信源符号与码字的对应关系不同，编码的效能是不同的。码W₆和W₇的平均码长分别为

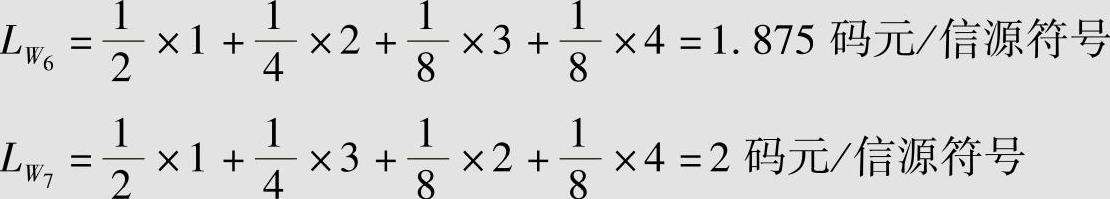
码W₆和W₇的码率分别为

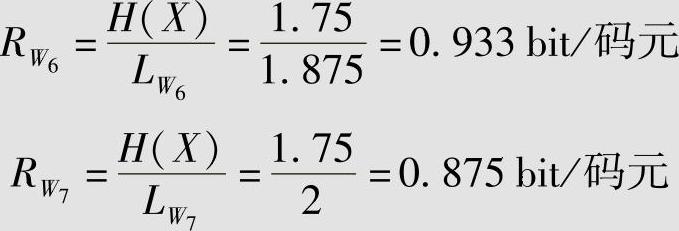
码W₆和W₇的编码效率分别为

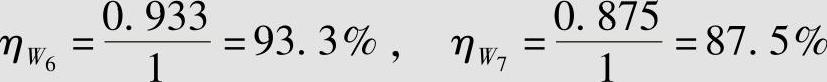
由例4.3的结果可以看出，采用变长编码可以提高编码效率，如变长码W₆的编码效率为93.3%，比等长码W₁的编码效率87.5%高出很多。但是，如果码字符号集相同，与信源符号的对应关系改变后会影响编码的性能，如变长码W₇的码字符号集尽管与变长码W₆相同，但编码效率相差很多。