信源编码基本码型解析

下面给出一些常用码及其定义。

定义4.1（二元码和多元码） 若码符号集元素个数为2，所编出的码称为二元码（或二进制码）；否则称为多元码（或多进制码）。

若将信源通过一个二元信道进行传输，为了使信源适合信道传输，就必须把信源符号变换成0、1符号组成的码符号序列（二元序列），这种编码所得的码为二元码，例4.1（表4.1）中的编码即为二元码。二元码是数字通信和计算机系统中最常用的一种码。

定义4.2（等长码和变长码） 若码中所有码字的码长都相同，则称为等长码；若码中所有码字的码长不都相同，则称为变长码。

表4.1中，码W₁和码W₂是等长码；码W₃～码W₇是变长码。

定义4.3（非奇异码和奇异码） 若码中所有码字都不相同，则称此码为非奇异码；若码中有相同的码字，则称此码为奇异码。

表4.1中，码W₁是等长非奇异码；码W₄～码W₇是变长非奇异码。对于码W₂，由于a₁和a₄都编码为序列00，因此是等长奇异码；对于码W₃，由于a₂和a₄都编码为序列11，因此是变长奇异码。由于奇异码不能保证译码时的唯一性，因此，实际的无失真信源编码一定是非奇异码。以下仅讨论非奇异码。

定义4.4（同价码） 若码符号集中每个码符号所占的传输时间都相同，则所得的码为同价码。

一般二元码是同价码。本章讨论的都是同价码。对同价码来说，等长码中每个码字的传输时间都相同；而变长码中每个码字的传输时间就不一定相同。电报中常用的莫尔斯码是非同价码，其码符号划（-）是码符号点（·）传输时间的三倍。

定义4.5（码的M次扩展码） 假定某码W，它把信源X中的符号a_i一一变换成码W中的码字w_i，则码W的M次扩展码是所有M个码字组成的码字序列的集合。

根据定义，若码W：{w₁，w₂，…，w_r}（或W：{w₁，w₂，…，w_rN}），则码W的M次扩展码为

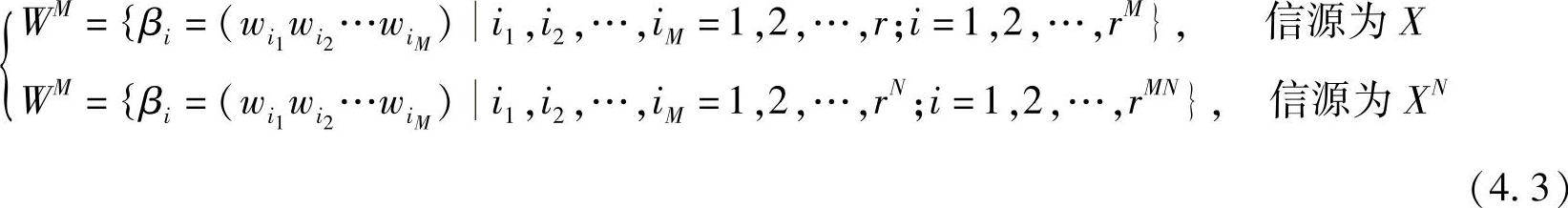
可见，码W的M次扩展码W^M中，每个码字β_i与M次扩展信源X^M（或（X^N）M）中每个信源符号序列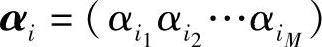一一对应。但是要注意，码W的M次扩展码W^M与N次扩展信源符号集X^N的编码是不同的。

【例4.2】（续例4.1）

对信源X的编码方案W₆，构造其二次扩展码。因为信源X的二次扩展信源为

X²={α₁=a₁a₁，α₂=a₁a₂，α₃=a₁a₃，…，α₁₆=a₄a₄}

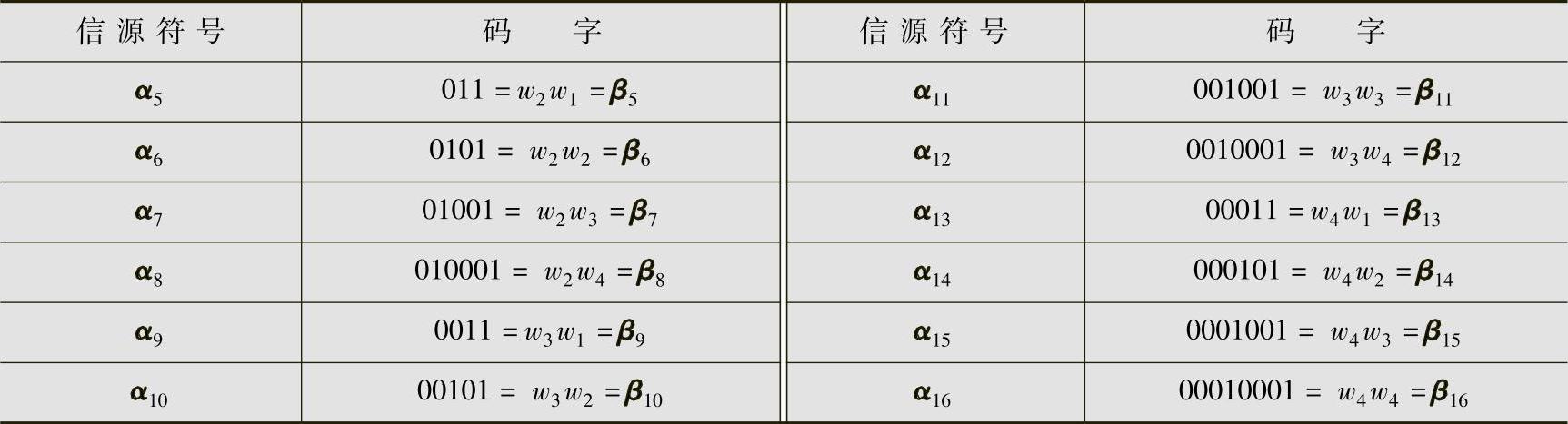
所以，码W₂的二次扩展码见表4.2。

表4.2 信源X的编码W₂的二次扩展码（例4.2）

（续）

定义4.6（唯一可译码） 若码的任意一串有限长的码符号序列只能被唯一地译成所对应的信源符号序列，则此码称为唯一可译码（或单义可译码）；否则，就称为非唯一可译码（或非单义可译码）。(www.xing528.com)

若要求所编的码是唯一可译码，不但要求编码时不同的信源符号变换成不同的码字（即使用非奇异码），而且还必须要求任意有限长的信源序列所对应的码符号序列各不相同，即要求码的任意有限长M次扩展码都是非奇异码。因为只有这样，才能把该码符号序列唯一地分割成一个个对应的信源符号，从而实现唯一的译码。所以，某码的任意有限长M次扩展码都是非奇异码，则该码为唯一可译码。

表4.1中的等长编码中，码W₁是唯一可译码；码W₂因其奇异性，是非唯一可译码。

表4.1中的变长编码中，同样因为奇异性，码W₃是非唯一可译码；而码W₄的有限长的码符号序列能译成不同的信源符号序列，如码符号序列为0100时可译成a₁a₂a₁或a₄a₃，因此，W₄是非唯一可译码。可以验证，码W₅～码W₇是唯一可译码。

码W₅～码W₇虽然都是唯一可译码，但它们还有不同之处。比较码W₅与码W₆或码W₇，会发现在码W₆和码W₇中，每个码字都以符号1为结束码元。这样，在接收码符号序列过程中，只要一出现1时，就知道一个码字已经终结，新的码字就要开始。所以当出现符号1后，就可以立即将接收到的码符号序列译成对应的信源符号。可见码字中的符号1起到逗点的作用，故称为逗点码。

而码W₅情况就不同，对于这类码，当收到一个或几个码符号后，不能即时判断码字是否已经终结，必须等待下一个或几个码符号收到后才能作出判断。例如，当已经收到两个码符号10时，不能判断码字是否终结，必须等下一个码符号到达后才能决定。如果下一个码符号是1，则表示前面已经收到的码符号10为一码字，把它译成信源符号a₂；如果下一个符号仍是0，则表示前面收到的码符号10并不代表一个码字，这时真正的码字可能是100，也可能是1000，到底是什么码字还需等待下一个符号到达后才能作出决定，因此码W₅不能即时进行译码。

定义4.7（即时码）在唯一可译变长码中，若译码时无须参考后续的码符号就能立即作出判断，译成对应的信源符号，则这类码称为即时码。

逗点码（如表4.1中码W₆和码W₇）就是一种即时码。

再来分析表4.1中的码W₅和码W₆的结构会发现，这两类码之间有一个重要的结构上的不同点。在码W₅中，码字w₂=10是码字w₃=100的前缀，而码字w₃=100又是码字w₄=1000的前缀，或者说码字w₂=10是码字w₁=1的延长（加一个0），而码字w₃=100又是码字w₂=10的延长（再加一个0）。但是在码W₆中找不到任何一个码字是另外一个码字的前缀。当然也就没有一个码字是其他码字的延长。因此，给出如下定义：

定义4.8（非延长码）若码W中，没有任何完整的码字是其他码字的前缀，即设w_i=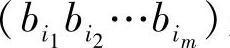是码W中的任一码字，而它不是其他码字

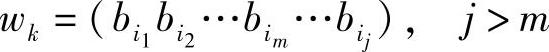
的前缀，则此码称为非延长码（或前缀条件码）。

定理4.1 一个唯一可译码为即时码的充要条件是该码为非延长码。

证明 充分性是显然的。因为如果没有一个码字是其他码的前缀，则在接收到一个相当于一个完整码字的码符号序列后，便可以立即译码，而无须考虑其后的码符号。

必要性用反证法证明。假设一个相反情况，设码w_i是w_j的前缀，则当收到相当于w_i的码符号序列后，还不能即刻作出判断。因为它可能是码字w_i，也可能是码字w_j的前缀部分，还必须参考以后一些符号的到达，才能作出正确判断，这与即时码的定义相矛盾。从而证明了必要性。

【证毕】

即时码（非延长码）是唯一可译码的一类子码，所以即时码一定是唯一可译码，反之唯一可译码不一定是即时码。因为存些非即时码（延长码），它具有唯一可译性，但不满足前缀条件（如表4.1中码W₅）。可以用图来描述这些码之间的关系，如图4.2所示。

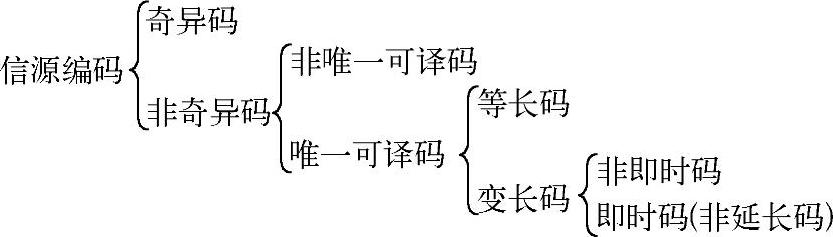
图4.2 码的分类

本节讨论对信源进行变长编码的问题。变长码往往在信源扩展次数N不很大时就可以编出效率很高而且无失真的码。

同样，变长码也必须是唯一可译码，才能实现无失真编码。对于变长码，要满足唯一可译性，不但码本身必须是非奇异的，而且其任意有限长M次扩展码也都必须是非奇异的。所以，唯一可译变长码的任意有限长M次扩展码都是非奇异码。