并联信道及其信道容量分析与优化

并联信道存在不同的类型，如图3.23所示。其中图3.23a称为输入并接信道，可以看成一个单输入多输出的信道，或者可以认为将相同的消息通过多个子信道发送给收信方；图3.23b称为并用信道，它将N个符号通过N个子信道独立地发送给收信方；图3.23c称为和信道，它每一次只单独地使用其中的一个子信道传输消息。

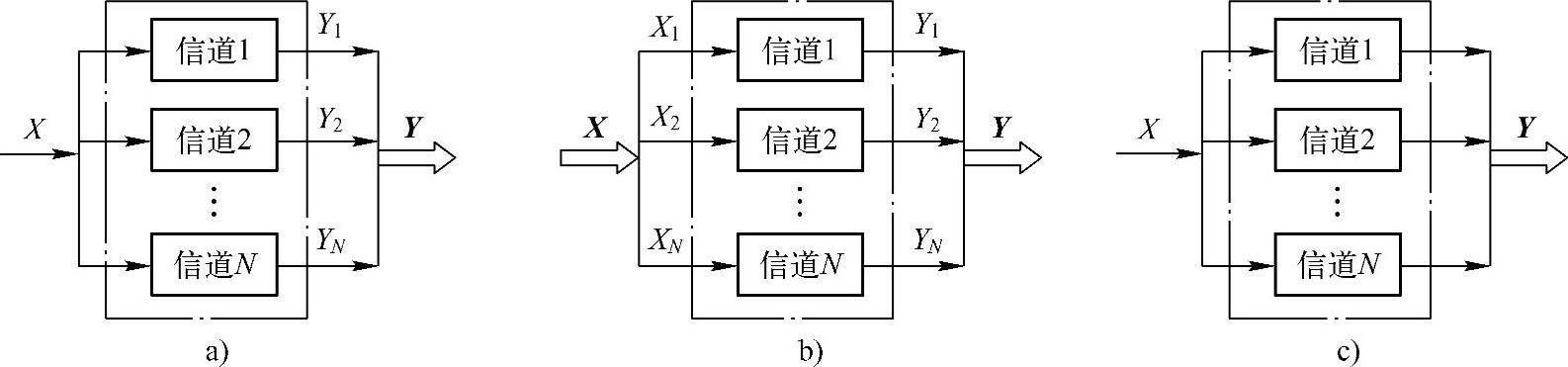
图3.23 并联信道的分类

a）输入并接信道 b）并用信道 c）和信道

1.输入并接信道

输入并接信道的输入为随机变量X，X被送入N个子信道同时进行传输；输出为随机序列Y=（Y₁，Y₂，…，Y_N）。输入并接信道的输入随机变量X和输出随机序列Y之间满足

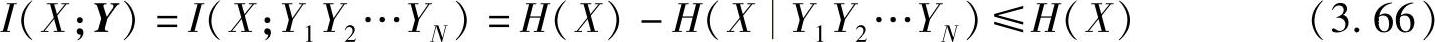
根据信道容量的定义，输入并接信道的容量为

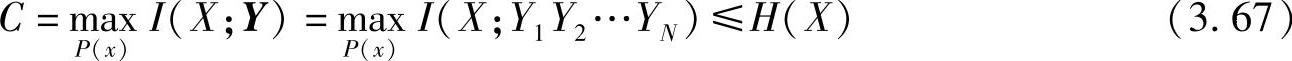
利用平均互信息的性质（性质2.36）：I（X；YZ）=I（X；Z）+I（X；YZ），可以推导出输入并接信道的平均互信息关系式为

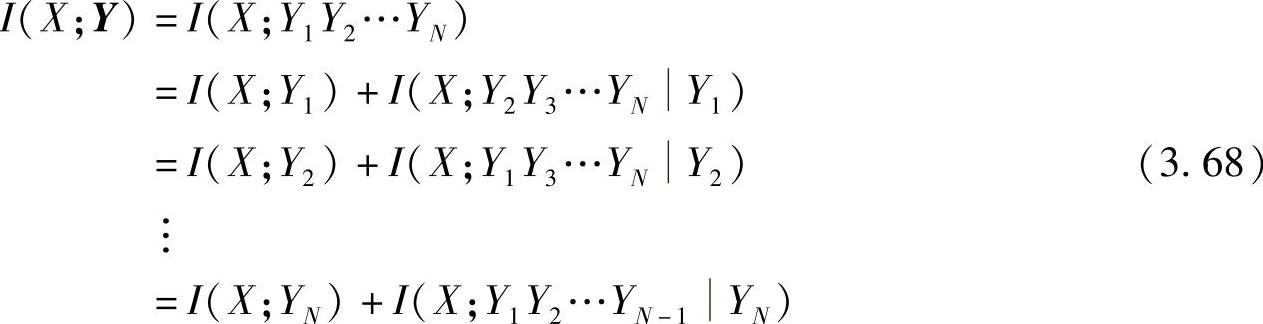
因为互信息是非负的，由式（3.68）和式（3.67）可以看出，输入并接信道容量C大于等于任意的子信道的信道容量，但是小于等于信源的极大熵log r（r是输入符号的个数）。

2.并用信道(www.xing528.com)

并用信道又称为独立并联信道，也等价于时变的N次无记忆扩展信道，即联合信道的转移概率是无记忆的。并用信道的输入为随机序列X=（X₁，X₂，…，X_N），输出为随机序列Y=（Y₁，Y₂，…，Y_N），信道模型如图3.23b所示，其中N个信道之间是独立并联关系。因此，由离散序列信道的定理3.5知，该信道的平均互信息满足

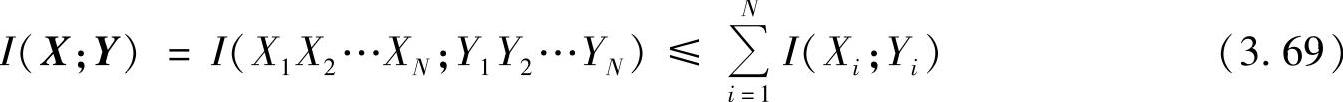
当且仅当输入X_i（i=1，2，…，N）相互独立时，式（3.69）等号成立。所以，并用信道容量为

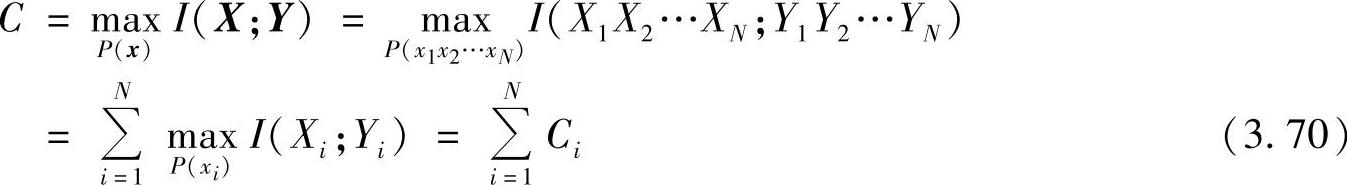
式中，C_i是子信道i的信道容量。

可见，并用信道容量为被并联的信道容量之和，且每一信道的输入达到各自信道对应的最佳概率分布时，平均互信息量才能达到信道容量。

注：在一些文献和教材上表述的并用信道容量存在差异。有些结论为“并用信道容量不大于被并用的信道容量之和，只有当输入X_i（i=1，2，…，N）相互独立时取等号”。但考虑到信道容量是一个与信源特性无关的信道特征参数的特点，本书采用式（3.70）的结论。

3.和信道

在N个并联信道中，以概率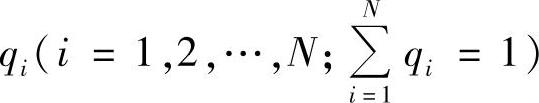选择子信道i来单独地传输信源消息，这种并联信道就是和信道。和信道容量的计算较为复杂，下面仅给出结果。详细证明请参考文献[19]和[20]。

定理3.8 对于由N个子信道组成的和信道，其信道容量为

式中，C_i是子信道i的信道容量。第i个子信道的使用概率为q_i=2^Ci-C（i=1，2，…，N），达到信道容量的输入概率为各子信道达到容量时的概率乘以q_i。