串联信道的信道容量和数据处理定理

在一些实际通信系统中常常出现串联信道的情况。如微波中继接力通信就是一种串联信道。又如在无线电数字通信（如卫星通信）中，发信端将数字以0、1二元码的形式进行编码后以脉冲波形的形式发送；收信端实际收到的是一系列幅度不同的波形信号，需要经过判决器后输出相应的发送符号的估计值。此时，将发信端到收信端看成是一个离散信道，其输入符号为0、1二元码，输出符号为一系列不同幅度的数值。对于门限判决器，也可以将它看成是另一个信道，其输入符号为一系列不同幅度的数值（即前一信道的输出），输出为0、1二元码。因此，从无线电数字通信系统的发信端到门限判决器的输出端可以看成是两个信道的串联。本小节将研究串联信道的互信息问题。

串联信道又称为级联信道，其信道模型如图3.20a所示。假设信道Ⅰ和信道Ⅱ都是离散单符号信道。其中，信道Ⅰ的输入随机变量为X，其值域为A：{a₁，a₂，…，a_r}；信道Ⅰ的输出随机变量，也是信道Ⅱ的输入随机变量为Y，其值域为B：{b₁，b₂，…，b_s}；信道Ⅱ的输出随机变量为Z，其值域为C：{c₁，c₂，…，c_t}。信道Ⅰ的转移概率为P（y|x）=P（b_j|a_i）（i=1，2，…，r；j=1，2，…，s），而信道Ⅱ的转移概率一般与前面两个随机变量X和Y都有关，所以记为P（z|xy）=P（c_k|a_ib_j）（i=1，2，…，r；j=1，2，…，s；k=1，2，…，t）。

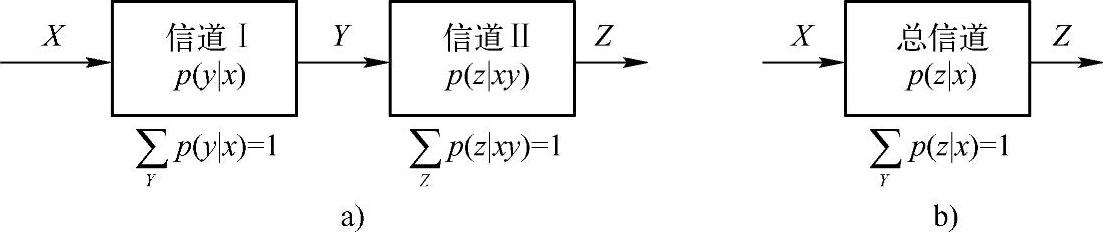
图3.20 串联信道和等价信道

a）串联信道 b）等价信道

若信道Ⅱ的转移概率使其输出Z仅与输入Y有关，与前面的输入X无关，即满足

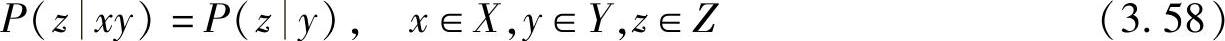
则称这两个信道的输入和输出X、Y、Z序列构成马尔可夫链。

这两个信道的串联可以等价成一个总信道（如图3.20b所示），其信道转移概率为

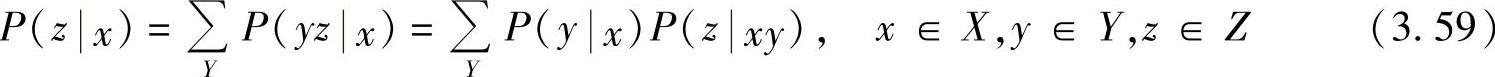
若随机变量X、Y、Z满足马尔可夫链，即满足式（3.58），则式（3.59）可以进一步表示为

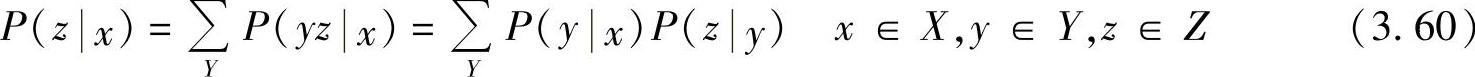
式（3.60）可以改写成总信道转移概率矩阵的形式，其表达式为

对于串联信道中的平均互信息，有以下两个重要定理：

定理3.6 串联信道的平均互信息满足

当且仅当对所有的x、y、z，满足P（z|xy）=P（z|y）时，式（3.62）等号成立；满足P（z|xy）=P（z|x）时，式（3.63）等号成立。

证明 根据平均互信息的定义，有

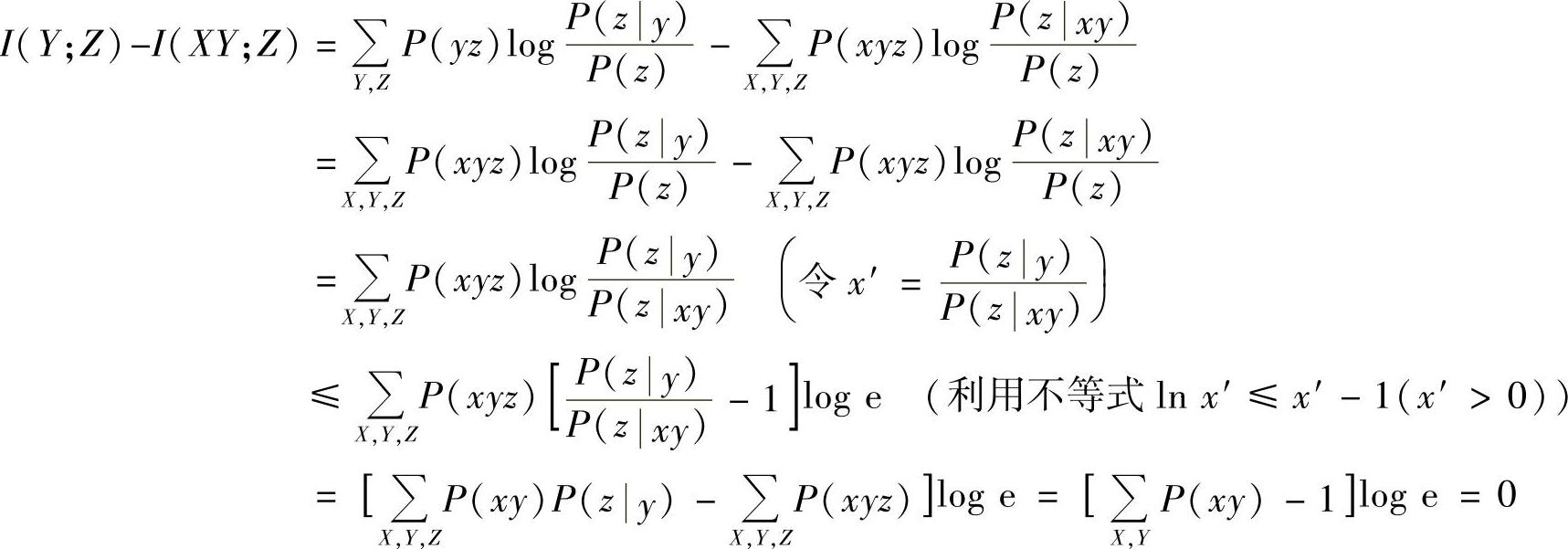
故证得I（Y；Z）≤I（XY；Z），即式（3.62）成立。又因为x′=1是ln x′≤x′-1（x′＞0）的等号成立的充要条件，因此，式（3.62）等号成立的充要条件是，即P（z|xy）=P（z|y）。同理，可证式（3.63）成立。

【证毕】

定理3.7（数据处理定理）若随机变量X、Y、Z构成一个马尔可夫链，则有

证明 因为随机变量X、Y、Z组成马尔可夫链，故有P（z|xy）=P（z|y），于是由平均互信息的定义式可以直接得到I（XY；Z）=I（Y；Z）。将该结果代入式（3.63），即可以证明式（3.65）成立。其中，等式成立的条件是P（z|xy）=P（z|x）。

因为X、Y、Z是马尔可夫链，可以证明Z、Y、X也是马尔可夫链，所以有P（x|zy）=P（x|y），运用与证明式（3.65）相同的证明方法，并注意到平均互信息的互易性，可以证明式（3.64）成立。

【证毕】(www.xing528.com)

定理3.7的重要性在于其含义，通过多个串联的信道传输的信息量，不会大于每一个信道传输的信息量。换句话说，信息量越传越少，不会增加，至多保持原来的信息量不变。这同时也说明了，信道只是信息传输的通道，不是信息的源泉，信息归根到底来源于信源。因此，定理3.7也称为数据处理定理。

数据处理定理说明，在任何信息传输系统中，最后获得的信息至多是信源所提供的信息。如果一旦在某一过程中丢失一些信息，以后的系统不管如何处理，都不能再恢复已经丢失的信息。这就是信息不增性原理。这一点深刻反映了信息的物理性质。

但是在实际工程上，总是要对数据进行处理的，因为只有这样才能保留住对信宿有用的信息，去掉无用的信息或干扰。例如，为了看清楚图像，要尽量去除杂波；为了听到悦耳的声音，要尽量滤除掉噪声。虽然信息的总量减少了，但对信宿的有用信息突出了，最终使得信宿的总体体验增强了。

【例3.13】

串联信道如图3.21a所示，X、Y、Z构成马尔可夫链，求总的信道转移概率矩阵。

解 由图3.21a可知，信道Ⅰ和信道Ⅱ的信道转移概率矩阵分别为

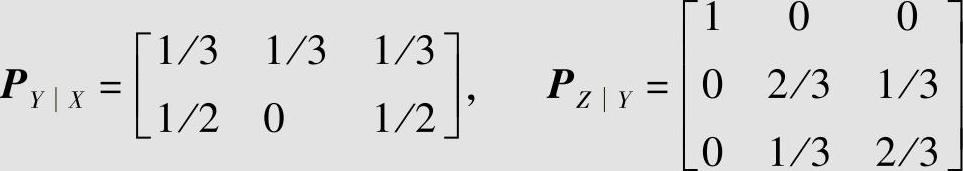
由于X、Y、Z构成马尔可夫链，由式（3.61）可得总信道转移概率矩阵为

因此，串联信道的等价信道为图3.21b所示的信道。

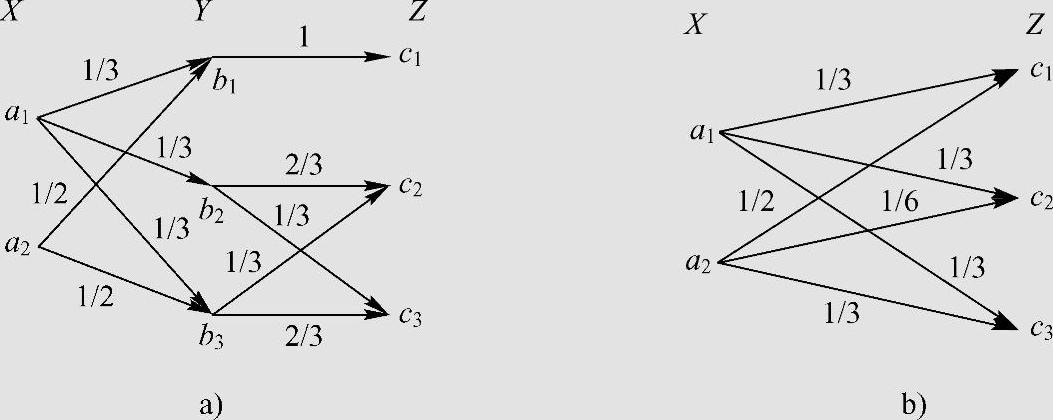
图3.21 例3.13的串联信道和等价信道

a）串联信道 b）等价信道

【例3.14】

求N个相同的二元无记忆对称信道组成的串联信道的信道容量。

解 设单个二元无记忆对称信道的转移概率矩阵为

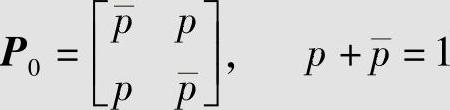
其中，p是信道的错误转移概率。于是N个二元无记忆对称信道串联后的信道转移概率矩阵为P=P^N₀。设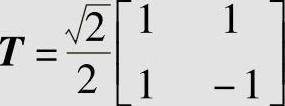，可以验证T=T^-1，且有Λ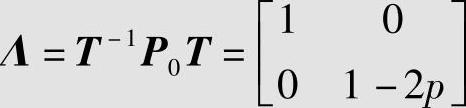，所以

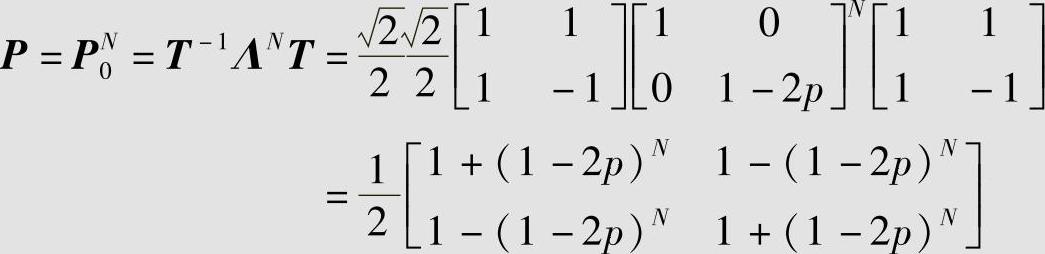
可见，N个二元无记忆对称信道串联后的总信道还是二元无记忆对称信道，其信道容量为

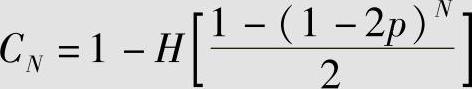
当串联级数趋向无穷时，有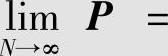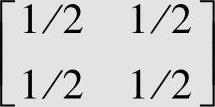，此时，串联信道的容量为0。

图3.22是不同串联级数时串联信道容量与单一信道错误转移概率p的关系曲线。可见，随着串联级数的增加，信道容量在减少。当信道错误转移概率p很小（例如p=10^-4）时，信道容量的减小量较小。所以，串联级数N较大时，串联信道容量虽减小，但仍有一定的数值。而实际数字通信系统中，二元对称信道的p值一般在10^-6～10^-4以下。所以，若干次串联后信道容量的减少并不明显。

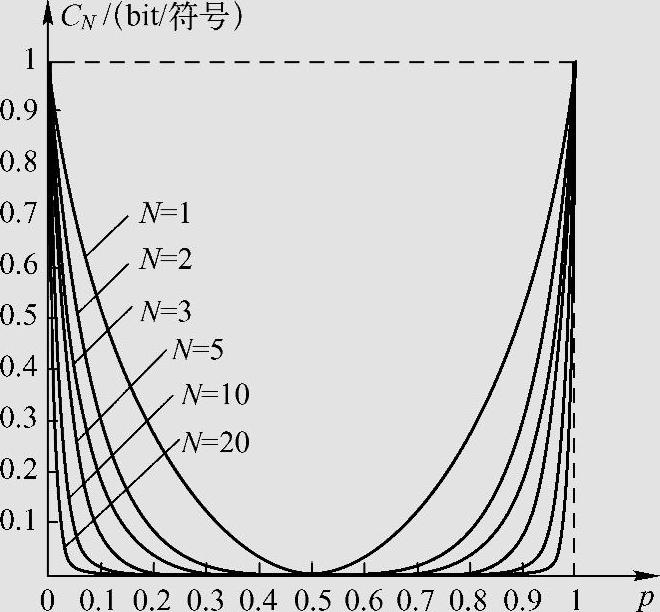
图3.22 N级二元对称信道串联的信道容量