离散序列信道的信道容量分析

根据平均互信息的定义，可得N次扩展信道的平均互信息为

在一般离散信道中，信道输入和输出两个离散随机序列之间的平均互信息I（X；Y），与两个序列中对应的离散随机变量之间的平均互信息I（X_i；Y_i）（i=1，2，…，N）存在以下关系。

定理3.5 离散序列信道[X，P（y|x），Y]的平均互信息I（X；Y）有下列性质：

1）当信道是无记忆的，即信道转移概率满足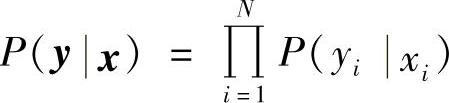时，有

2）当信道的输入信源是无记忆的，即信源概率满足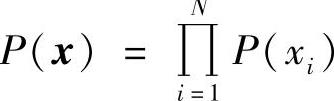时，有

3）当信道和信源都是无记忆的，有

证明1）由平均互信息的定义式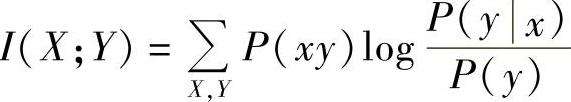，计算下式：

所以，当信道是无记忆的，即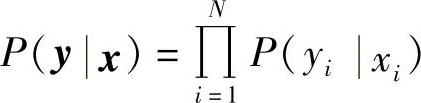时，有

证得式（3.50）成立。

2）由平均互信息的定义式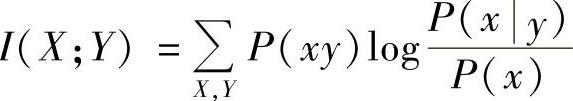，用与证明1）中的类似方法，计算下式：

所以，当信源是无记忆的，即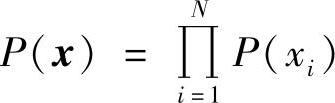时，有

证得式（3.51）成立。

3）由定理中的1）和2），显然可得到式（3.52）成立。

【证毕】(www.xing528.com)

若信道的输入序列X=（X₁，X₂，…，X_N）中的随机分量X_i（i=1，2，…，N）不但取自于同一信源符号集，并且具有同一种概率分布，而且通过相同的信道传输到收信端（即信道转移概率分布不随i而改变，为时不变信道），因此

I（X₁；Y₁）=I（X₂；Y₂）=…=I（X_N；Y_N）=I（X；Y）

得

所以，对于离散无记忆信道的N次扩展信道，有

I（X；Y）≤NI（X；Y） （3.54）

若输入信源也是无记忆的，有

I（X；Y）=NI（X；Y） （3.55）

式（3.55）说明，当信源是无记忆时，无记忆的N次扩展信道的平均互信息等于原来信道的平均互信息的N倍。

一般的离散无记忆信道的N次扩展信道应满足式（3.50），所以，其信道容量为

式中，C_i是i时刻通过离散无记忆信道传输的最大信息量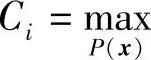，I（X_i；Y_i）。因为现有输入随机序列X=（X₁，X₂，…，X_N）在同一信道中传输（也可以认为在时不变信道中传输），所以得C_i=C（i=1，2，…，N）。即任何时刻通过离散无记忆信道传输的最大信息量相同，代入式（3.56），得

C^N=NC （3.57）

式（3.57）说明，离散无记忆N次扩展信道容量等于原单符号离散信道容量的N倍。且只有当输入信源无记忆，且分别达到最佳输入概率分布时，才能达到这个信道容量NC。

通常，消息序列在离散无记忆N次扩展信道中传输的信息量I（X；Y）≤NC。