离散序列信道的数学模型优化

现实中信道的输入和输出一般不是单个符号，往往是空间和（或）时间上离散的随机序列，信道或者可以近似认为是无记忆的，但是更多的却是明显有记忆的，即序列的转移概率之间存在相关性。在这类信道中，最为简单的是平稳无记忆信道；有记忆信道一般较为复杂，有时可以简化为平稳的、记忆有限的信道。

定义3.10 离散序列信源X=（X₁，X₂，…，X_N）的各分量X_i（i=1，2，…，N）在N个不同时刻分别通过离散单符号信道[X_i，P（y_i|x_i），Y_i]（i=1，2，…，N），在收信端收到相应的输出分量Y_i（i=1，2，…，N），并组成随机序列Y=（Y₁，Y₂，…，Y_N），这样形成的新信道称为离散序列信道[X，P（y|x），Y]。

图3.18是离散序列信道模型。由于信道相当于离散单符号信道在N个不同时刻，连续运用了N次，所以也称为离散单符号信道的N次扩展信道。

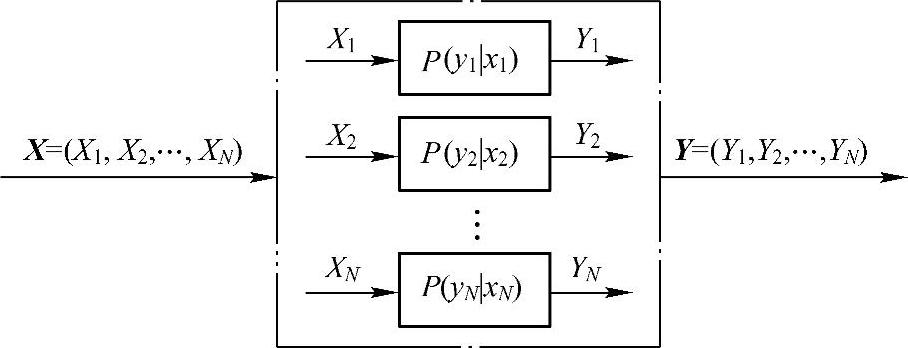
图3.18 离散单符号信道的N次扩展信道模型

信源序列X的随机分量X_i（i=1，2，…，N）的值域为输入符号集A：{a₁，a₂，…，a_r}，则N次扩展信源X共有r^N个不同的元素α_k（k=1，2，…，r^N）。

输出序列Y的随机分量Y_i（i=1，2，…，N）的值域为输出符号集B：{b₁，b₂，…，b_s}，则N次扩展输出信源Y共有s^N个不同的元素β_h（h=1，2，…，s^N）。

序列信道容量的计算较为复杂，这里仅考虑较为简单的序列信道。

对于一般的离散单符号信道，其信道容量的计算需附加许多条件，并通过复杂的迭代运算才能求得。不过一旦得到离散单符号信道容量，它的离散无记忆序列信道容量就较为容易求得。

假设信道输入序列为x=（x₁，x₂，…，x_N），输出序列为y=（y₁，y₂，…，y_N），由于无记忆，可得相应转移概率为。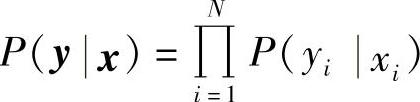

设离散单符号信道[X，P（y|x），Y]的信道转移概率矩阵为

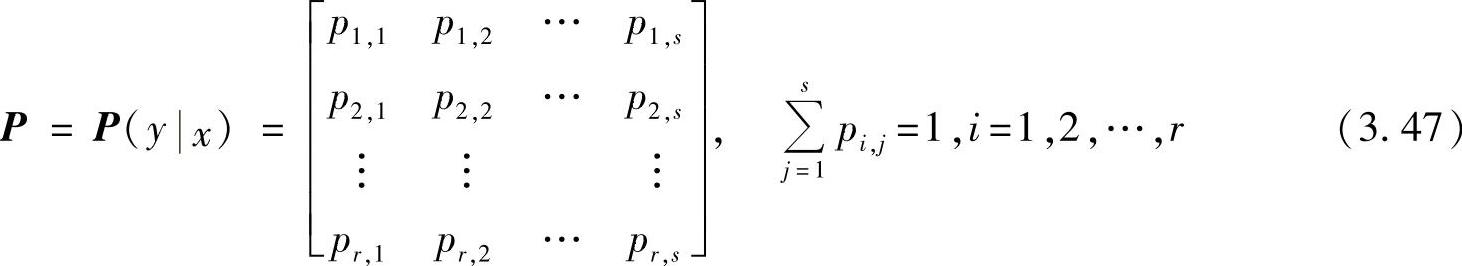
则此离散无记忆序列信道[X，P（y|x），Y]的数学模型可以用图3.18表示。

设离散无记忆序列信道的输入序列X产生的事件x为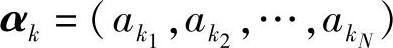，共有r^N个，其中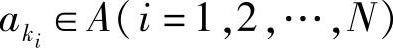；输出序列Y产生的事件y为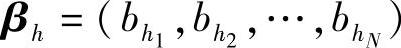，共有s^N个，其中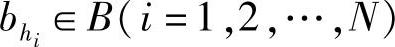。因此，其序列信道转移概率矩阵为

(www.xing528.com)

式中，。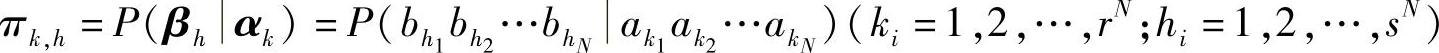

由无记忆性，可得下列关系式：

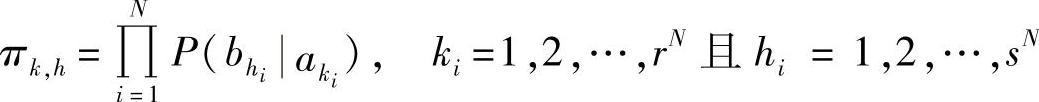
【例3.12】

求图3.5中二元无记忆对称信道的二次扩展信道。

二元对称信道的输入和输出随机变量X和Y的值域都是A，B：{0，1}。因此，二次扩展信道的输入符号集为A²：{00，01，10，11}，共有2²=4个符号；输出符号集为B²：{00，01，10，11}，也共有4个符号。根据无记忆信道的特性，求得二次扩展信道的转移概率为

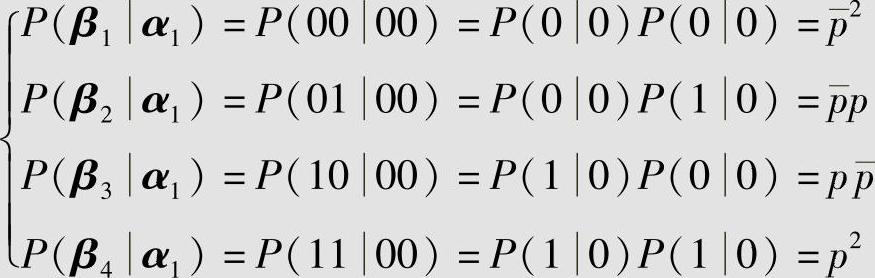
同理，可以求得其他转移概率π_k，h，最后得二次

扩展信道的信道转移概率矩阵π，即

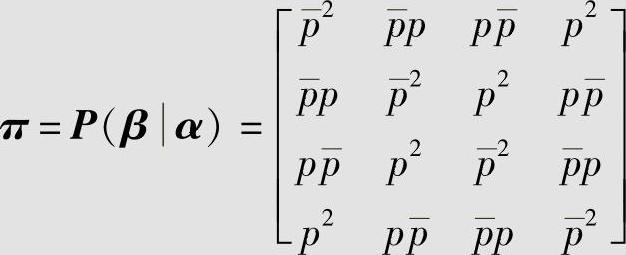
上述二次扩展信道可以用图3.19表示。

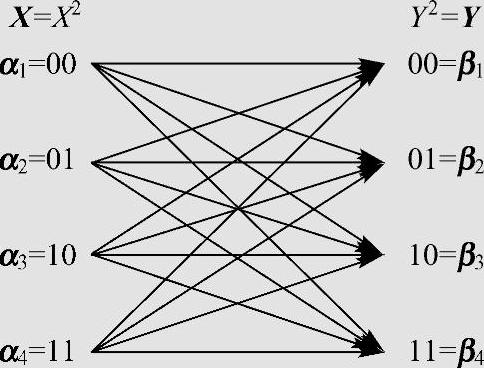
图3.19 二元对称信道的二次扩展信道模型