一般离散信道的信道容量优化方案

根据定义式（3.17），信道容量就是在固定信道条件下，对所有可能输入概率分布P（x）求平均互信息的极大值。由性质2.34知，I（X；Y）是输入概率分布P（x）的∩形凸函数，所以极大值一定存在。而I（X；Y）是r个变量P（a_i）（i=1，2，…，r）的多元函数，并满足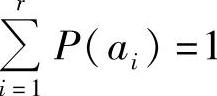。所以，可以运用拉格朗日乘子法来计算这个条件极值，其求解步骤如下：

1）引进一个新函数

式中，λ是拉格朗日乘子（待定常数）。

2）求Φ的偏导数并置为零，然后解方程组

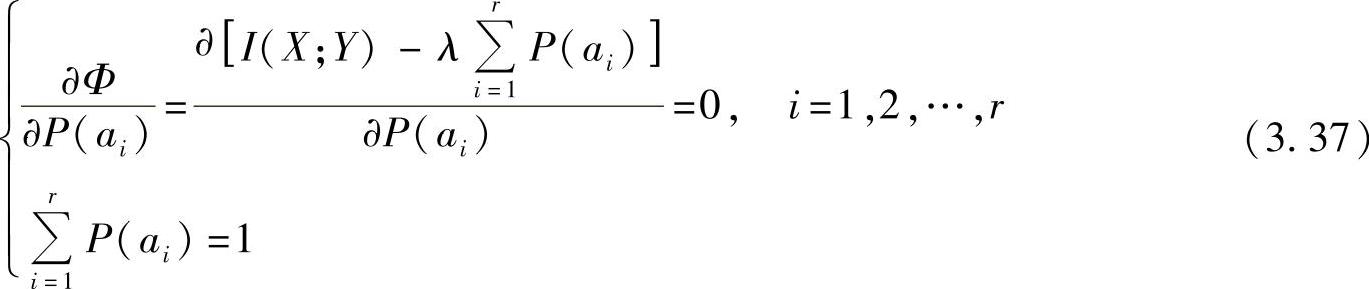
可以先求解出达到极值的概率分布P（a_i）（i=1，2，…，r）和拉格朗日乘子λ的值。

3）再求解出信道容量C。因为

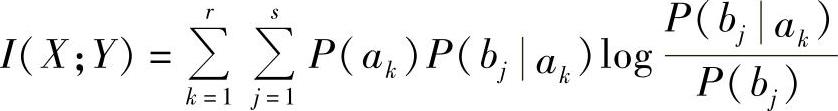
而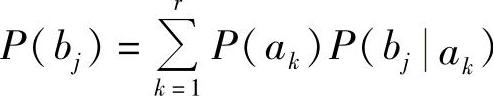，所以

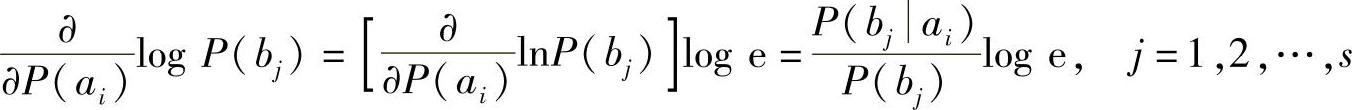
由式（3.37）中的第一个方程，得

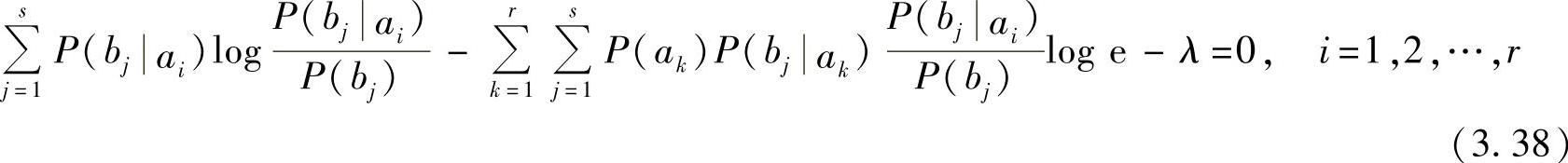
又因为

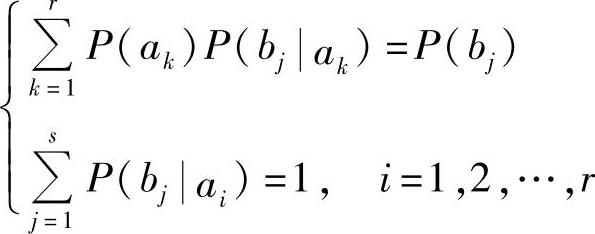
所以，方程组（3.37）变换成

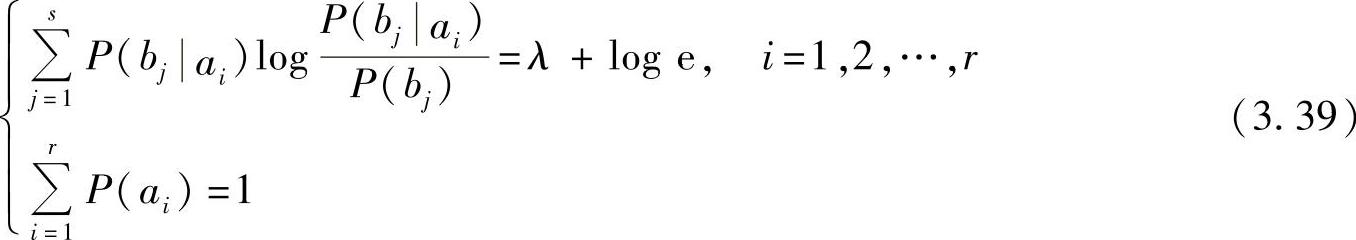
假设解得的平均互信息I（X；Y）达到极值的最佳输入概率分布是P（a_i）（i=1，2，…，r），然后把式（3.39）中的前r个方程式两边分别乘以达到极值的概率P（a_i），并求和，得

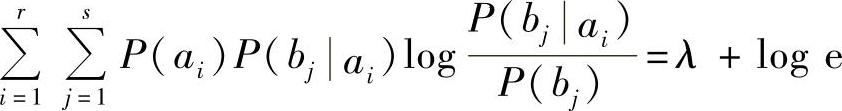
上式左边即是信道容量，所以得

C=λ+log e （3.40）

由于

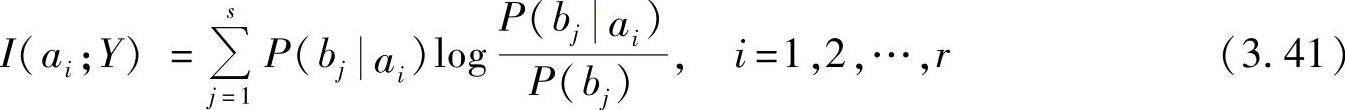
式中，I（a_i；Y）是收信端接收到Y后获得关于x=a_i的信息量，即是信源符号x=a_i对收信端Y平均提供的互信息。式（3.41）中对数取不同的底就得到相应不同的单位。

通常I（a_i；Y）值与a_i有关。但对于最佳输入概率分布，根据式（3.39）和式（3.40），得

I（a_i；Y）=C，i=1，2，…，r

所以，对于一般离散信道有下述的定理。

定理3.4 一般离散信道的平均互信息I（X；Y）达到极大值（即等于信道容量）的充要条件是输入概率分布P（a_i）（i=1，2，…，r）满足

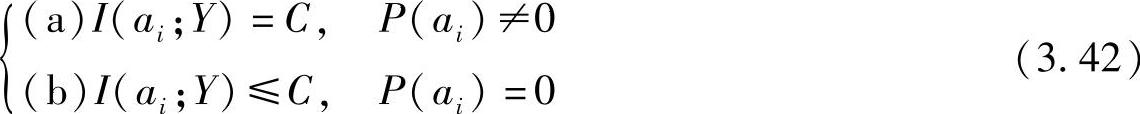
这时，C就是信道容量。

由定理3.4可以得出结论，当信道的平均互信息达到信道容量时，输入信源符号集中每一个信源符号a_i，对收信端Y提供相同的互信息，只是概率为零的符号除外。

这个结论和直观概念是一致的。在某一给定的信源分布下，若信源符号a_i对收信端所提供的平均互信息I（a_i；Y）比其他符号提供的平均互信息大。那么，就可以用提高P（a_i）的方法来增大总的平均互信息。但是，这就会改变信源的概率分布，必然使符号a_i的平均互信息I（a_i；Y）减小，而其他符号对应的平均互信息增加。所以，经过不断调整信源的概率分布，就可以使每一个概率不为零的信源符号对收信端提供相同的平均互信息。

定理3.4只给出了达到信道容量时信源概率分布应满足的充要条件，并没有给出最佳输入概率分布的值P（a_i）（i=1，2，…，r），因而，也没有给出信道容量的计算公式。另外，定理本身也隐含着，达到信道容量的最佳输入概率分布并不一定唯一，只要信源概率分布满足条件式（3.42），并使I（X；Y）最大，就都是信道的最佳输入概率分布。

定理3.4可以用于计算特殊情况下的信道容量。下面举例说明。

【例3.9】

某离散信道如图3.15所示，输入符号集为A：{a₁，a₂，a₃}，输出符号集为B：{b₁，b₂，b₃}，信道转移概率矩阵为

求信道容量及其最佳输入概率分布。

解 该信道不是离散对称信道，无法用前面给出的公式计算信道容量。

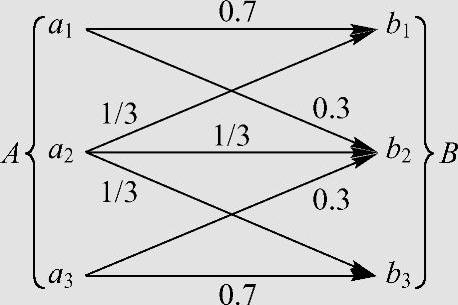
图3.15 例3.9的离散信道

考查此信道，设想若输入符号a₂的概率P（a₂）=0，该信道就成为一个二元对称删除信道。若输入符号a₂的概率P（a₂）≠0，就会增加不确定度。

于是假设输入概率分布为P（a₁）=P（a₃）=1/2，P（a₂）=0，然后检查是否满足求解信道容量的充要条件。

根据假设的输入概率分布，容易求得P（b₁）=P（b₃）=0.35，P（b₂）=0.3。

根据式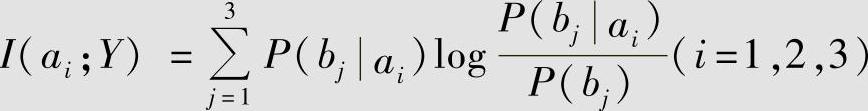，计算得(www.xing528.com)

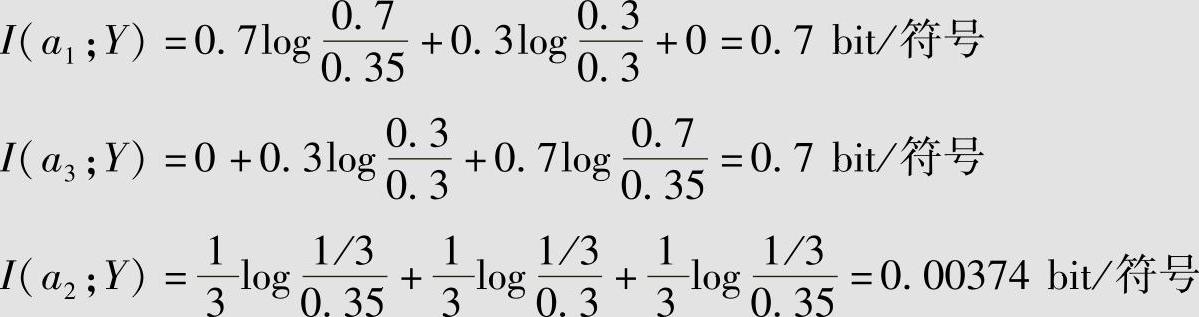
可见，此假设分布满足定理3.4的充要条件，因此，该信道容量为C=0.7 bit/符号。最佳输入概率分布是P（a₁）=1/2，P（a₂）=0，P（a₃）=1/2。

【例3.10】

某离散信道如图3.16所示，输入符号集为A：{a₁，a₂，a₃，a₄}，输出符号集为B：{b₁，b₂}，信道转移概率矩阵为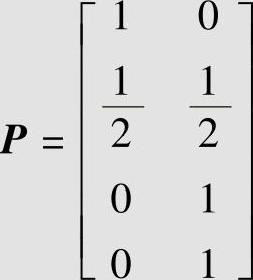，求信道容量及其最佳输入概率分布。

解 分析信道特性。由于输入符号a₂转移到b₁和b₂是等概率的，所以a₂可以略去。而且a₁与a₃、a₄都分别传输到b1与b₂，因此可以只取a₁和a₃。于是，假设最佳输入概率分布为P（a₁）=P（a₃）=1/2，P（a₂）=P（a₄）=0。

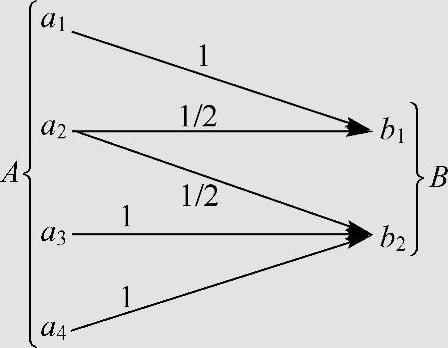
图3.16 例3.10的离散信道

根据假设的输入概率分布，容易求得P（b₁）=P（b₂）=1/2。

根据式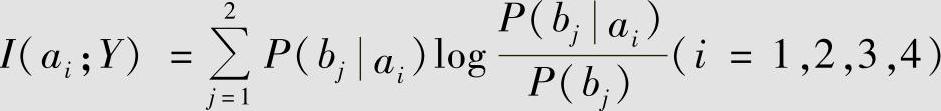，计算得

I（a_i；Y）=1 bit/符号，i=1，3，4

I（a₂；Y）=0 bit/符号

可见，此假设分布满足定理3.4的充要条件，因此，该信道容量为C=1 bit/符号。最佳输入概率分布是P（a₁）=1/2，P（a₂）=0，P（a₃）=1/2，P（a₄）=0。

若再假设最佳输入概率分布为P（a₁）=P（a₄）=1/2，P（a₂）=P（a₃）=0。同理推得，该概率分布也满足定理3.4的充要条件，且信道容量也是C=1 bit/符号。

由例3.10再一次看到，信道的最佳输入概率分布不是唯一的。互信息I（a_i；Y）仅与信道转移概率和输出概率分布有关，因而达到信道容量的输入概率分布不是唯一的，但输出概率分布是唯一的。

对于一般的离散信道很难利用定理3.4来寻求信道容量和对应的输入概率分布。因此，仍只能采用求解方程组式（3.39）的方法。

根据式（3.40），把式（3.39）中前r个方程改写成

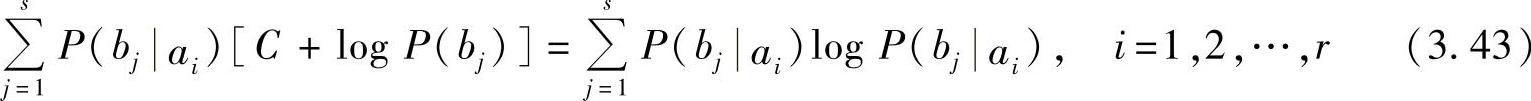
令β_j=C+logP（b_j）（i=1，2，…，r），代入式（3.43），得

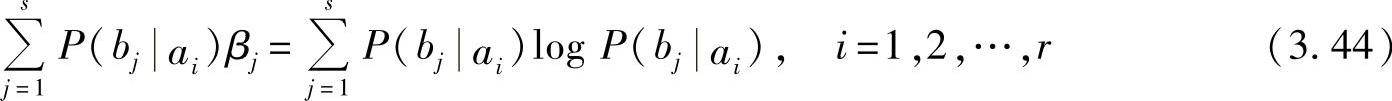
这是含有s个未知数，有r个方程的非齐次线性方程组。

如果设r=s，且信道转移概率矩阵P是非奇异矩阵，则此方程组有解，并且可以求出βj的数值，然后根据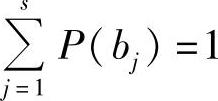的附加条件求得信道容量为

由C值就可以解出对应的输出概率分布为

再根据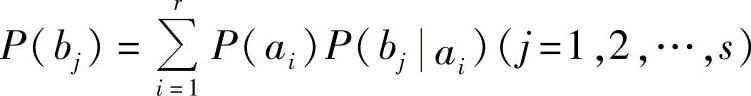，即可以解出达到信道容量的最佳输入概率分布P（a_i）（i=1，2，…，r）。

【例3.11】

某离散信道如图3.17所示，输入符号集为A：{a₁，a₂，a₃，a₄}，输出符号集为B：{b₁，b₂，b₃，b₄}，信道转移概率矩阵为，求信道容量及其最佳输入概率分布。

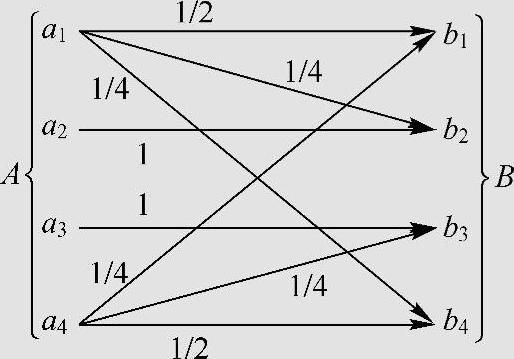
图3.17 例3.11的离散信道

解 该信道是非对称信道，且无法利用定理3.4来计算信道容量。但信道转移概率矩阵为方阵，且为非奇异矩阵。所以，根据式（3.44）得

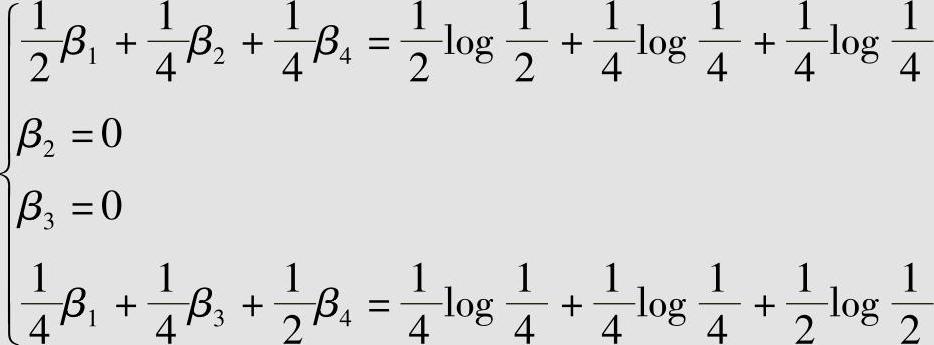
取对数2为底解方程组，得β₂=β₃=0，β₁=β₄=-2。由式（3.45），得信道容量

C=log（2^-2+2⁰+2⁰+2^-2）=log 5-1 bit/符号

又根据式（3.46），得

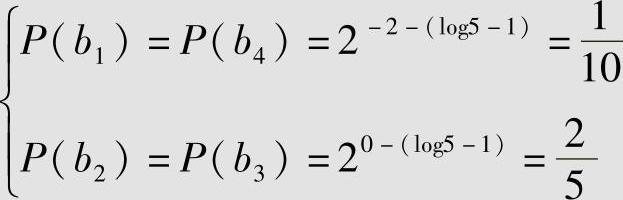
因此，解得最佳输入分布为

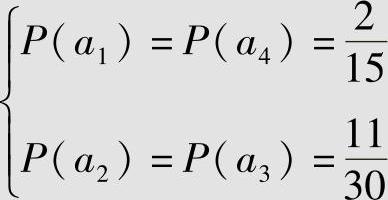
上述求得P（a_i）（i=1，2，3，4）都大于零，故求得的结果是正确的。

有时所求得的P（a_i）（i=1，2，…，r）并不一定满足概率的条件，这是由于采用拉格朗日乘子法时并没有加入P（a_i）≥0（i=1，2，…，r）的条件，所以必须对解进行检查。如果解得所有的P（a_i）≥0（i=1，2，…，r），则上述的解就是正确的解；如果有某些P（a_i）=0，则需要重新进行计算；如果有某些P（a_i）＜0，则上述解无效，此时，表明所求得的值出现的区域不满足概率条件，极大值必在边界上。于是，必须假设某些输入符号的概率为零，然后重新进行计算。

若r＜s，求解非齐次线性方程组就比较困难，即使已求出解，也无法保证都满足P（a_i）≥0（i=1，2，…，r）。因此，必须反复进行试运算，这时运算变得十分复杂，常采用计算机迭代算法求解离散无记忆信道容量。具体迭代算法可以参考有关文献[15]。

关于信道容量的注释如下：

1）达到信道容量时的最佳输入概率分布不一定是唯一的。但对称信道和准对称信道的最佳输入概率分布是唯一的，且为等概率分布。

2）达到信道容量时，输出概率严格为正。

3）对应于信道容量的输出概率分布是唯一的。