离散准对称信道的信道容量优化

定义3.9 如果信道转移概率矩阵P是输入对称的，不是输出对称的，则称该信道是离散准对称信道。

准对称信道是对称信道的推广，对称信道是准对称信道的特例。例3.4中的两个信道是准对称信道。

由于转移概率矩阵每行元素相同，所以式（3.27）～式（3.29）成立。这样准对称信道的容量也是求某种信源的概率分布，使H（Y）取极大值的问题。由于准对称信道不是输出对称的，不存在信源X的某一分布使得输出Y是等概率分布，而具有极大熵log s。在输入对称的条件下，H（Y）的极大值可能小于Y等概率的熵。因此，准对称信道的容量满足

C≤log s-H（p′₁，p₂′，…，p_s′） （3.33）

求解准对称信道的容量较为复杂。但因准对称信道转移概率矩阵的行具有对称性，而列不满足对称性。这样的信道可以以矩阵的列为单位分解为若干个行和列都是对称的子矩阵的形式，其信道容量就可以利用这种分解后的矩阵表达来计算。下面两个定理给出了有关准对称信道的容量的结果，定理的完整证明请参考文献[5]和[13]。

定理3.2 当且仅当信源是等概率分布时，离散准对称信道达到信道容量值，且信道容量为

C=H（Y）-H（p′₁，p₂′，…，p_s′）（3.34）

定理3.3 离散准对称信道容量的表达式为

式中，r是信源的符号个数；p′₁，p₂′，…，p_s′是信道转移概率矩阵的行元素；N_k是第k个子矩阵中行元素之和；M_k是第k个子矩阵中列元素之和；n是不相交的子矩阵的个数。

显然，由于对称信道是准对称信道的特例，定理3.2和定理3.3同样适用于对称信道容量的计算。(www.xing528.com)

【例3.8】

已知离散准对称信道的转移概率矩阵，求信道容量。

解 信源符号为a₁、a₂，3个输出符号为b₁、b₂、b₃；设P（a₁）=α，P（a₂）=1-α。

计算方法一：由P（b_j）=P（a₁）P（b_j|a₁）+P（a₂）P（b_j|a₂），得

令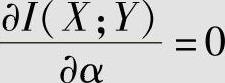，可以解得α=1/2，代入上式计算得信道容量为

C=I（X；Y）|_α=1/2=0.0365 bit/符号

计算方法二：根据定理3.2计算。当P（a₁）=P（a₂）=1/2时，计算得P（b₁）=P（b₂）=0.4，P（b₃）=0.2。由式（3.34），该离散准对称信道容量为

计算方法三：根据定理3.3计算。该离散准对称信道转移概率矩阵可以分解为两个互不相交的对称的子矩阵

由式（3.35）计算该离散准对称信道容量为