探究信道疑义度、噪声熵和信息传输率

信源X以某种随机方式产生消息x，消息x经过信道传输后在收信端得到对应的输出消息y，所有的输出消息y组成信宿Y。研究信道就是在固定信道的情况下（即已知信道转移概率P（y|x）），研究信息在信道上的传输问题。

平均互信息I（X；Y）是用来定量分析集合X和Y之间信息交互的数学工具。2.4节的分析指出，信道输入符号集X和输出符号集Y之间平均互信息I（X；Y）就是该信道上传输的信息量，或者说是经过通信后收信端接收到的信息量。

平均互信息的关系式I（X；Y）=H（X）-H（X|Y）=H（Y）-H（Y|X）表明，收信端收到的信息量与条件熵H（X|Y）和H（Y|X）有密切关系。为此，给出如下定义：

定义3.1 称信道输出Y条件下，信道输入X的条件熵

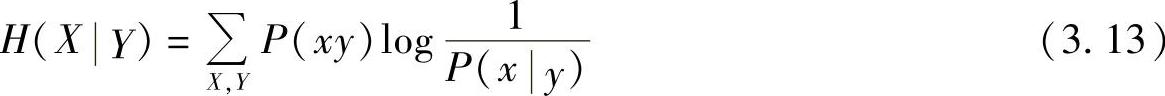
为信道疑义度，也称为损失熵。

定义3.2 称信道输入X条件下，信道输出Y的条件熵

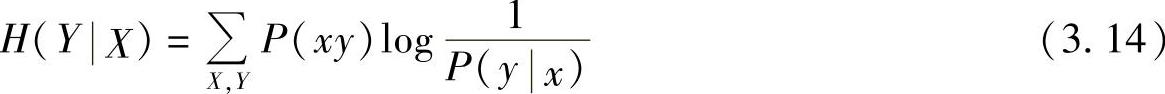
为噪声熵。

信道疑义度H（X|Y）的含义是观察信道的输出Y之后，仍然保留的关于信道输入X的平均不确定度。这种对X尚存在的不确定度是由于传输过程中信道的噪声和干扰引起的。同理，由于信道干扰的存在，一个信道输入符号有可能被正确传输，也有可能被错误传输，所以在信道输入X条件下信道输出Y的平均不确定度，即噪声熵H（Y|X）表征了由于噪声的存在使得收信端收到的信息熵H（Y）中，只有H（Y）-H（Y|X）是信源提供给收信者的信息量，而H（Y|X）是由噪声所提供的信息量。

可见，信道疑义度和噪声熵的存在，均源自于信道干扰。两者从不同的角度衡量了干扰对信息传输的影响。

信道平均每个符号所能传输的信息量是信道的信息传输率。由于平均互信息的含义是接收到符号Y后，平均每个符号获得的关于X的信息量，因此可以给出如下定义：

定义3.3 信道的信息传输率R就是平均互信息，其表达式为

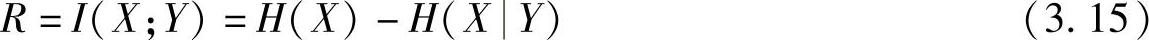
若信道平均传输一个符号为t秒，则信道每秒钟平均传输的信息量，即信息传输速率R_t为

由定义可以知道，信息传输率R的单位是“信息量/符号”，即“bit/符号”或“Nat/符号”等；信息传输速率R_t的单位是“信息量/秒”，即“bit/s”或“Nat/s”等。(www.xing528.com)

可以用图3.12所示关系图形象地表述R=I（X；Y）=H（X）-H（X|Y）=H（Y）-H（Y|X）。其中：

图3.12a是一般信道上信息的传输情况，通常信道疑义度和噪声熵都不为0。

图3.12b表明，无损信道将信源送入的信息全部传输到收信端，收信端获得信源提供的全部信息，对信源不存在任何疑问（信道疑义度为0）。但由于信道噪声使得收到的消息中既有信源的全部信息，也有信道噪声传输到收信端的噪声熵（由信道产生）。

图3.12c表明，无噪信道将信源送入的部分信息传输到收信端（部分信息损失在信道中，收信端对信源仍存部分不确定度，信道疑义度不为0），由于信道无噪声（噪声熵为0），收信端收到的信息全部来自信源。

图3.12d表明，无噪无损信道将信源送入的信息全部传输到收信端，且收信端收到的信息全部来自信源。此时，信道疑义度和噪声熵都为0。

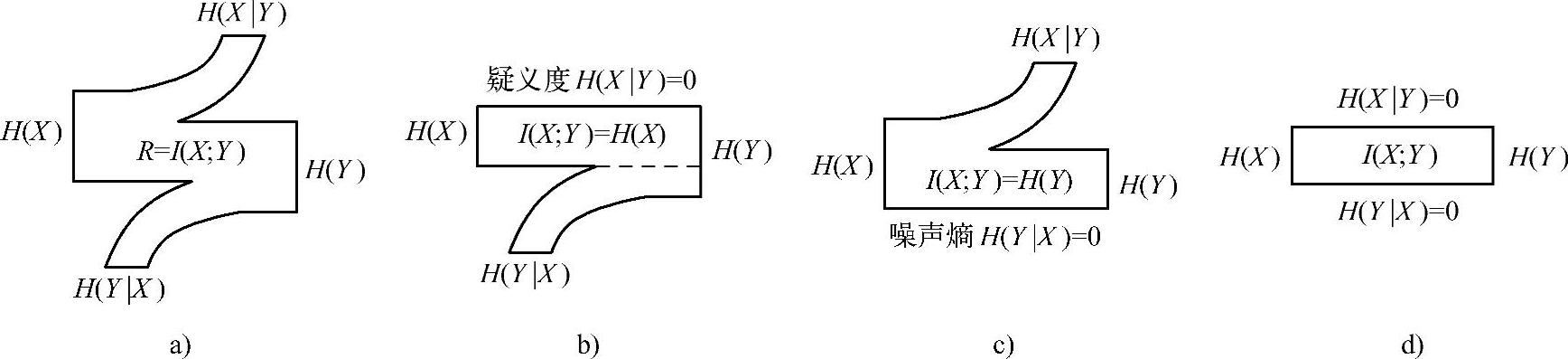
图3.12 信道两端的熵关系

a）一般信道 b）有噪无损信道 c）无噪有损信道 d）无噪无损信道

下面再举一个学习的例子说明信息的传输问题。

【例3.2】

教师在教学过程中讲述了所授课程的全部知识。

如果教室很安静，学生基础扎实且认真听课，则学生接受了全部知识。此时，可以看成是无噪无损的信道情况。

如果学生基础不很扎实，但教室很安静，尽管学生听清了教师的授课内容，并没有接受教师所教授的全部知识。此时，可以看成是无噪有损的信道情况。

如果学生基础很扎实，但教室不很安静，学生能将听到的授课内容（因噪声，接收到的消息有一定的错误，即噪声熵不为0）中正确的知识全部接受，但不是教师授课的全部知识。此时，可以看成是有噪无损的信道情况。

最一般的情况是学生基础不很扎实，教室也不很安静，教师讲的内容学生不能完全听清楚，听清楚的也不能全理解。此时，可以看成是一般的有噪有损的信道情况。

由平均互信息的非负性表明“只要学习了，总是增加知识的”。不可能在学习的过程中，将所掌握的知识变少。尽管有时一时的疏忽导致增加了一些困惑，只要系统地学完一方面的知识，则我们的能力一定是提高的。