连续信道的数学模型优化：

在2.6.1节中分析了连续信源的3种表示方法，并给出了波形信源、多维连续信源和基本连续信源的概念。将这3种连续信源应用于连续信道，也就产生了相应的3种连续信道。

1.波形信道

当信道的输入和输出都是随机过程{x（t）}和{y（t）}时，即输入和输出都是模拟随机信号x（t）和y（t）时，这个信道称为波形信道，又称为模拟信道。波形信道模型如图3.9所示，其中，作用于信道上的随机过程{n（t）}是噪声过程。

实际模拟通信系统中，信道都是波形信道。工程上波形信道的频带宽度总是有限的，如一路模拟电话的频带宽度为3.4 kHz，中波广播的频带范围为100～1500 kHz，短波广播的频带范围为6～30 MHz，分米波的移动通信频带范围为300 MHz～3 GHz等。所以，实际信道在有限观察时间内，能满足限时T、限频F的条件。因此，可以根据取样定理把波形信道的输入{x（t）}和输出{y（t）}的平稳随机过程离散化成N（=2FT）个时间离散、取值连续的平稳随机序列X=（X₁，X₂，…，X_N）和Y=（Y₁，Y₂，…，Y_N），这就产生了多维连续信道。

2.多维连续信道

N维连续信道的模型如图3.10所示。信道的输入是N维连续型随机序列X=（X₁，X₂，…，XN），输出也是N维连续型随机序列Y=（Y₁，Y₂，…，Y_N），而信道转移概率密度函数是p（y|x）=p（y₁y₂…y_N|x₁x₂…x_N），并且满足

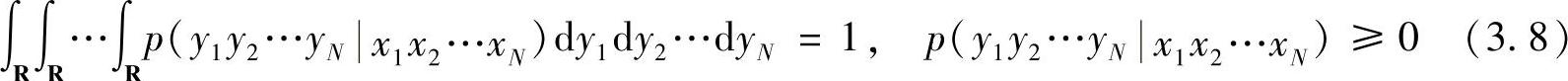
可以用[X，p（y|x），Y]来描述N维连续信道。式中，R为实数域。

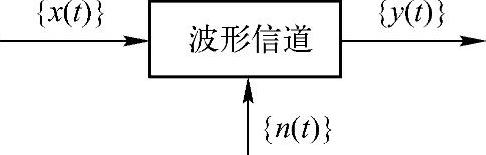
图3.9 波形信道

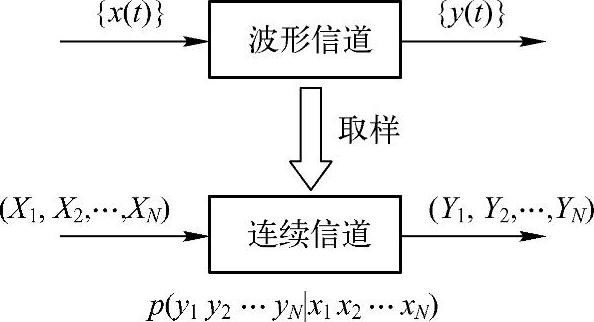
图3.10 波形信道转化成多维连续信道

若N维连续信道的转移概率密度函数满足

则称此信道为连续无记忆信道。

与离散无记忆信道的定义一样，若连续信道在任一时刻输出的变量只与对应时刻的输入变量有关，与以前时刻的输入、输出变量无关，也与以后的输入变量无关，则此信道是连续无记忆信道。

一般情况下式（3.9）不满足，也就是连续信道任一时刻的输出变量与其他任何时刻的输入、输出变量都有关，则称此信道为连续有记忆信道。

3.基本连续信道

基本连续信道就是输入和输出都是单个连续型随机变量的信道，也称为连续单符号信道，信道模型如图3.11所示。该信道的输入是连续型随机变量X，其值域为（a，b）或实数域R；输出也是连续型随机变量Y，其值域为（a′，b′）或实数域R；信道转移概率密度函数为p（y|x），并满足(www.xing528.com)

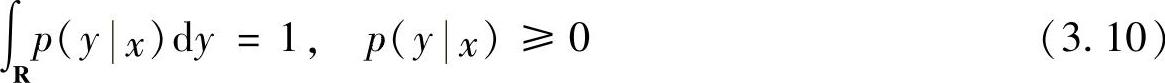
因此，可以用[X，p（y|x），Y]来描述基本连续信道（连续单符号信道）。

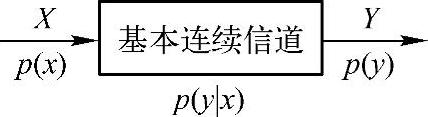
图3.11 基本连续信道

4.半离散半连续信道

信道的输入符号取自有限的、离散的输入符号集A：{a₁，a₂，…，a_r}，而信道的输出未经量化（s→∞），这时信道的输出符号的值域为实数域R或其子集（a′，b′）。这种信道称为半离散半连续信道，它的特性由离散输入X、连续输出Y，以及一组条件概率密度函数p（y|X=a_i）（i=1，2，…，r）来决定。

根据噪声对信道中信号的作用不同，可以将噪声分为加性噪声和乘性噪声，即噪声与输入信号是相加或相乘得到输出信号。一般分析较多的，而且也容易从理论上进行分析的是加性噪声信道。加性噪声信道可以表示为

y（t）=x（t）+n（t）

式中，n（t）是加性噪声过程的样本函数。通常噪声和信号是相互独立的，所以

p_X，Y（x，y）=p_X，n（x，n）=p_X（x）p_n（n） （3.11）

则

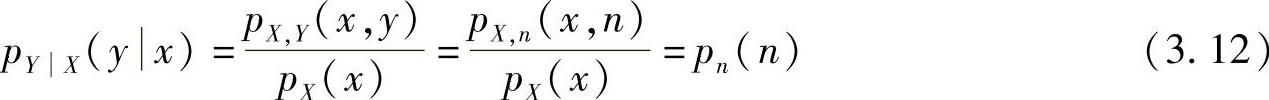
即加性噪声信道转移概率密度函数等于噪声的概率密度函数。这说明了信道转移概率是由噪声引起的。

以后还可以证明在加性噪声信道中，条件熵是由信道中噪声引起的，它完全等于噪声信源的熵，所以称为噪声熵。以后主要讨论加性噪声信道，噪声源主要是高斯白噪声。

以上只讨论了一些常见信道模型的参数，并没有完全讨论所有类型的信道。在不同的研究中会用到不同的信道模型：

1）设计和分析离散信道编、解码器的性能时，从工程角度出发，最常用的是DMC信道模型，或其简化形式BSC信道模型。

2）分析性能的理论极限时，则多选用离散输入、连续输出信道模型。

3）设计和分析数字调制器和解调器的性能时，则可以采用连续的波形信道模型。