【摘要】：但是，由于连续信源存在多个概念上的最大信源熵，使得其信源效率的衡量不能完全借鉴离散信源的方法。因此，信息论中衡量连续信源的效率问题就以平均功率受限条件下的熵为标准。由2.6.4节已知，当信号平均功率受限时，高斯分布信源的差熵最大。为此，给出如下定义：定义2.28 若平均功率为P的非高斯分布的信源具有熵h，称熵也为h的高斯信源的平均功率为熵功率P。只有高斯分布的信源的熵功率等于实际平均功率，其冗余度为零。
离散信源存在唯一的最大熵定理，因此，可以用其最大熵作为标准来衡量离散信源的效率，并引出了离散信源的冗余度和相对率的概念。但是，由于连续信源存在多个概念上的最大信源熵，使得其信源效率的衡量不能完全借鉴离散信源的方法。
鉴于高斯信号是工程中最重要的一种信号。因此，信息论中衡量连续信源的效率问题就以平均功率受限条件下的熵为标准。这就引出了连续信源的熵功率的概念。
由2.6.4节已知，当信号平均功率受限时，高斯分布信源的差熵最大。令其平均功率为P，则其熵为
如果另一信源的平均功率也为P，但不是高斯分布，那它的熵一定比式（2.132）计算的值小。为此，给出如下定义：
定义2.28 若平均功率为P的非高斯分布的信源具有熵h，称熵也为h的高斯信源的平均功率为熵功率P。即熵功率是(www.xing528.com)
因为当平均功率受限时，一般信源的熵小于高斯信源的熵，所以信号的熵功率总是小于等于信号的实际功率P，即
可见，信号功率与熵功率的接近程度表示了连续信源冗余的大小。如果熵功率等于信号平均功率，就表示信号没有冗余。信号功率与熵功率相差越大，说明信号的冗余越大。
定义2.29 信号的平均功率P与熵功率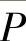
之差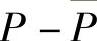
称为连续信源的冗余度。
只有高斯分布的信源的熵功率等于实际平均功率，其冗余度为零。这就是高斯噪声信源。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
