基本连续信源的熵分析

基本连续信源（即连续单符号信源）是波形信源经取样后的某一维，其数学模型为

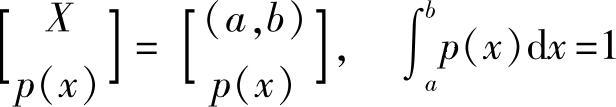或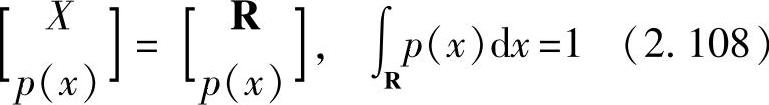

假定基本连续信源的概率密度函数p（x）如图2.9所示。把连续随机变量X的取值分割成n个小区间，各小区间等宽，即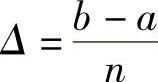，则变量落在第i个小区间的概率为

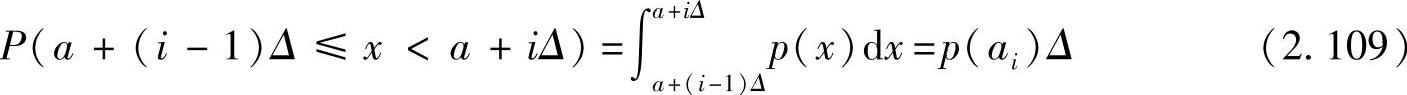
其中，a_i是区间[a+（i-1）Δ，a+iΔ）中的某个值。当p（x）是x的连续函数时，由中值定理可知，必存在某个a_i使式（2.109）成立。这样连续随机变量X就可以用取值为a_i（i=1，2，…，n）的离散随机变量X_n来近似，且每个符号a_i的概率为p（a_i）Δ。这样，连续信源就被量化成离散信源，该离散信源熵为

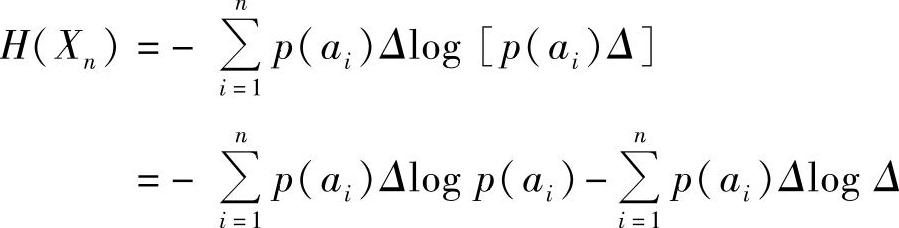
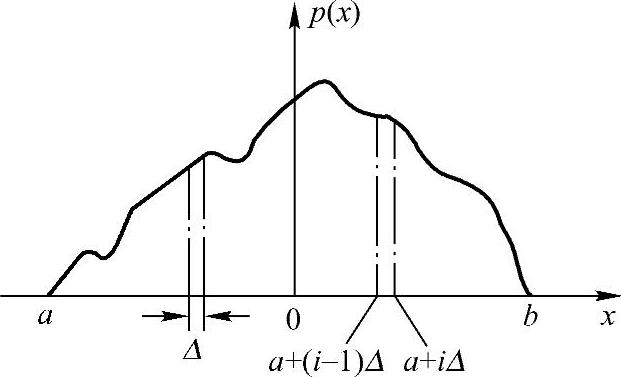
图2.9 概率密度函数

当n→∞时，Δ→0，离散随机变量X_n趋于连续随机变量X，而离散信源X_n的熵H（X_n）的极限值就是基本连续信源的信息熵

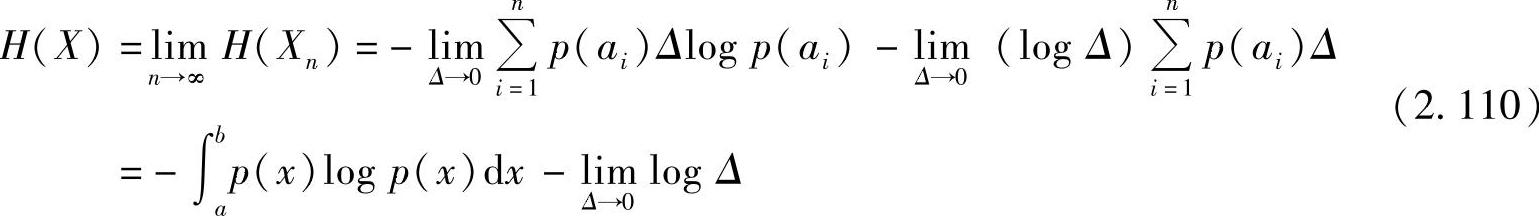
式（2.110）中的第一项是定值，具有离散信源熵的形式；第二项是趋于无限大的常数（依赖于Δ）。所以避开第二项，定义连续信源的信息熵如下：

定义2.23 设连续随机变量X的概率密度函数为p（x），称

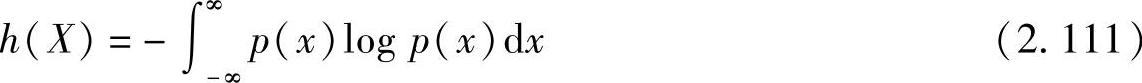
为该连续信源的熵，也称为差熵（或相对熵、微分熵）。

连续信源的熵与离散信源的熵具有相同的形式，但其意义不同。连续信源的不确定度应为无穷大，这是因为连续信源有不可数的、无限多个幅度值的信源，需要用无限多个二进制位数（bit）来表示，所以它的实际熵为无穷大。但采用式（2.111）来定义的连续信源的熵是因为在实际问题中，常遇到的是熵之间的差值，如互信息量，只要两者逼近时所取的Δ一致，式（2.110）中的第二项无穷大量是抵消的。

由此可见，连续信源的熵具有相对性，这也是称其为差熵、相对熵和微分熵的原因。

【例2.36】

有一连续信源的概率密度如图2.10所示。由图2.10a得(www.xing528.com)

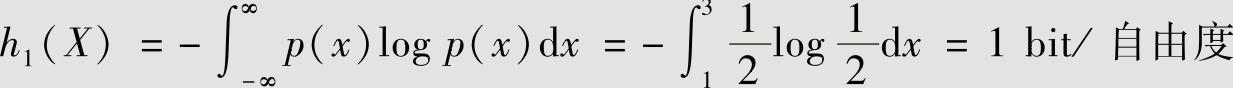
由图2.10b得

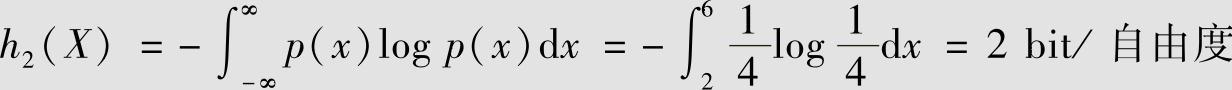
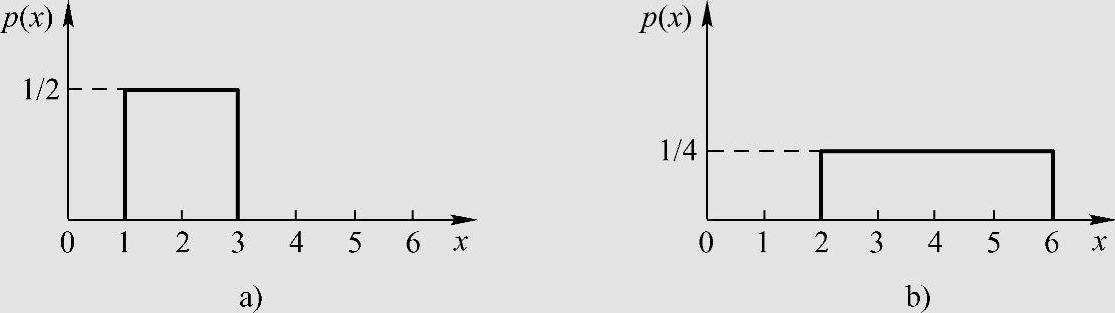
图2.10 例2.36的概率密度函数

a）信源输出信号的概率密度 b）输出信号被放大2倍的概率密度

图2.10b是图2.10a放大2倍的结果，计算表明信息量增加了，这是荒谬的。因为两种情况的实际熵是不会变的。这是由于无穷大项所造成的，两者逼近时所取的Δ不一致，图2.10b比图2.10a小1 bit。因此，h（X）给出的熵有相对意义，而不是绝对值。

用上述方法可以定义两个连续随机变量X和Y的各种熵。

定义2.24 在连续联合随机变量集XY上，其联合熵为

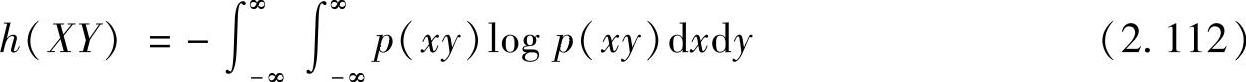
式中，p（xy）为二维联合概率密度函数。

定义2.25 在连续联合随机变量集XY上，其条件熵为

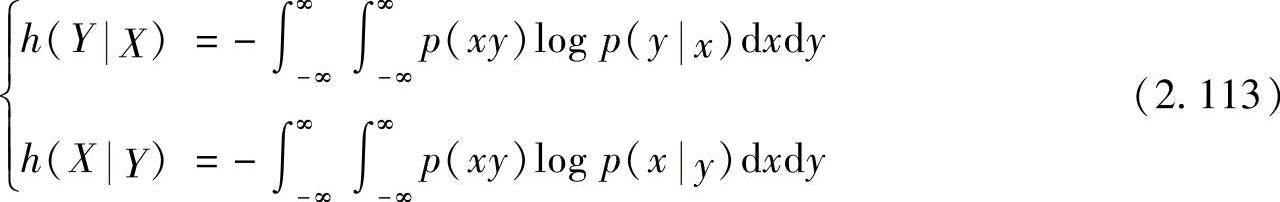
式中，p（y|x）和p（x|y）为条件概率密度函数。

定义2.26 在连续联合随机变量集XY上，两个连续随机变量的平均互信息为

式（2.111）～式（2.113）定义的连续信源的熵虽然在形式上与离散信源的熵相似，但在概念上不能把它作为信息熵来理解。但式（2.114）定义的平均互信息却是与离散随机变量的概念相同。