如何表述连续信源

常见的语音信号、声音信号、视频信号、广播信号和电视信号等都是波形连续的信号。这类信号与文字、符号等有限字符集的离散信号有很大的区别，其特点是信号的幅值是连续的和随机的，且是时间的连续函数，其值可以取自定义区间内的任意值，有不可数的无穷多种可能取的值。这是一类时间连续的模拟信号，也称为波形信号。

在实际中，波形信号总是限时和限频的。一个时间连续、幅度连续，并满足限时T、限频F的模拟信号x（t）可以有下列3种表示方法：

1）时间连续、取值连续的波形信号x（t）。

2）根据奈奎斯特取样定理，将x（t）离散化成2FT个时间离散、取值连续的取样序列x（t₁），x（t₂），…，x（t_2FT）。

3）对取样序列中的某一维的取样值x（t_i）进行分析。

将这3种处理模拟信号的方法用于连续信源，相应地会得到3种连续信源的表述方法。

1.波形信源

直接以模拟信号的波形来描述的信源称为波形信源，这是一种输出信号在时间上连续，幅值上也连续的信源，可以用随机过程{x（t）}来表示。随机过程{x（t）}中的每一个样本函数x（t）是该信源输出的一个连续消息。

例如，音频信号的频带为20Hz～20kHz，电话语音通信信号的频带为300～3400 Hz等。可见，波形信源在有限观察时间内，能满足限时T、限频F的条件。因此，可以根据奈奎斯特取样定理，把波形信源输出的平稳随机过程{x（t）}离散化成N（=2FT）个时间离散、取值连续的平稳随机序列X=（X₁，X₂，…，X_N），这就产生了多维连续信源。

2.多维连续信源

N维连续信源是从波形信源经过取样得到的，该信源输出的消息为N维连续型随机序列X=（X₁，X₂，…，X_N），并由N维概率密度函数p（x）=p（x₁x₂…x_N）来描述N维连续信源，并且满足

式中，R为实数域。若N维连续信源的概率密度函数满足(www.xing528.com)

则称此信源为连续无记忆信源。但遗憾的是，很多连续信源都是有记忆的。

3.基本连续信源

基本连续信源就是单个连续型随机变量的信源，也称为连续单符号信源。它可以看成是波形信源经取样后的某一维所构成。该信源输出的消息为连续型随机变量X，值域为（a，b）或实数域R；用概率密度函数p（x）来描述，并满足

就统计特性而言，连续随机过程大致可以分为平稳随机过程和非平稳随机过程两大类。前者是指统计特性（各维概率密度函数）不随时间平移而变化的随机过程，后者则是统计特性随时间平移而变化的随机过程。

一般认为，通信系统中信号都是平稳的随机过程。虽然在无线通信系统中，受衰落干扰的无线电信号属于非平稳随机过程，但在正常通信条件下，都可以近似地当作平稳随机过程或短时平稳的随机过程来处理。

在随机过程{x（t）}中，某一样本函数x（t）的时间平均值定义为

而集平均是随机过程{x（t）}在某时刻t_i所取的随机变量X_ti的统计平均值

最常见的平稳随机过程都是遍历过程。所以，常用平稳遍历的随机过程来描述连续信源。遍历的随机过程的定义如下：

定义2.22 若随机过程{x（t）}的统计特性不随时间变化，且其集平均还以概率1等于时间平均，即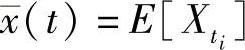，则称{x（t）}为遍历的随机过程。

本节仅讨论具有平稳遍历特性的连续信源（随机过程）的熵。