信息论基础：马尔可夫信源的熵

在非平稳离散信源中有一类特殊的信源，这类信源输出的符号序列中符号之间的记忆关系是有限的，它满足马尔可夫链的性质，因此可以用马尔可夫链来处理，并求出此信源的信息熵。本节将讨论这类信源。

1.马尔可夫链和马尔可夫信源的定义

一般情况下，信源输出的符号序列中符号之间的记忆关系是有限的，即任一时刻信源符号发生的概率只与前面已经输出的若干个符号有关，而与更前面输出的符号无关。对于这种情况，可以认为信源在某一时刻发出的符号与信源所处的状态有关。

设信源X的状态集为E：{e₁，e₂，…，e_n}，在每一状态下信源X可能输出的符号集为A：{a₁，a₂，…，a_r}。且每一时刻当信源发出一个符号后，信源所处的状态将发生变化，并转入一个新状态。信源输出的随机符号序列为x₁，x₂，…，x_t，…（x_t∈A；t=1，2，…）；信源在初始状态s₀条件下，相对应的随机状态序列为s₁，s₂，…，s_t，…（s_t∈E；t=1，2，…）。由于马尔可夫信源是一种具有马尔可夫链性质的信源，为此，先给出马尔可夫链的定义，再讨论马尔可夫信源的定义。

定义2.18 若状态序列s₀，s₁，s₂，…，s_t，…（s_t∈E：{e₁，e₂，…，e_n}；t=0，1，2，…）（s₀为初始状态）满足下列两个条件：

1）有限性：可能的状态数n＜∞，即只有有限个可能的状态。

2）马尔可夫性：系统的下一个状态只与当前的状态有关，与更早的状态无关，即

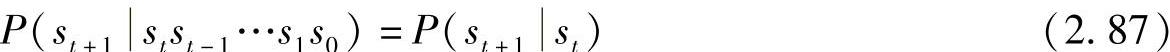
则称该随机状态序列为有限状态马尔可夫链（简称马尔可夫链），称P（s_t+1s_t）为状态转移概率（或一步状态转移概率）。若P（s_t+1s_t）与时刻t（时间推移）无关，即满足

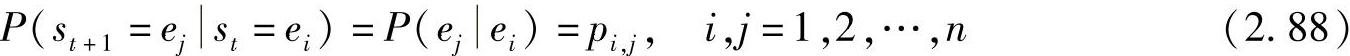
则称该随机状态序列为时齐（或齐次）马尔可夫链（或时齐的、齐次的）。

定义2.18条件2表明，马尔可夫链中将要出现的状态只与它前面的一个状态有关，体现了状态和状态之间的“一环扣一环”的性质，这也是称为“链”的由来。下面仅分析时齐马尔可夫链。一般描述马尔可夫链的数学工具是状态转移矩阵和状态转移图。

因为所有可能的状态有n个，所以时齐马尔可夫链共有n×n个状态转移概率p_i，j。为表述方便，可以用状态转移矩阵P表示这些转移概率，其表达式为

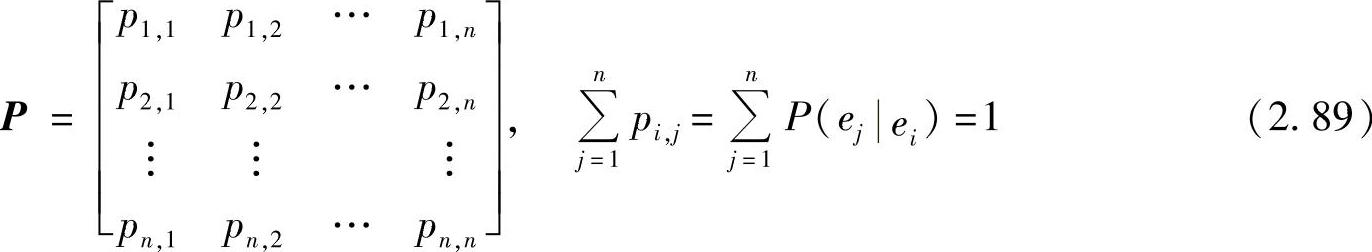
概率p_i，j还可以用图形化的方式表示，如图2.5所示。该图称为状态转移图，表示由状态e_i一步转移到状态e_j的概率是p_i，j。状态转移矩阵P中所有元素都可以表示为图2.5所示的样子，所有的状态之间的转移关系连在一起，构成了整个系统状态转移图（见例2.31和例2.32）。

定义2.19 对于有限状态马尔可夫链，若存在一个正整数k≥1，对一切i，j∈{1，2，…，r^m}，都有P_k（e_je_i）＞0，则称该马尔可夫链是各态遍历的。其中，P_k（e_je_i）是由状态e_i经k步转移到状态e_j的k步状态转移概率。

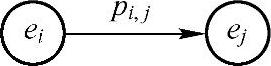
图2.5 状态转移图

遍历性是马尔可夫链的重要性质之一。对于时齐、遍历的马尔可夫链，其状态具有平稳分布的特点，可以用时齐性和遍历性求解一类马尔可夫信源的熵。

定义2.20 若信源X输出的符号序列x₁，x₂，…，x_t，…（x_t∈A；t=1，2，…）和状态序列s₀，s₁，s2，…，s_t，…（s_t∈E；t=0，1，2，…）（s₀为初始状态）满足下列两个条件：

1）信源输出的下一个符号只与当前的信源状态有关，而与以前的状态及以前输出的符号无关，即^[3]

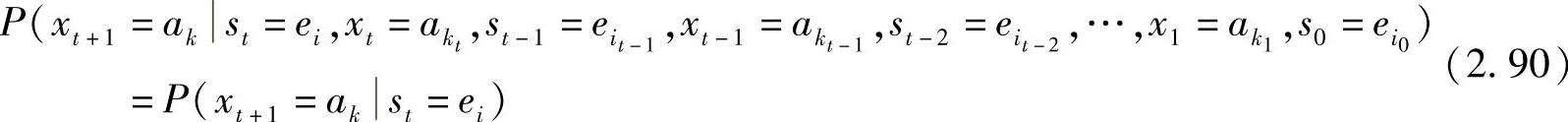
其中，k_t+1（=k），k_t，k_t-1，…，k1∈{1，2，…，r}；i_t（=i），i_t-1，i_t-2，…，i0∈{1，2，…，n}。

2）当前信源的状态和输出的下一个符号唯一地确定信源的下一个状态，即

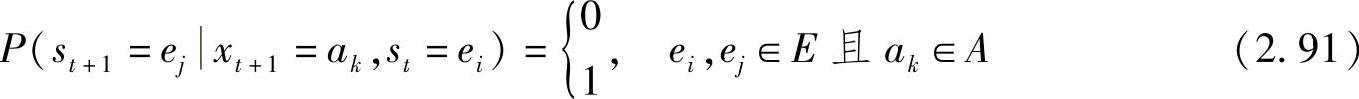
则称此信源为马尔可夫信源。若概率P（x_t+1=a_ks_t=e_i）与时刻t（时间推移）无关时，即满足

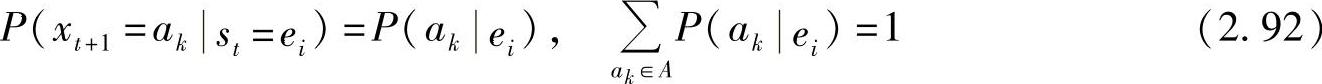
则此信源称为时齐（或齐次）马尔可夫信源。

需要指出的是，平稳信源的概率分布特性具有时间推移不变性，齐次马尔可夫信源只要求转移概率具有时间推移不变性。因此，平稳性包含齐次性，但齐次性不包含平稳性。

定义2.20表明，信源输出的符号序列x₁，x₂，…，x_t，…（x_t∈A；t=1，2，…）完全由信源所处的状态s_t决定，故可以将信源输出的符号序列变换成信源的状态序列s₁，s₂，…，s_t，…（s_t∈E；t=0，1，2，…）。于是将信源输出符号的不确定度问题变换成信源的状态转换的问题。从定义还可以看出，若信源在时刻t处于某一状态e_i（e_i∈E：{e₁，e₂，…，e_n}），当信源发出一个符号a_k（a_k∈A：{a₁，a₂，…，a_r}）后，所处的状态就变了，从e_i状态变成e_j状态。显然，信源状态的转移依赖于信源发出的符号和所处的状态。状态之间的状态转移概率为

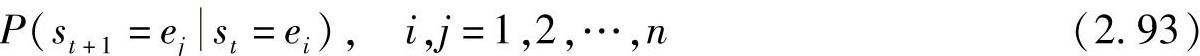
式（2.93）表示信源在时刻t处于e_i状态，在下一时刻t+1状态转移到e_j的一步状态转移概率。

马尔可夫信源在数学上可以用马尔可夫链来处理。因而，可以用马尔可夫链的状态转移图来描述马尔可夫信源。在状态转移图上，把n个可能的状态中的每一个状态用一个圆圈表

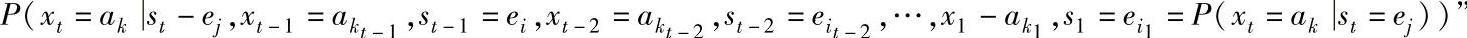
其条件概率P（x_t=a_k|s_t=e_j）的含义是：在当前状态s_t=e_j下，输出当前的信源符号x_t=a_k。这与本书的写法不完全相同。请读者注意其中的差别。示，然后它们之间用有向线连接，以此表示信源输出某符号后，由某一状态到另一状态的转移。并把输出的符号a_k及条件概率P（a_ke_i）标注在有向线的一侧。

【例2.31】

信源X的值域为A：{a₁，a₂，a₃}，信源所处的状态集为E：{e₁，e₂，e₃，e₄}。各状态之间的转移情况由图2.6给出。由图可知，e_i状态下输出符号的概率分别为

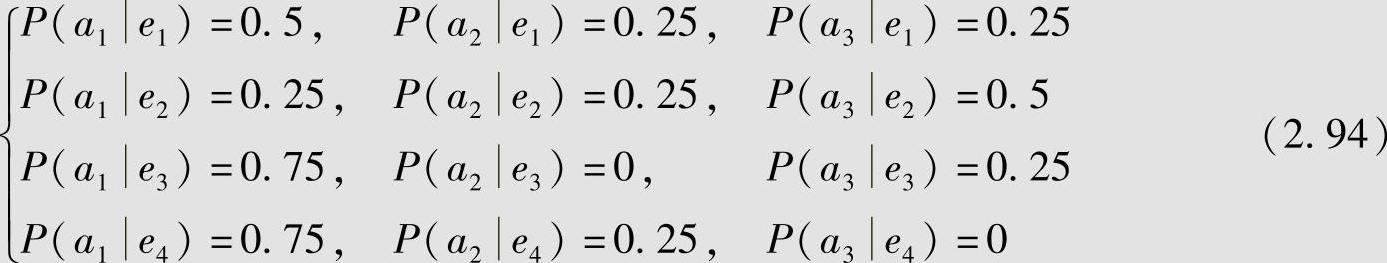
可见，满足关系式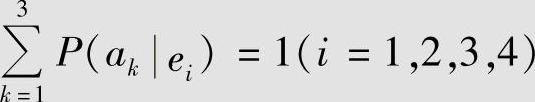。从图中还可以得到

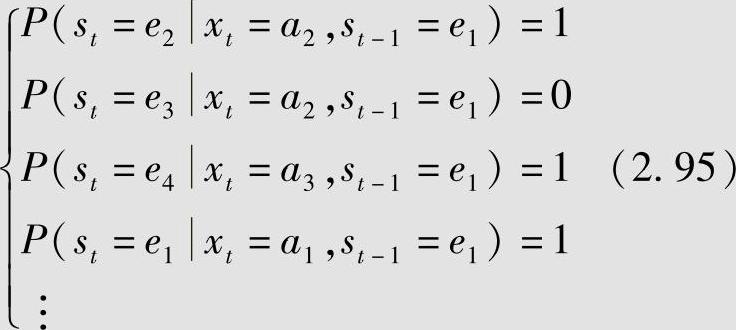
所以，信源满足条件式（2.91）。

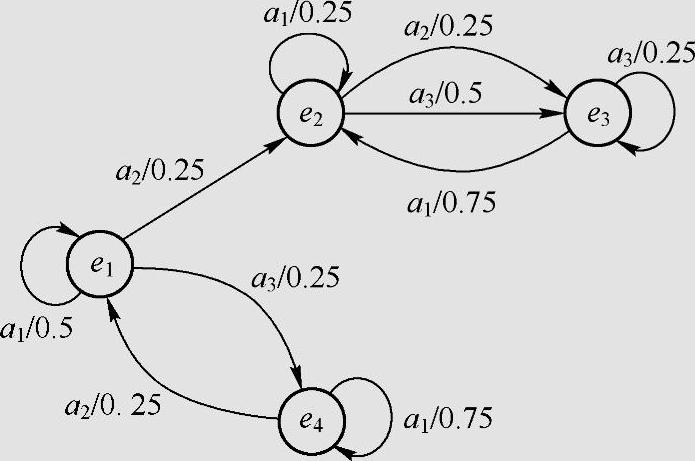
图2.6 例2.31的状态转移图

根据式（2.94）和式（2.95），可以求得状态的一步转移概率为

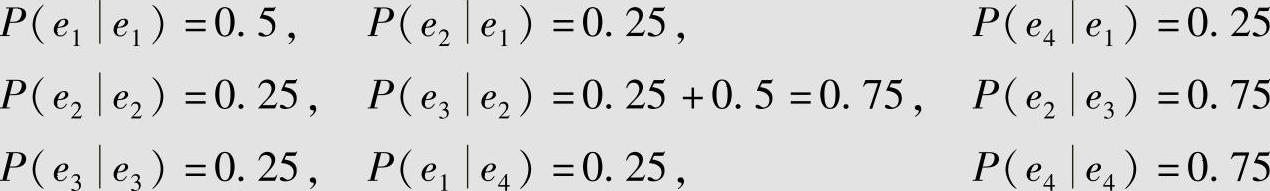
其余P（e_je_i）=0。可见，此信源满足条件式（2.90）～式（2.92），所以该信源是时齐马尔可夫信源。还可以从图2.6的状态转移图中看到，没有从状态e₂和e₃转移到状态e₄的通路，因此该马尔可夫信源不是遍历的。

2.m阶马尔可夫信源的定义

定义2.20给出了一般的马尔可夫信源的定义。但常见的一些马尔可夫信源，其可能的状态与符号序列有关。如m阶离散有记忆信源在任一时刻t，符号发生的概率只与前面m个符号有关，可以把这前面m个符号序列看作信源在时刻t所处的状态。因为信源符号集共有r个符号，则信源可以有r^m个不同的状态，它们对应于r^m个不同的符号序列。这时，信源输出的记忆长度为m+1的随机序列就可以转换成对应的状态随机序列，而这状态序列符合马尔可夫链的性质。因此，m阶离散有记忆信源可以用马尔可夫链来描述。

定义2.21 m阶离散有记忆信源的数学模型可以由一组信源符号集A：{a₁，a₂，…，a_r}和一组条件概率确定

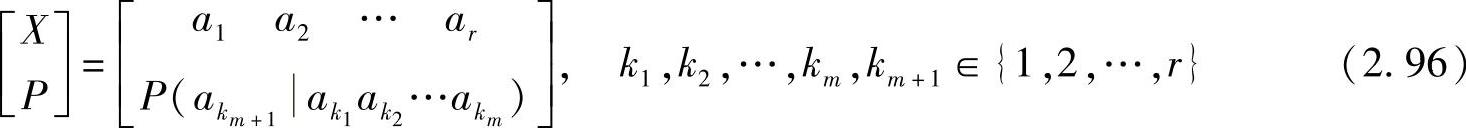
并满足

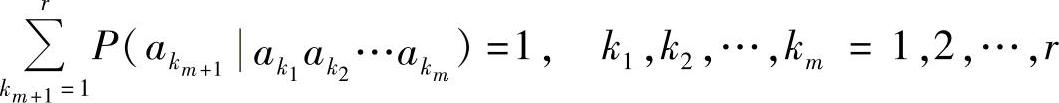
则称此信源X为m阶马尔可夫信源。

m阶马尔可夫信源X在任一时刻t，符号发生的概率只与前m个符号有关，可以设状态为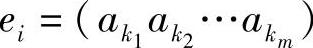，信源X的状态集为E：{e₁，e₂，…，e_n}，n=r^m。因此，条件概率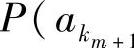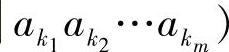可以变换成

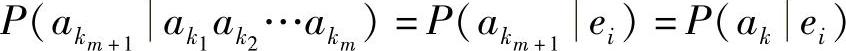，k=1，2，…，r且i=1，2，…，r^m（2.97）式中，条件概率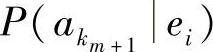表示在任一时刻t信源处于状态e_i时输出下一个符号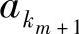的概率，。可见它满足式（2.90）。而且，当在时刻t信源输出符号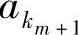后，由符号序列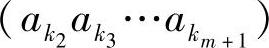组成了新的信源状态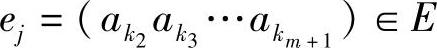，信源所处的状态也由e_i转移到e_j。所以，它也满足条件式（2.91）。状态之间的一步转移概率P（eje_i）也可以由条件概率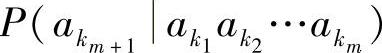来确定。

因此，m阶马尔可夫信源符合一般马尔可夫信源的定义。然而，m阶马尔可夫信源又是一种常见的、简单的马尔可夫信源。当m=1时，一阶马尔可夫信源是最简单的马尔可夫信源。

【例2.32】(www.xing528.com)

二元二阶马尔可夫信源X的值域为A：{0，1}，条件概率为

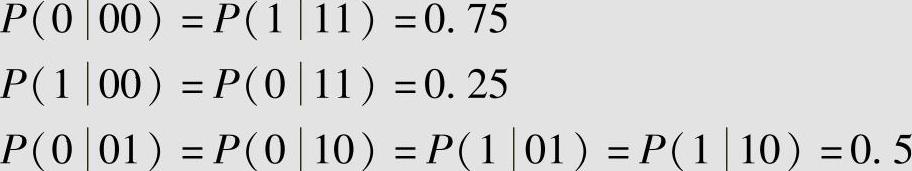
求该信源的状态转移概率和状态转移图。

解 该信源共有r^m=2²=4种可能的状态：e₁=00，e₂=01，e₃=10，e₄=11。如果信源原来所处e₁=00状态，因为信源只能发出符号0或1，故下一时刻信源只可能转移到e₁=00或e₂=01状态，而不会转移到其他状态。同时，也可以分析出初始状态为其他状态时的状态转移过程。由条件概率容易求得一步状态转移概率为

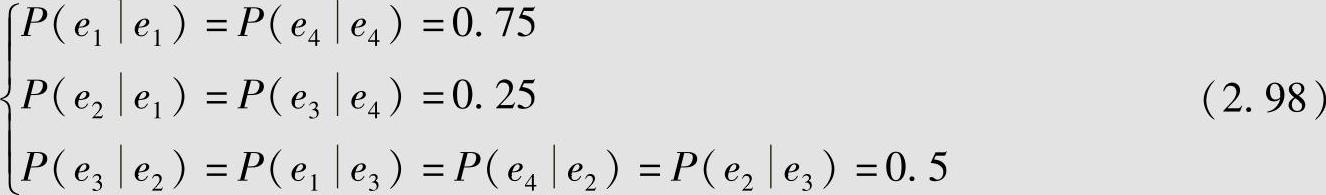
其余的一步状态转移概率为零。该信源的状态转移图如图2.7所示。由此可见，状态转移概率完全依赖于给定的条件概率。还可以从图2.7的状态转移图中看到，所有的状态都可以相互转移到，因此该马尔可夫信源是遍历的。

【例2.33】（续例2.32）

假设二元序列…01100101100100…是图2.7所示的二阶马尔可夫信源发出序列的一部分，试将该部分的二元序列变换成对应的状态序列。

解 取序列的第1、2个符号01，得到对应的状态e₂；再取第2、3个符号11，得到对应的状态e₄；再取第3、4个符号10，得到对应的状态e₃……一直进行到序列结束，可得到该二元序列对应的状态序列为…e₂e₄e₃e₁e₂e₃e₂e₄e₃e₁e₂e₃e₁…。这串状态序列是时齐的马尔可夫链，其在任一时刻t，状态之间的转移概率由状态转移概率式（2.98）确定。

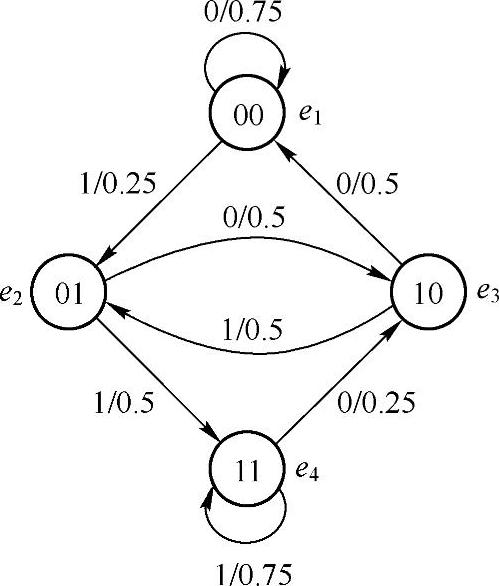
图2.7 二阶马尔可夫信源状态转移图

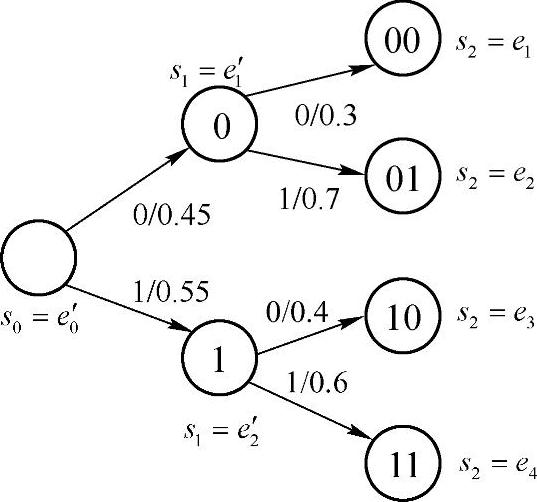
图2.8 例2.34的状态转移图（t=1，2）

【例2.34】（续例2.32）

在例2.32的二阶马尔可夫信源中，起始时的状态转移图如图2.8所示。信源在t=1时刻以初始概率P（0）=0.45，P（1）=0.55输出随机变量X₁；在t=2时刻以条件概率P（0|0）=0.3，P（1|0）=0.7，P（0|1）=0.4，P（1|1）=0.6输出随机变量X₂；在以后时刻信源以例2.32中的二阶条件概率输出信源符号。计算经过1、2、3次状态转移后的信源符号的概率分布和信源的状态转移过程。

解 马尔可夫信源在起始运动时，以初始状态s₀=e₀′开始，有一个过渡过程。

1）在t=1时刻信源以概率P（0）=0.45输出符号0，进入状态s₁=e′₁；或以概率P（1）=0.55输出符号1，进入状态s₁=e₂′。此时（时刻t=1），信源符号0和1出现的概率分别为

P^（1）（0）=P（0）=0.45

P^（1）（1）=P（1）=0.55

信源系统处于各状态的概率为

P^（1）（s₁=e₁′）=P（0）=0.45

P^（1）（s₁=e₂′）=P（1）=0.55

2）在t=2时刻，①信源从t=1时刻的状态s₁=e′₁以概率P（0|0）=0.3输出符号0，进入状态s₂=e₁；或以概率P（1|0）=0.7输出符号1，进入状态s₂=e₂。②信源从t=1时刻的状态s₁=e₂′以概率P（0|1）=0.4输出符号0，进入状态s₂=e₃；或以概率P（1|1）=0.6输出符号1，进入状态s₂=e₄。此时（时刻t=2），信源已包含全部4个可能状态s₂∈{e₁，e₂，e₃，e₄}，信源符号0和1出现的概率分别为

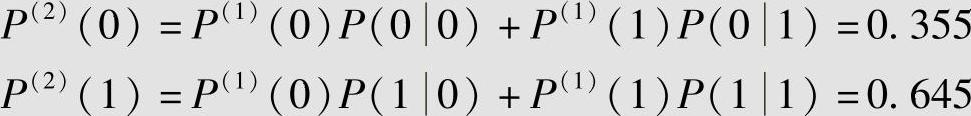
信源系统处于各状态的概率为

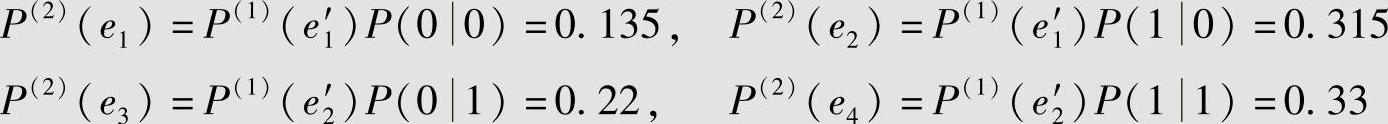
3）从t=3时刻开始，信源以图2.7的状态转移图进行转移。在t=3时刻信源符号0和1出现的概率分别为

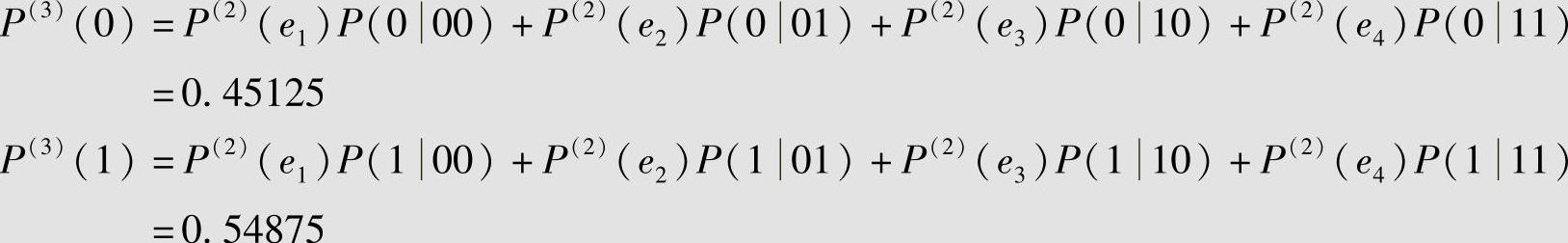
信源系统处于各状态的概率为

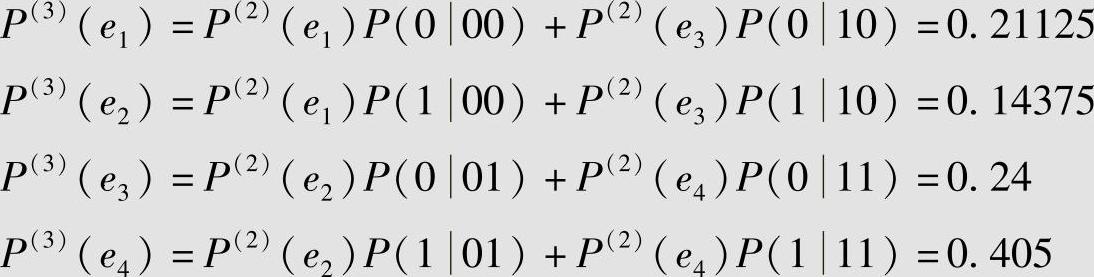
从例2.34的结果可以看到，尽管时齐马尔可夫信源的条件概率与时间推移无关，是平稳的，但其信源输出的符号序列和信源的状态序列仍然是不平稳的。

可以证明，对于遍历、时齐马尔可夫信源，当状态转移步数足够长以后状态的极限概率分布存在，并且与初始的状态概率分布无关。这意味着遍历、时齐马尔可夫信源在初始时可以处在任意状态，然后状态之间可以互相转移。经过足够长时间之后，信源处于什么状态已与初始状态无关，这时信源每种状态出现的概率已达到一种稳定分布Q（e_j）（e_j∈E）。这类信源在起始的有限时间内输出的符号序列可能是不平稳的，状态的概率分布有一段起始渐变过程。但经过足够长的时间之后，状态概率才达到一种稳定分布，此时，信源输出的序列是平稳序列。

下面的定理（证明略）给出了遍历、时齐马尔可夫信源的极限概率分布的求解方法。

定理2.2（各态遍历定理）遍历、时齐马尔可夫链存在下列（状态）极限概率Q（e_j）：

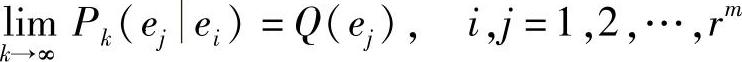
且极限概率是下列方程组的唯一解：

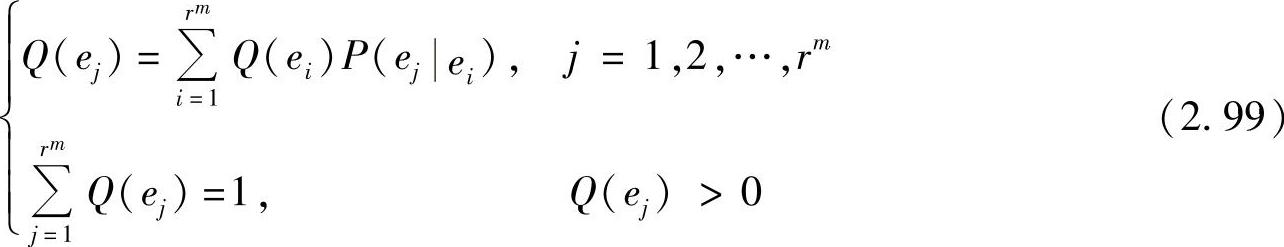
3.m阶马尔可夫信源的熵

由前面的分析可知，当时间足够长后，遍历、时齐的m阶马尔可夫信源可以视为平稳信源来处理。又因为信源发出的符号只与最近的m个符号有关，所以根据式（2.82）可得

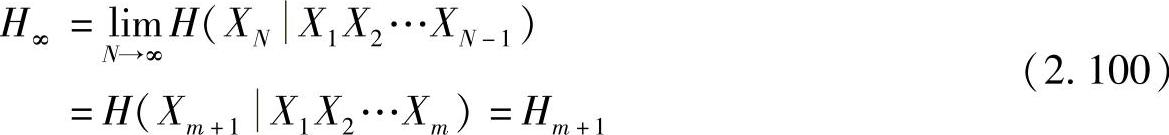
即m阶马尔可夫信源的极限熵H_∞等于m阶条件熵。

下面计算H_m+1。

对于遍历、时齐马尔可夫信源，其状态e_j由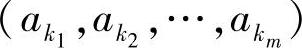唯一确定，因此有

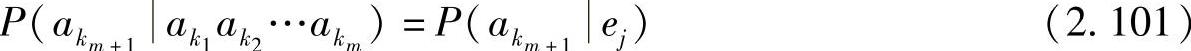
式（2.101）两端同时取对数，并对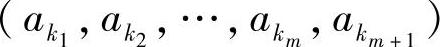和e_j取统计平均，然后取负，得

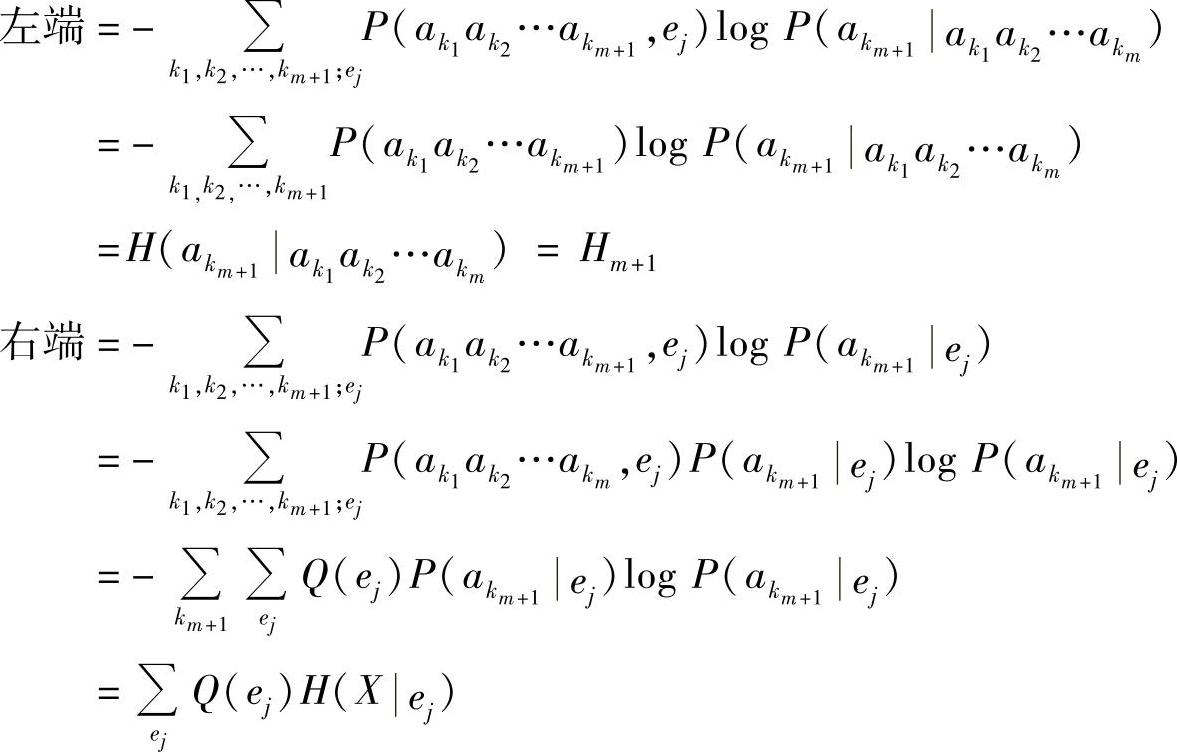
亦即

式中，Q（e_j）是马尔可夫链的平稳分布，它可以根据定理2.2给出的方法计算。熵函数H（X e_j）表示信源处于某一状态e_j时发出一个消息符号的平均不确定度。

【例2.35】（续例2.32）

计算例2.32给出的二阶马尔可夫信源的熵。

解 式（2.98）已给出该信源全部的一步状态转移概率。再根据各态遍历定理（见式（2.98）），可得下列方程组：

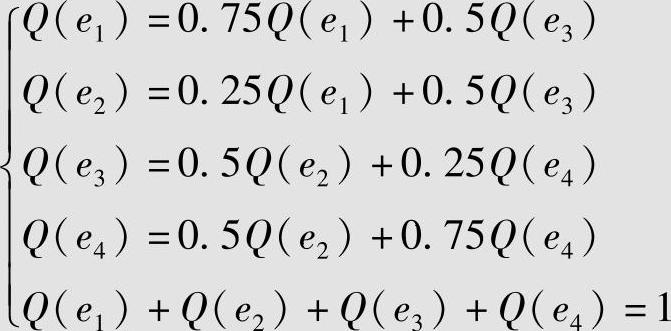
解方程组，求得Q（e₁）=Q（e₄）=1/3，Q（e₂）=Q（e₃）=1/6。代入式（2.102），得信源熵为

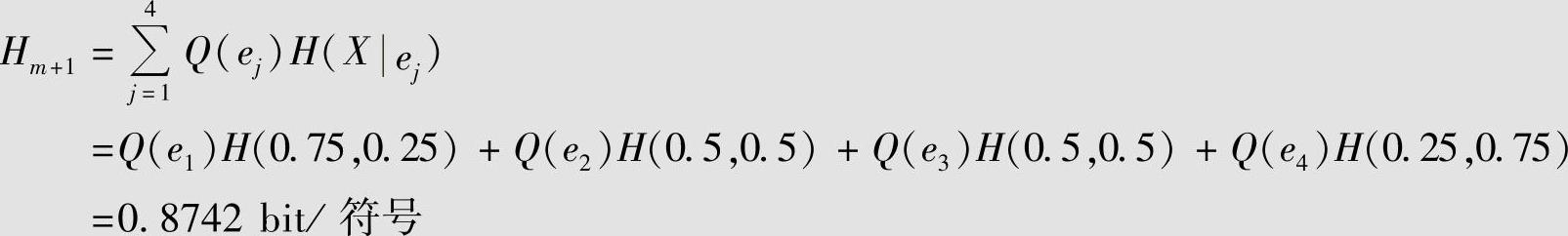
一般的马尔可夫信源并非是平稳的。但当遍历、时齐马尔可夫信源达到稳定后，这时才可以看成是一个平稳信源。由于平稳信源必须知道信源的各维概率分布，而m阶马尔可夫信源只需要知道前m个符号有关的条件概率，就可以计算出信源的信息熵。所以，一般有限记忆长度的平稳信源可以用m阶马尔可夫信源来近似。