离散有记忆序列信源的熵分析

1.离散平稳信源

通常，实际信源不是简单的无记忆信源。因此，无记忆信源的理论适用范围是有限的。实际信源的输出往往是空间或时间的离散随机序列，而且序列中的符号之间有记忆关系。

一般情况下离散信源X的输出序列为X₁，X₂，…，X_i，…。其中，第i时刻信源序列的分量X_i（i=1，2，…）是随机变量，并输出随机事件x_i；X_i的值域是A：{a₁，a₂，…，a_r}。根据离散信源X的概率分布函数满足的条件，给出如下平稳信源的定义：

定义2.16 1）若离散信源X的一维概率分布与时间推移无关，即满足

P（x₁）=P_i（x_i）=P_j（x_j），i，j=2，3，…且i≠j（2.69）

则称信源X是离散一维平稳信源（或一维平稳信源）。

2）若离散信源X的二维联合概率分布与时间推移无关，即满足

P（x₁x₂）=P_i（x_ix_i+1）=P_j（x_jx_j+1），i，j=2，3，…且i≠j（2.70）

则称信源X是离散二维平稳信源（或二维平稳信源）。

3）若离散信源X的k（k≥2）维联合概率分布与时间推移无关，即满足

P（x₁x₂…x_k）=P_i（x_ix_i+1…x_i+k-1）=P_j（x_jx_j+1…x_i+k-1），i，j=2，3，…且i≠j（2.71）

则称信源X是离散k维平稳信源（或k维平稳信源）。

4）若离散信源X的各维联合概率分布均与时间推移无关，即满足

P（x₁x₂…x_N+1）=P_i（x_ix_i+1…x_i+N）=P_j（x_jx_j+1…x_j+N），i≠j且N=1，2，…（2.72）

则称信源X是离散完全平稳信源（或完全平稳信源）。

需要说明的是，k维平稳信源的定义中k是某一确定值，如二维平稳信源就是k=2的k维平稳信源。而在完全平稳信源中，需要对所有的N值都要满足式（2.72）。

根据概率的边缘分布公式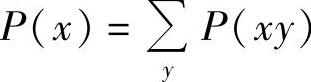，由式（2.71）可以证明下式成立：

P（x₁x₂…x_k-1）=P_i（x_ix_i+1…x_i+k-2）=P_j（x_jx_j+1…x_i+k-2）

上式说明，若信源X是k维平稳信源，则该信源一定是k-1维平稳信源。

因为联合概率与条件概率有下列关系：

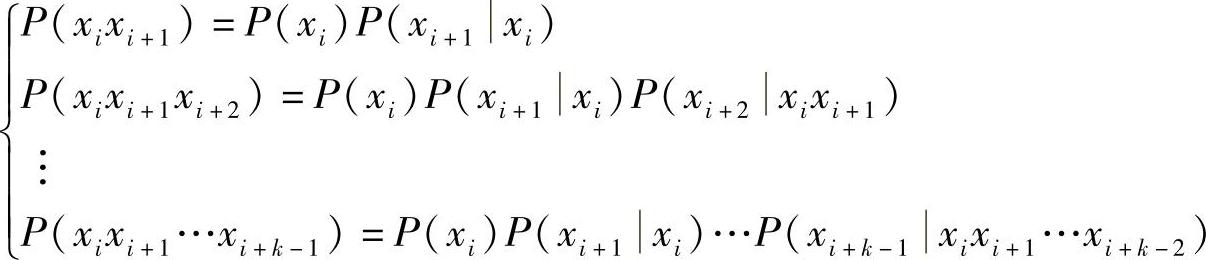
根据k维平稳信源的定义，可得

所以，k维平稳信源的k-1阶条件概率均与时间推移无关，只与关联长度k有关。

2.二维平稳信源的熵

设离散二维平稳信源X的概率空间为

该信源的连续两个信源符号出现的联合概率分布为P（a_ia_j）（i，j=1，2，…，r），并有

根据概率关系可以求得已知a_i符号出现后，跟着a_j符号出现的条件概率为

可见，信源输出的符号序列中相邻两个符号是有关联的。

因为离散二维平稳信源输出的符号序列中相邻两个符号是有记忆的，即只与前一个符号有关联，而且记忆关系不随时间推移而变化。那么就可以把这个二维平稳信源输出的随机序列分成每两个符号一组，每组代表新信源X=X₁X₂中的一个消息，并假设组与组之间是统计独立的（实际上前一组最后一个符号与后一组第一个符号有关联）。这时就可以等效成一个新的离散无记忆信源X₁X₂，该信源的联合概率空间为

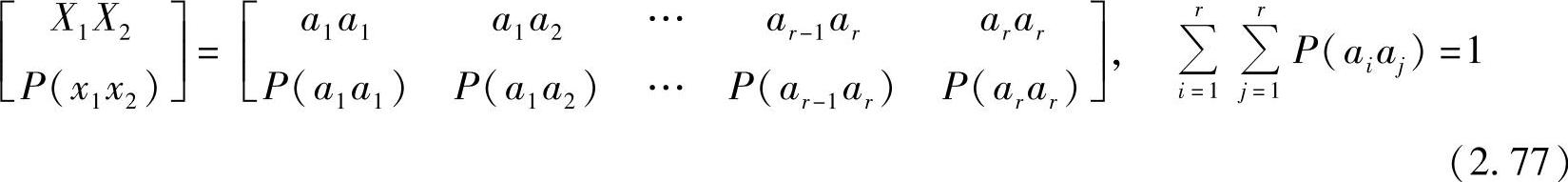
信源X=X₁X₂的熵为

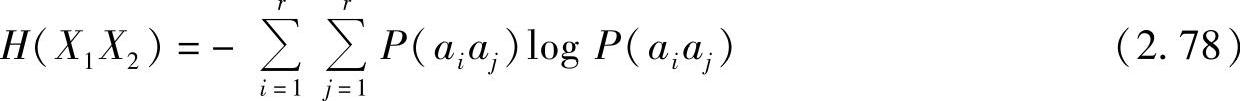
式（2.78）是信源X=X₁X₂输出任意一对消息的共熵。

为此，可以用平均符号熵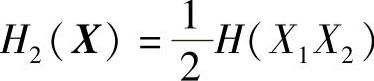（见定义式（2.66））作为离散二维平稳信源X的信息熵的近似值。根据熵的性质和信源特性，可得

由式（2.79）可以推得H（X）≥H₂（X）。这说明，离散无记忆信源的平均不确定度H（X）大于离散有记忆信源的平均不确定度H₂（X）。

再由式（2.79），还可以推得离散二维平稳信源X的条件熵H（X₂X₁）、平均符号熵H₂（X）和无记忆信源熵H（X）三者之间的关系为

式（2.80）说明了有记忆的离散二维平稳信源的联合熵、条件熵、平均符号熵与无记忆信源熵之间的定量关系，这是有关平稳信源的非常重要的结论。

【例2.30】

离散二维平稳信源X的联合概率分布P（a_ia_j）见表2.5。

计算该离散二维平稳信源的无记忆信源熵、条件熵、联合熵和平均符号熵，并验证这些熵之间的关系。

解利用下面两个公式：

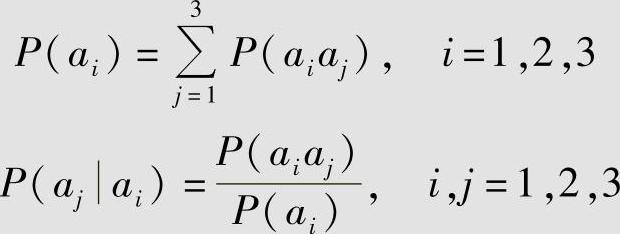
计算该信源的一维概率P（a_i）和条件概率P（a_ja_i），结果列于表2.6和表2.7。当认为信源符号之间无记忆关系时，计算得信源X的信息熵为

表2.5 例2.30信源的联合概率

表2.6 例2.30信源的一维概率

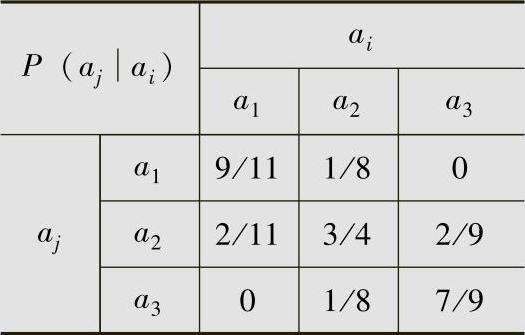
表2.7 例2.30信源的条件概率

(www.xing528.com)

当考虑符号之间有记忆关系时，计算得条件熵为

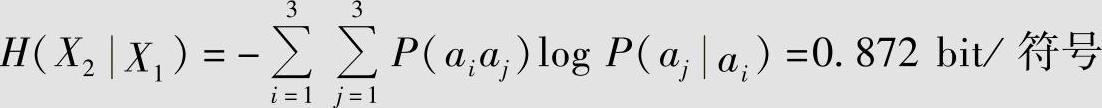
可见，信源的条件熵H（X₂|X₁）比信源无记忆时的熵H（X）减少了0.670bit，这正是因为符号之间有记忆性所造成的。而联合熵为

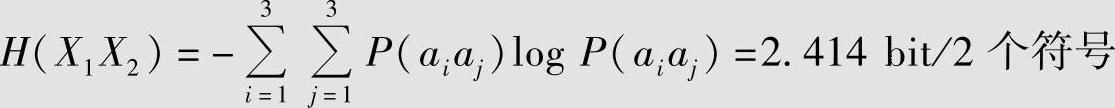
平均符号熵为

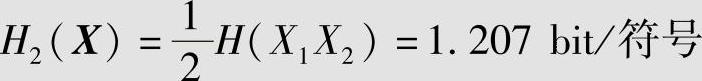
可见，各种熵之间满足H（X₂|X₁）≤H₂（X）≤H（X）。

3.平稳信源的极限熵

对于一般的离散平稳信源X，输出符号之间的相互记忆关系不仅存在于相邻两个符号之间，而且存在于更多（N＞2）个符号之间。

若将信源看成是N维序列信源X=（X₁，X₂，…，X_N）（N=2，3，…），其联合熵H（X）=H（X^N）由式（2.65）所定义，并可以用平均符号熵（N=2，3，…）来近似

表示该信源的实际熵。另外，也可以用条件熵

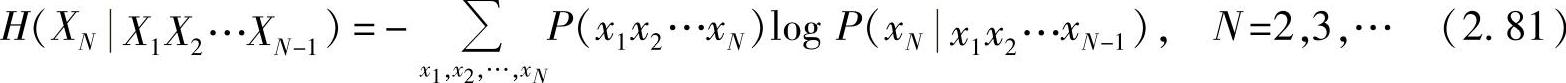
来近似表示该信源的实际熵。

对于一般的离散平稳信源，当H（X）＜∞时，这两种近似熵具有下列性质：

性质2.37 条件熵H（X_N|X₁X₂…X_N-1）随N的增加是非递增的。

性质2.38 N给定时，平均符号熵大于等于条件熵，即H_N（X）≥H（X_N|X₁X₂…X_N-1）。

性质2.39 平均符号熵H_N（X）随N的增加是非递增的。

性质2.40 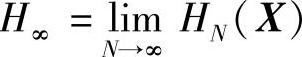存在，并且

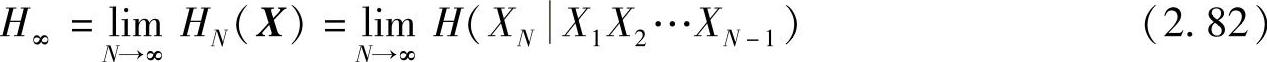
性质2.40表明，H_N（X）和H（X_N|X₁X₂…X_N-1）有相同的极限熵H∞。因此，给出如下定义：

定义2.17 定义H_∞为离散平稳信源的极限熵（或极限信息量、熵率）。

性质2.37表明，在信源输出序列中符号之间前后记忆关系越长，前面若干个符号发出后，其后发生什么符号的平均不确定度就越弱。也就是说，条件较多的熵必小于或等于条件较少的熵，而条件熵必小于等于无条件熵。

性质2.38～性质2.40表明，对于离散平稳信源，当考虑记忆关系为无限长时，平均符号熵和条件熵都非递增地一致趋于平稳信源的信息熵（极限熵）。所以可以用条件熵或者平均符号熵来近似描述信源。

证明（性质2.37～性质2.40）运用熵的性质H（YX）≤H（Y）和平稳信源的平稳特性，有

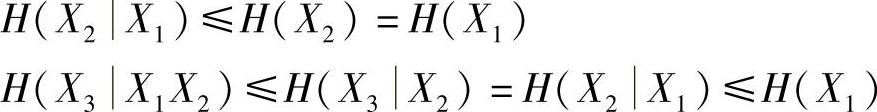
由此递推，对于平稳信源有

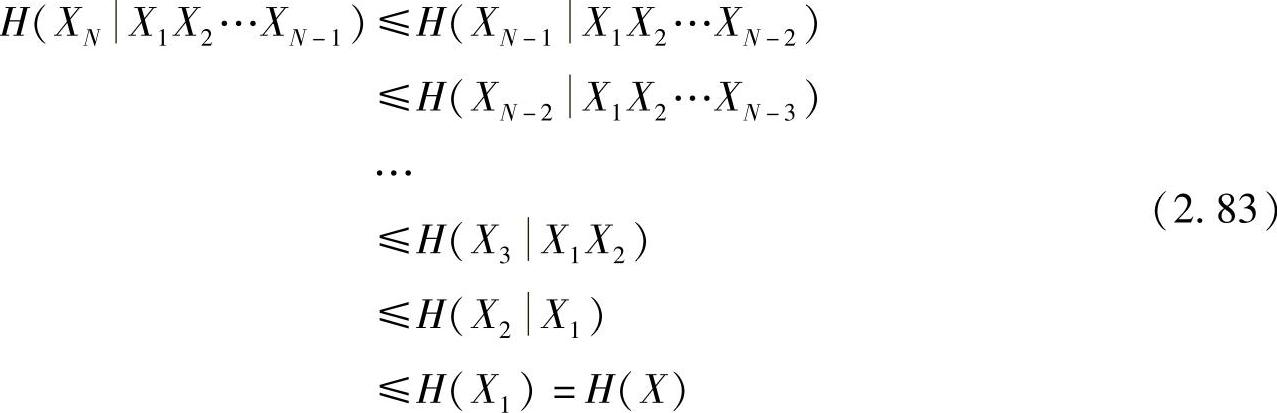
证得性质2.37。

由熵的强可加性（式（2.39）），可知

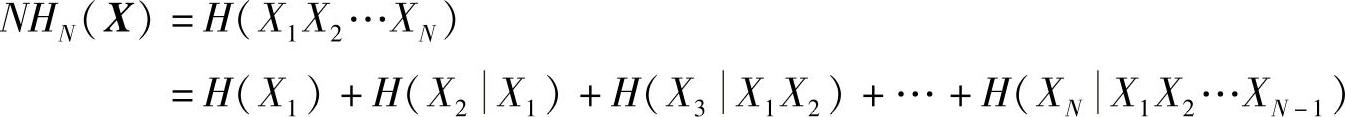
直接运用条件熵的非递增性（性质2.37），得

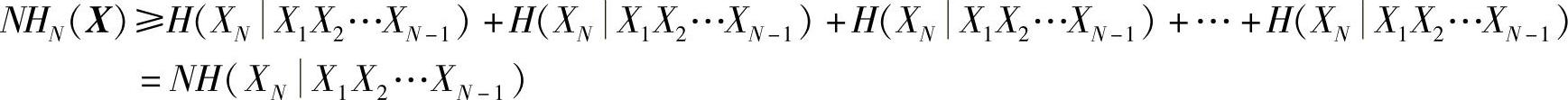
所以，证得性质2.38，即

H_N（X）≥H（X_N|X₁X₂…X_N-1） （2.84）

同理，由熵的强可加性（性质2.17），得

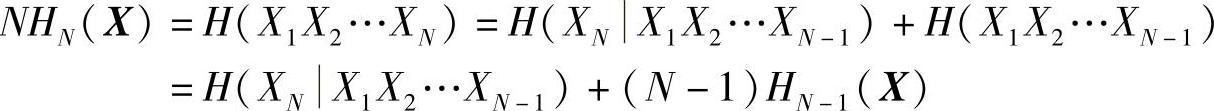
再利用性质2.38，得

NH_N（X）≤H_N（X）+（N-1）H_N-1（X）

所以，有H_N（X）≤H_N-1（X），即H_N（X）随N的增加是非递增的。证得性质2.39。

又因为H_N（X）≥0，即有0≤H_N（X）≤H_N-1（X）≤…≤H₁（X）=H（X）＜∞，故H∞=存在，且处于零和H（X）之间的某一有限值。

另设一整数k，由熵的强可加性（式（2.39）），有

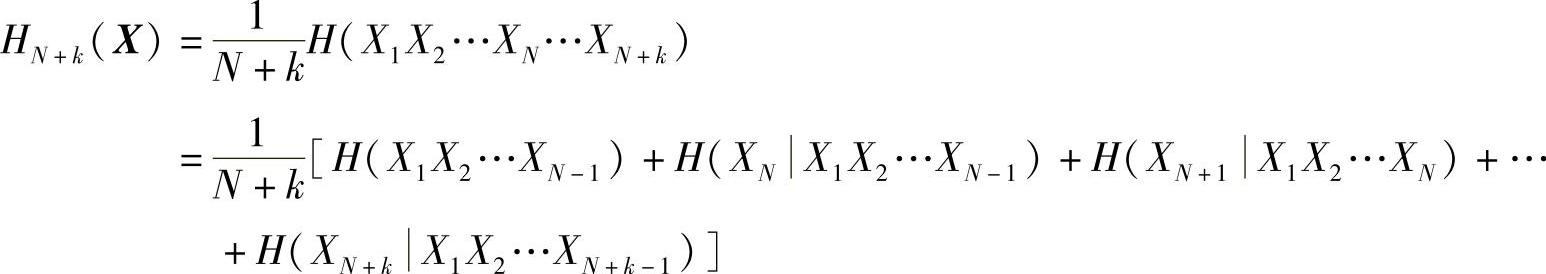
根据条件熵的非递增性（性质2.37）和信源平稳性，有

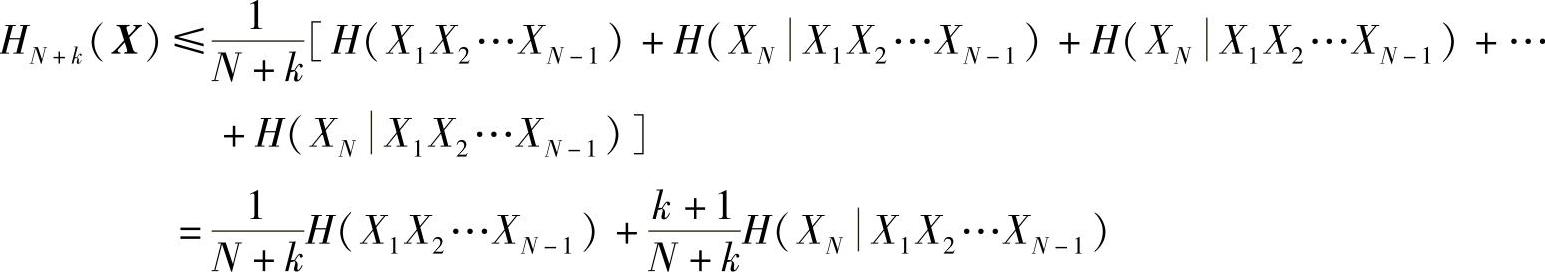
当k足够大（k→∞）时，有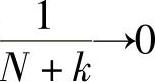和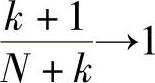。且N是固定的，此时H（X₁X₂…X_N-1）和H（X_N|X₁X₂…X_N-1）为定值，因此，由上式可以推导出

再令上式中的N→∞，因极限存在，所以得

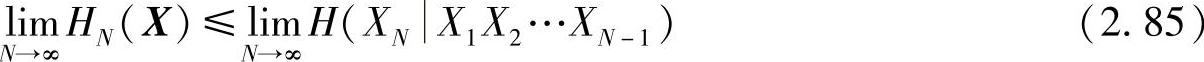
由性质2.38（见式（2.84）），令N→∞得

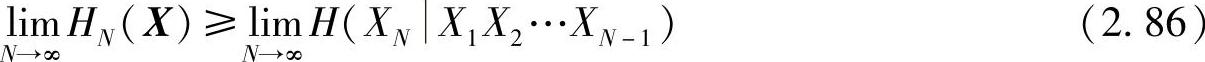
最后，由式（2.85）和式（2.86）得性质2.40成立，即

【证毕】

一般的离散平稳信源实际上就是原始信源在不断地发出符号，符号之间的统计关联关系也并不限于长度N之内，而是伸向无穷远。所以要研究实际信源，必须求出信源的极限熵H∞，才能确切地表达平稳的离散有记忆序列信源平均每发出一个符号所提供的信息量。

要准确地计算出极限熵值H_∞，就必须测定信源的无穷阶联合概率分布或条件概率分布，这是相当困难的。有时为了简化分析，往往用条件熵H（X_N|X₁X₂…X_N-1）或平均符号熵H_N（X）作为极限熵H_∞的近似值。通常即使N值并不很大，这些熵也很接近于H_∞。实践中常使用条件熵H（X_N|X₁X₂…X_N-1）来估算H∞，这是因为计算条件熵更容易一些。