平均互信息的性质解析

性质2.31（非负性）I（X；y=b_j）和I（X；Y）是非负的，即

且当X和Y统计独立时，等式成立。

证明 根据式（2.52），直接应用不等式lnx≤x-1（x＞0）得

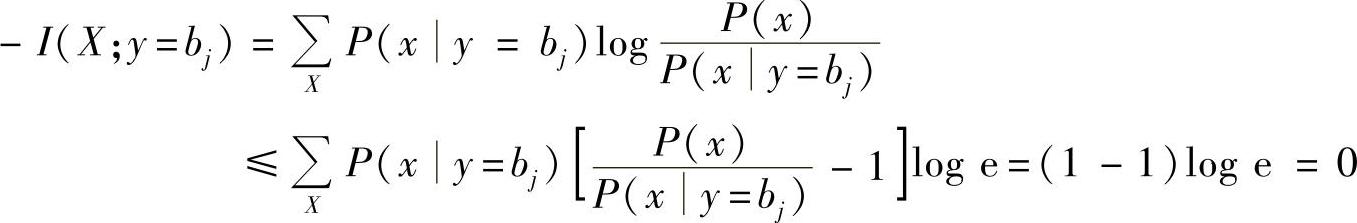
所以，I（X；y=b_j）≥0。而由式（2.54）得

I（X；Y）=E_Y[I（X；y=b_j）]≥0

因为，仅当x=1时，lnx≤x-1的等式成立。所以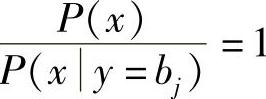，即P（x）=P（x|y=b_j）时，式（2.60）和式（2.61）的等式成立。而P（x）=P（x|y=b_j）说明，X和Y统计独立。

【证毕】

平均互信息的非负性表明，从整体和平均的意义上来说，信源消息通过信道传输到收信端后，收信者总能从收到的消息中获取到信源的信息量，等效于总能使信源的不确定度有所下降。也可以说，从一个事件提取关于另一个事件的平均信息，在最坏情况下是信息量为零，不会由于知道了一个事件，反而使另一个事件的不确定度增加。

如果从人们学习的角度来看互信息，则说明当经过一段时间的学习后，人们的知识量和文化修养总会有所提高。

性质2.32（极值性） 平均互信息I（X；Y）分别小于等于X和Y的熵，即

I（X；Y）≤H（X） （2.62）

I（X；Y）≤H（Y） （2.63）

证明 因为I（X；Y）=H（X）-H（X|Y），而条件熵H（X|Y）为非负，故式（2.62）成立。同理，式（2.63）也成立。

【证毕】

性质2.33（互易性、对称性）I（X；Y）=I（Y；X）。

证明 将式（2.55）中的变量X和Y互换，得I（Y；X）=H（Y）-H（Y|X），再与式（2.56）比较，可得I（X；Y）=I（Y；X）。

【证毕】

将式（2.55）和式（2.56）重写如下：

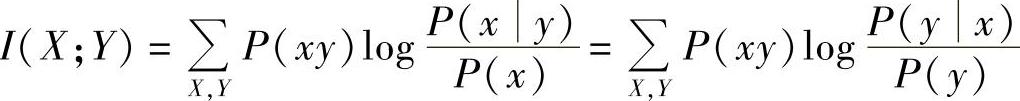
结合等式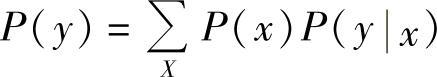可见，平均互信息I（X；Y）是输入信源X的概率分布P（x）和信道转移概率P（y|x）的函数，即I（X；Y）=I[P（x），P（y|x）]。平均互信息只与信源概率分布和信道转移概率有关，因此对于不同信源和不同信道得到的平均互信息是不同的。为此，可以得到有关平均互信息凸性质如下：

性质2.34（上凸性） 平均互信息I（X；Y）是输入信源概率分布P（x）的∩形函数（又称上凸函数）。

性质2.35（下凸性） 平均互信息I（X；Y）是信道转移概率分布P（y|x）的∪形函数（又称下凸函数）。

证明 先证明性质2.34，根据∩形函数的定义来进行证明。(www.xing528.com)

先固定信道，即固定信道转移概率P（y|x），则I（X；Y）仅是信源概率分布P（x）的函数，简写为I[P（x）]。设信源的两种概率分布为P₁（x）、P₂（x），对应的平均互信息分别为I[P₁（x）]和I[P₂（x）]。取，令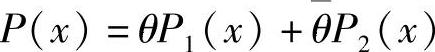，可知P（x）满足概率分布条件，对应P（x）的平均互信息记为I[P（x）]。现要证明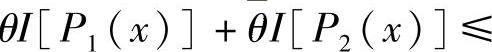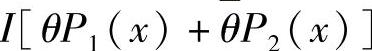。计算

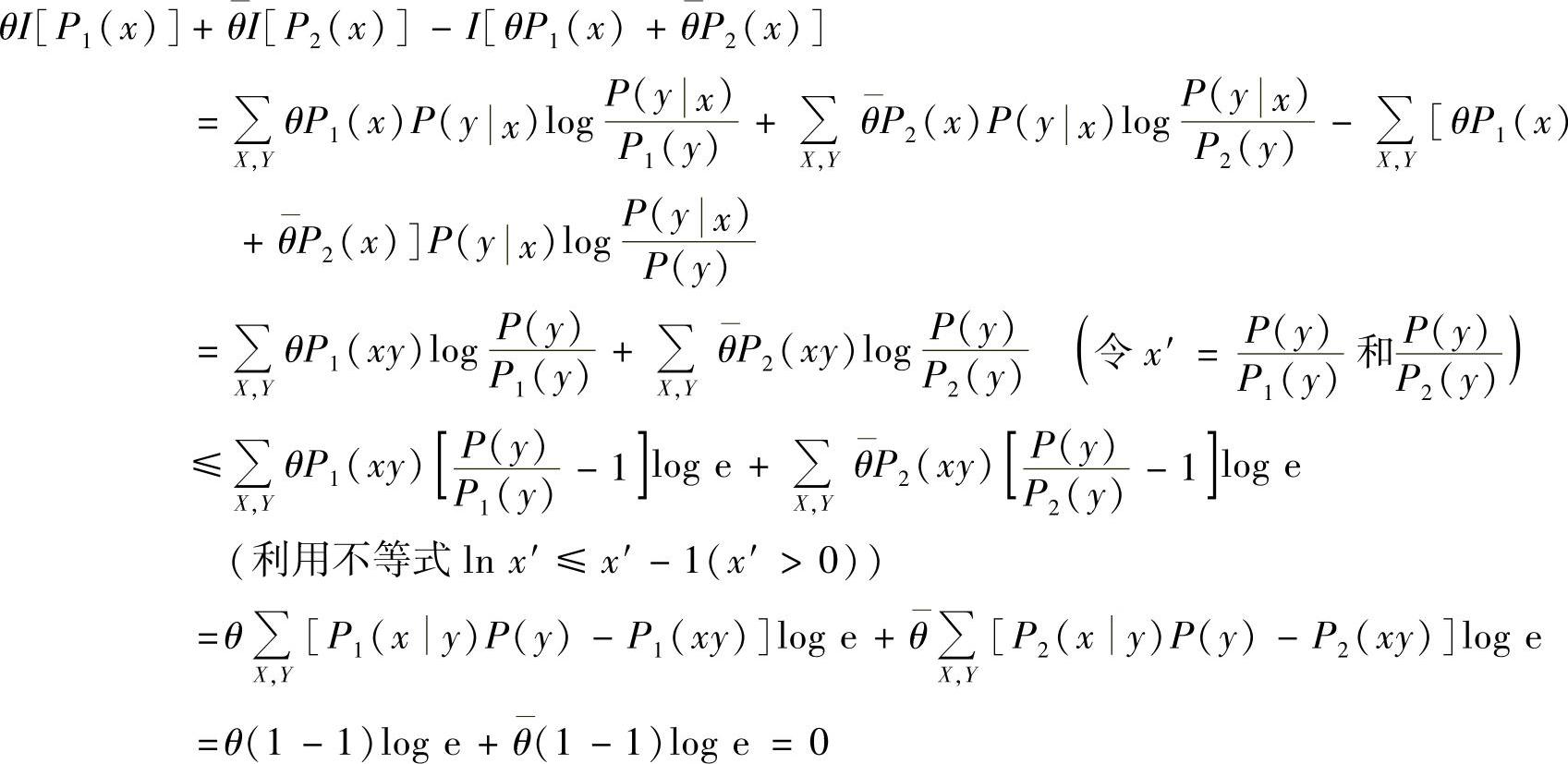
即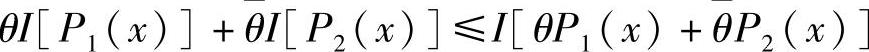，因此I（X；Y）是信源概率分布P（x）的∩形函数（又称上凸函数）。

再证明性质2.35，根据∪形函数的定义来进行证明。

先固定信源，即固定信源概率P（x），则I（X；Y）仅是信道转移概率P（y|x）的函数，简写为I[P（y|x）]。设信道的两种概率分布为P₁（y|x）、P₂（y|x），对应的平均互信息分别为I[P₁（y|x）]和I[P₂（y|x）]。取0＜θ＜1和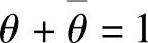，令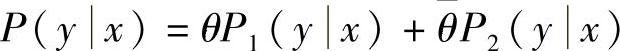，可知P（y|x）满足概率分布条件，对应P（y|x）的平均互信息为I[P（y|x）]。现要证明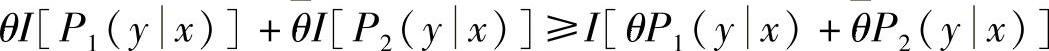。计算

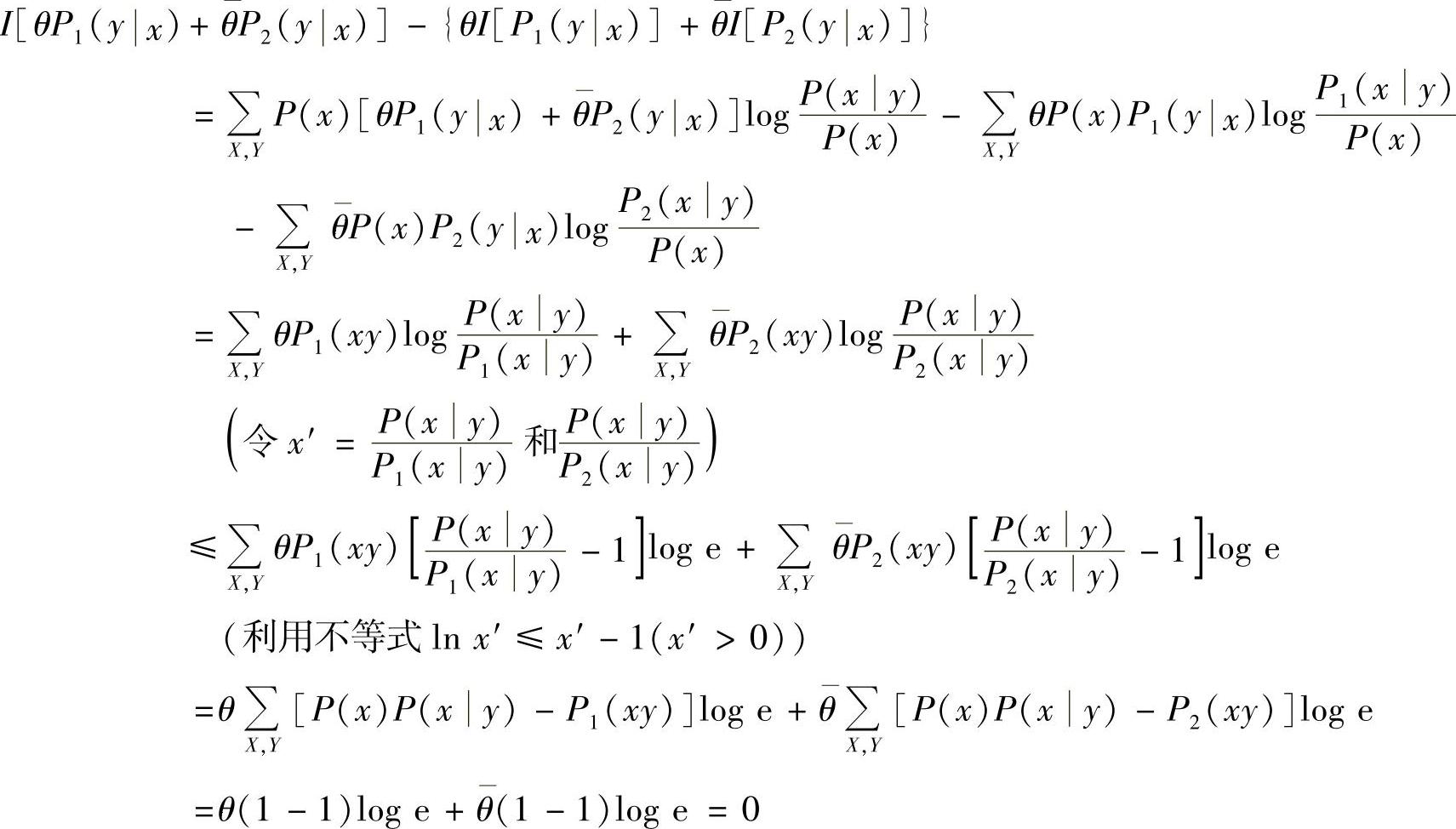
即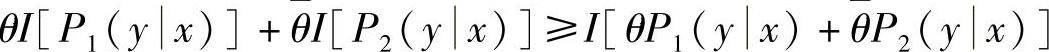，因此I（X；Y）是信道转移概率分布P（y\x）的∪形函数（又称下凸函数）。

【证毕】

【例2.27】

二元离散随机变量X和Y的值域相同（皆为A：{0，1}）。设X的概率分布为P（x=0）=ω和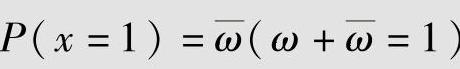，X和Y之间的条件概率为P（y=0|x=0）=P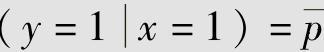和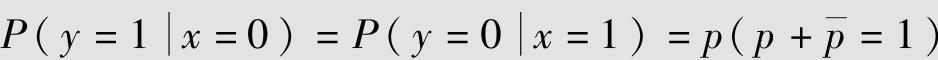。计算Y的概率分布为

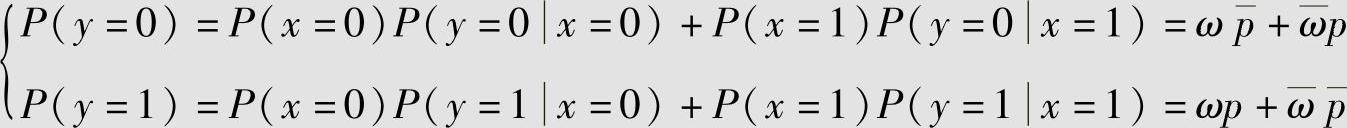
计算平均互信息I（X；Y）为

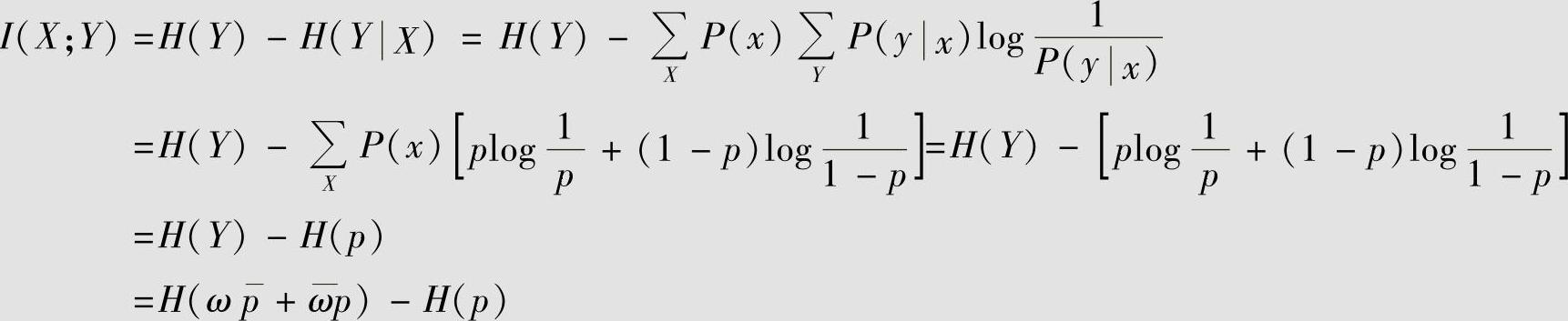
可见，I（X；Y）是信源X的概率ω和条件概率p的函数。固定条件概率p，I（X；Y）与信源X的概率ω的函数关系如图2.4a所示，这是一个上凸函数，当ω=1/2时（等概率分布时），I（X；Y）取最大值I（X；Y）=1-H（p）。固定信源X的概率ω，I（X；Y）与条件概率p的函数关系如图2.4b所示，这是一个下凸函数，当p=1/2时，I（X；Y）取最小值I（X；Y）=0。

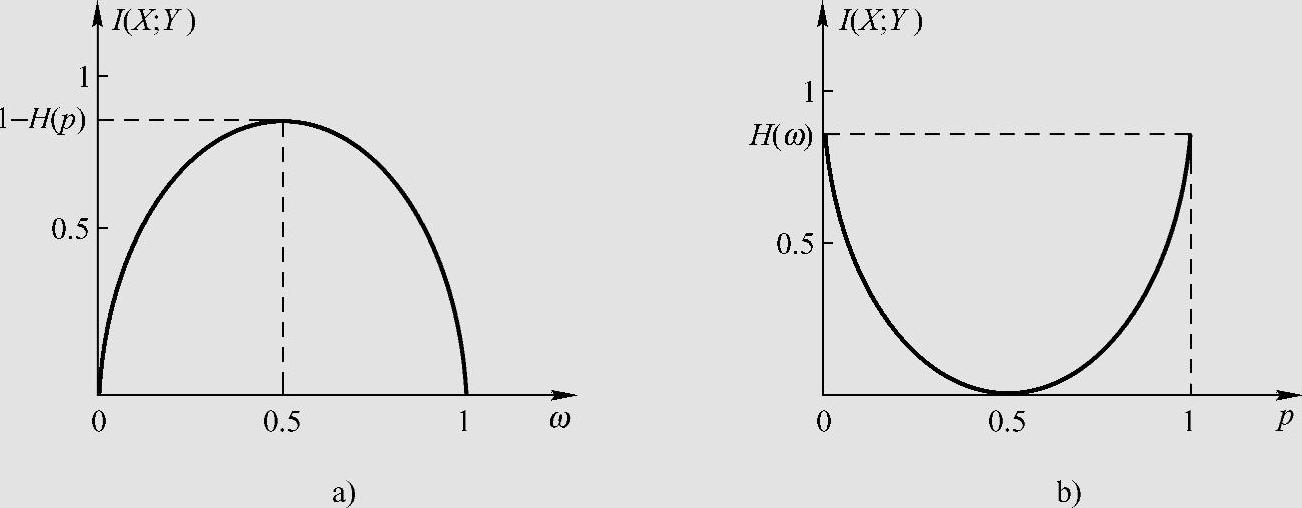
图2.4 二元信源的熵函数

a）I（X；Y）与ω的函数关系 b）I（X；Y）与p的函数关系

如果把条件概率P（y|x）视为信道的转移概率，则性质2.35说明，当信道固定时存在一种最佳信源输入分布P（x），使输出端获得的平均信息量最大。

性质2.36 在三维离散联合随机变量集XYZ上，平均互信息、平均联合互信息和平均条件互信息有下列关系：

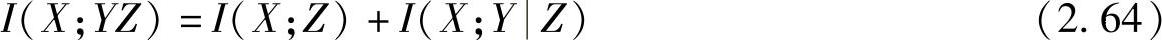
证明 由平均联合互信息的定义得

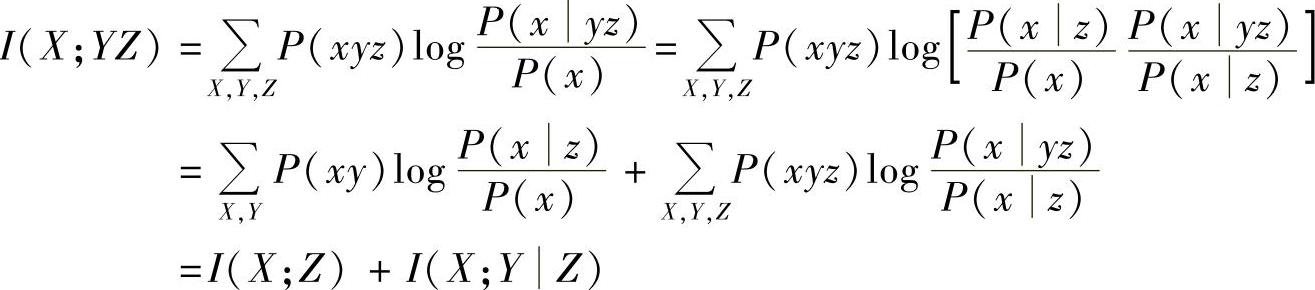
【证毕】