加权熵：概念及基本性质

Shannon定义的信息量和熵并没有考虑人的主观因素，只是信息系统概率的函数，是“客观信息”。在实际中，各种事件虽以一定的概率发生，但各种事件的发生对不同的人有不同的意义，其重要性也因人而异。在许多场合，通常很难忽略与个人目的有关的主观因素。如高考分数线的划定，对当年参加高考的考生来说至关重要，也是考生家长十分关心的问题，但是对于其他人来说并无多大意义。

为了把主观价值和主观意义反映出来，可以引入加权熵的概念。

设信源（随机变量）X的概率空间为

式中，概率P（a₁），P（a₂），…，P（a_r）也可以简记为p₁，p₂，…，p_r。

对消息a_i（i=1，2，…，r）确定一个非负的实数w_i（i=1，2，…，r）作为消息a_i的“重量”，就如同物理学中常见的加权一样。因此，w_i也可以看成是消息a_i的“效用权重系数”。把消息a_i的重量w_i与消息的重要性和意义联系起来，如果一个消息a_i比另一个消息a_j更有意义，或更有效用，那么消息a_i的重量w_i就应比消息a_j的重量w_j更大，即w_i＞w_j。于是，对上述信源构造一个相应的重量空间为

定义2.10 信息的加权熵定义为消息a_i的重量w_i对自信息I（a_i）的加权平均值，即

可见，加权熵的大小不仅与随机事件发生的客观概率有关，也依赖于消息的主观重量。“重量”与“概率”之间没有简单明了的关系。一个概率很小的事件或许具有很大的意义，也可能没有什么价值。例如，“冬天下大雪”这种自然现象在东北地区司空见惯，对东北人来说并无特殊意义，但是同样的自然现象如果发生在南方则是非常稀罕的事，人们会感到非常兴奋，会纷纷走出家门观赏雪景。显然，“冬天下大雪”在南方发生的概率很小，但是对人们的意义很大。

可见，把自信息按照主观因素加权后，对不同的人可以得到不同的意义信息，引入加权熵的概念后，实际上从某种程度上反映了人的主观因素。

加权熵具有一系列性质，下面先给出与Shannon熵类似的加权熵性质。

性质2.20（非负性）H_w（X）=H_w（w₁，w₂，…，w_r；p₁，p₂，…，p_r）≥0。

加权熵的非负性表明，在赋予事件的效用后，信源的事件发生后总能提供一定的平均信息量，至少等于零。这一点与信息熵的非负性相同。

性质2.21（对称性） 当变量w₁，w₂，…，w_r和p₁，p₂，…，p_r的顺序以相同方式任意互换时，加权熵不变，即

加权熵是对信源的自信息用信源消息的概率和重量进行加权后再求和的结果。信源消息的概率及其相应重量的顺序互换时，只是求和的顺序不同，并不影响求和的结果。加权熵的对称性说明它的值只取决于信源的概率空间及其相应的重量空间的总体结构，与信源的具体消息无关。这是熵的总体特性的再度体现。

性质2.22（确定性） 信源中有一个事件必然出现，其他事件不可能出现时，其加权熵为0。

加权熵的确定性表明，只包含一个实验结果的事件是确定事件，没有任何随机性，尽管发生的事件是有效用或有意义的，仍然不能提供任何信息量。这个结论与Shannon熵是一致的。

性质2.23（扩展性） 在信源概率空间中增加一个基本不会出现的小概率事件，其加权熵不变，即

加权熵的扩展性表明，增加一个有效用或意义很大但是不可能发生的消息，其信源的加权熵值不变。这也是熵的总体平均性的体现。

性质2.24（连续性） 信源概率空间中概率分量的微小波动不会引起加权熵的变化，即

加权熵的连续性表明，信源空间中概率分量的微小波动，不会引起加权熵值的很大变动。这仍是熵的总体平均性的体现。(www.xing528.com)

性质2.25（递增性）

式中，p_r=p′+p″，。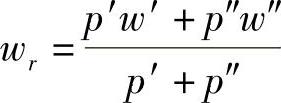

加权熵的递增性表明，信源发生分割或分裂时，加权熵也增加。增加量与分割出新事件的发生概率及新事件的效用或意义的大小有关。若信源事件（包括分割出的新事件）的权重都相等，则加权熵的递增性就退化成Shannon熵的递增性。

性质2.20～性质2.25的证明方法与Shannon熵相对应的性质的证明方法类似，这些性质的证明留作习题。

除了上述与Shannon熵相近的加权熵的性质外，由于加权的特殊性，也产生了一些加权熵特有的性质。这些性质如下：

性质2.26（等重性） 设各事件的权重都相等，即w₁=w₂=…=w_r=w，则加权熵为

H_w（w，w，…，w；p₁，p₂，…，p_r）=wH（p₁，p₂，…，p_r）（2.49）

式（2.49）说明，权重系数均为w的等重信源，其加权熵是信源熵的w倍。

性质2.27（均匀性） 设信源X是具有r个消息的等概信源，则加权熵为

加权熵的均匀性表明，等概信源的加权熵等于离散信源的最大熵与r个权重系数的算术平均值的乘积。

性质2.28（无重性） 设各事件的权重都等于零，即w₁=w₂=…=w_r=0，则加权熵为零。

加权熵的无重性表明，当信源所有可能发生的事件都是无意义或无效用时，尽管Shan_- non熵不等于零，但获得的都是无用的、无意义的信息，从效用性或意义性角度观察，所获得的信息应等于零，所以加权熵等于零。

性质2.29（非容性） 若事件的概率和效用满足两个条件之一，即当w_i≠0时p_i=0，或者当w_i=0时p_i≠0，则加权熵为零。

加权熵的非容性表明，如果可能的事件是无意义的或无效用的，而有意义的或有效用的事件是不可能的，尽管Shannon熵不为零，但其提供的加权熵等于零。

性质2.30（线性叠加性） 对于非负实数λ，有

加权熵的线性叠加性表明，当某一信源发出的每一种不同消息的效用或意义同时扩大若干倍时，其加权熵也扩大同样的倍数。

由加权熵的定义式可以很容易地证明性质2.26～性质2.30，这些性质的证明留作习题。

以上引入的加权熵虽然在一定程度上能够反映信息对收信者的主观价值。但是，对于全面解决与人们主观价值和主观意志有关的信息问题来说，显然是不够的。为此，人们不断地对信息的测度提出了新的定义，如语义信息、语用信息、模糊信息和定性信息等，但这些研究还没有获得令人满意的统一结果。