熵函数性质分析

由式（2.23）知，信息熵H（X）是随机变量X的概率分布P=（p₁，p₂，…，p_r）的函数，即H（X）=H（P）=H（p₁，p₂，…，p_r），所以H（X）又称为熵函数。需要指出的是，因为

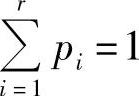，所以H（X）是r-1元函数。

熵函数H（X）具有以下性质：

性质2.8（非负性）对于离散集合X，有

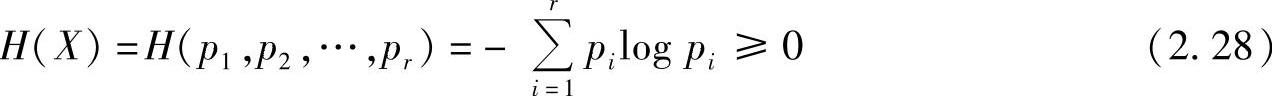
其中，等号成立的充要条件是对某个i，p_i=1，其余的p_k=0（k≠i）。

证明 因为p_i≤1（i=1，2，…，r），所以-p_ilogp_i≥0，于是有式（2.28）成立。

充分性：当概率满足条件，对某个i，p_i=1，其余的p_k=0（k≠i）时，有

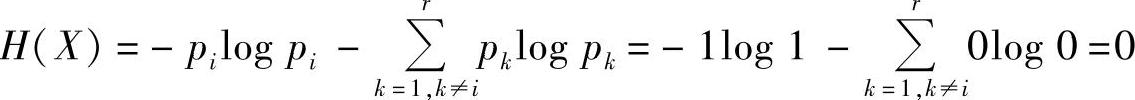
必要性：前面已证明对于任意i=1，2，…，r，均有-p_ilogp_i≥0。因此，若H（X）=0，则对于任意i=1，2，…，r，必有-p_ilogp_i=0，即必有p_i=0或者p_i=1。又因为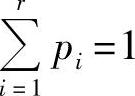，所以，对某个i，p_i=1，其余的p_k=0（k≠i）。

【证毕】

熵函数的非负性说明，当集合中有一个事件必然出现，其他事件不可能出现时，集合的熵为0，此时这个集合没有不确定度；否则这个集合或多或少总会存在一定的不确定度。

性质2.9（对称性）当变量p₁，p₂，…，p_r的顺序任意互换时，熵函数的值不变，即

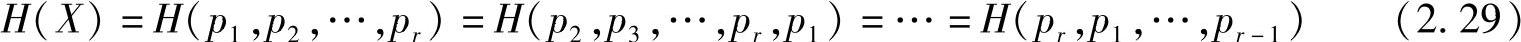
由熵函数的定义式可以直接证明性质2.9。

熵函数的对称性说明信源熵具有局限性，它仅与信源的总体结构（统计特性）有关。如果某些信源的统计特性相同（含有的消息数和概率分布相同），那么这些信源的熵就相同。

【例2.22】

有三个信源，其概率空间分别为

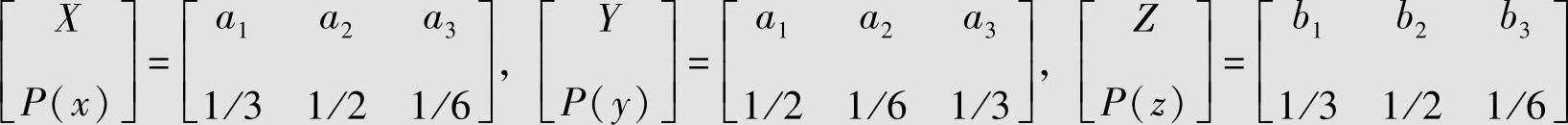
若其中a₁、a₂、a₃分别表示红、黄、蓝三个具体消息，而b₁、b₂、b₃分别表示晴、雾、雨三个消息。在这三个信源中，信源X与Z的差别是它们所选择的具体消息（符号）的含义不同，而信源X与Y的差别是它们选择的某同一消息的概率不同。但它们的信息熵是相同的，即表示这三个信源总的统计特性是相同的，也就是它们的符号数和概率分量的总体结构是相同的，即

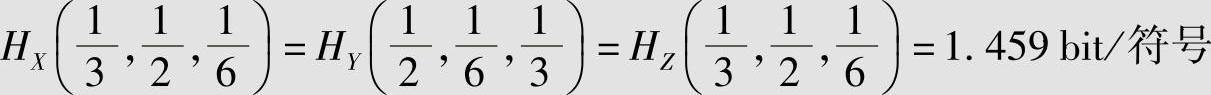
【例2.23】

A、B两地的天气情况分别如表2.2所列。由信息熵的定义式（2.22），A、B两地天气情况的平均不确定度为

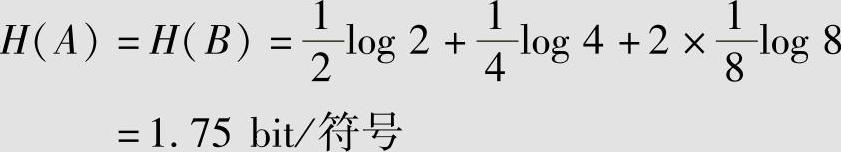
表2.2 例2.23中A和B两地的天气情况

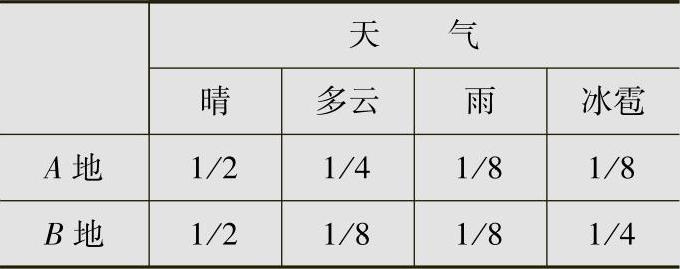
由此看出，A、B两地的信息熵是相同的，但是信息熵未能描述事件本身的具体含义和主观价值。显然，冰雹将导致严重灾害，这一情况未能从信息熵中反映出来，这是十分遗憾的。

从例2.22和例2.23中可以看到，Shannon熵仅表征了信源信息输出的总的统计特征，或总体的平均不确定度。这也说明了所定义的Shannon熵有它的局限性。它不能描述事件本身的具体含义和主观价值等，因此，引出了加权熵的概念（见2.3.5节）。加权熵中对不同的元素分别给予不同权重，从而可以反映不同事件的主观价值。

性质2.10 （确定性）信源中有一个事件必然出现，其他事件不可能出现时，其熵为0。

由熵函数的非负性（性质2.8）的证明可以直接证明该性质。

熵函数的确定性意味着从总体来看，信源虽然有不同的输出符号，但它只有一个符号几乎必然出现，而其他符号几乎不可能出现，那么该信源就是一个确定信源，其信源熵等于零。

性质2.11 （扩展性）在信源概率空间中增加一个基本不会出现的小概率事件，其信息熵不变，即

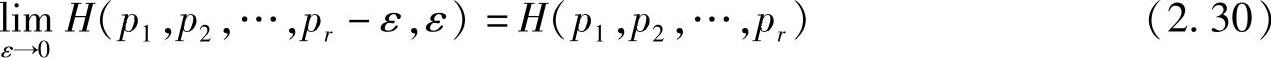
熵函数的扩展性的含义是，虽然小概率事件的出现给予收信者的信息量很大，但在信息熵的计算中，它占的比重很小，可以忽略不计，这也是信息熵的总体平均性的体现。根据熵函数的扩展性，在工程中可以仅对概率相对较大的消息进行处理，而忽略概率极小的事件，这样做并不会引起较大的处理误差。

性质2.12（连续性）在信源概率空间中概率分量的微小波动，不会引起信源熵的变化，即

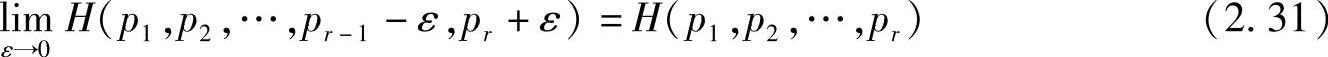
熵函数的连续性表明，信源空间中概率分量的微小波动，不会引起信源熵的很大变动。这仍是信源熵的总体平均性的体现。

性质2.13（递增性）

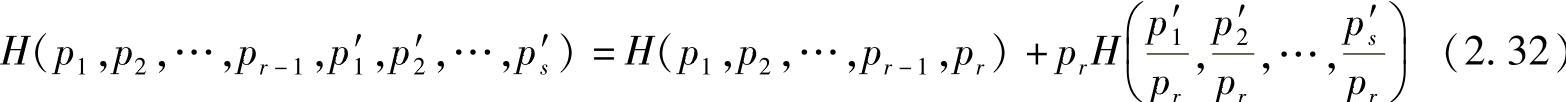
式中，，。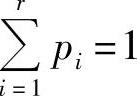

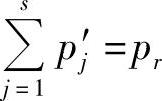可以用信息熵的定义式来证明性质2.13。以上性质2.11～性质2.13的证明作为习题留给读者练习。

熵函数的递增性表明，假如有一信源的r个元素的概率分布为p₁，p₂，…，p_r，其中某个元素a_r又被划分成s个元素，这s个元素的概率之和等于元素a_r的概率，这样得到的新信源的熵中增加了一项，增加的一项是由于划分产生的不确定度。

【例2.24】

利用熵函数的递增性计算H（1/2，1/8，1/8，1/8，1/8）。

解 利用式（2.32），得

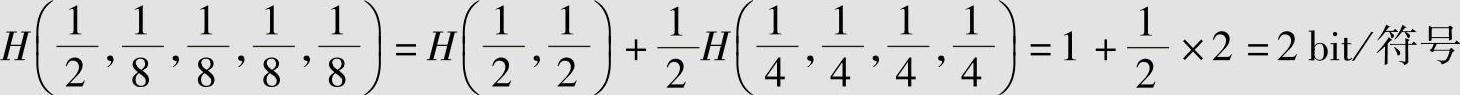
性质2.14（极值性）设信源X有r个消息，则其信源熵H（X）满足不等式

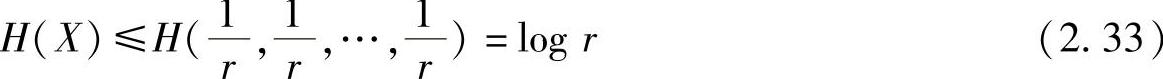
当且仅当X中各消息等概分布时，等号成立。

证明^[2] 利用不等式lnx≤x-1（x＞0；仅当x=1时等式成立），来证明该性质。

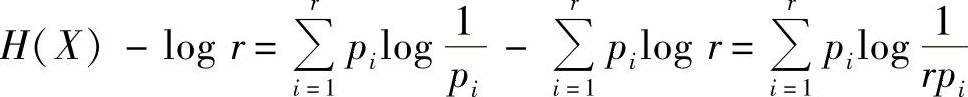
令x=1/（rp_i），利用不等式ln x≤x-1（x＞0），并注意到logx=ln x·log e，得

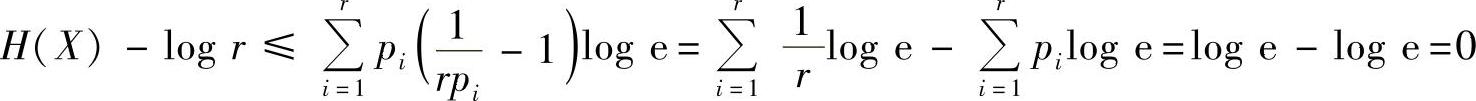
故有H（X）≤logr，当且仅当x=1/（rp_i）=1，即p_i=1/r时，H（X）≤logr中的等号成立。

利用詹森（Jensen）不等式来证明该性质。

由于logx在正实数集（x＞0）上是上凸函数，所以根据Jensen不等式E[logx]≤logE[x]，有(www.xing528.com)

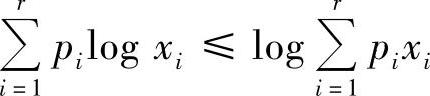
令x_i=1/p_i，代入上式，得

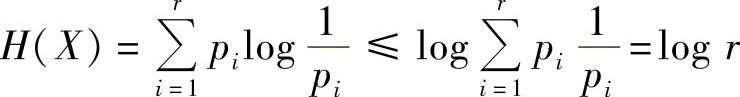
且只有当p_i=1/r时，有。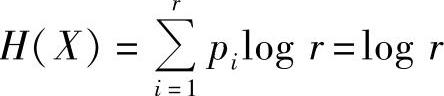

【证毕】

熵函数的极值性表明离散信源中各消息等概率出现时信源熵最大，这就是最大离散熵定理。

性质2.15（上凸性）熵函数H（P）是概率矢量P的严格∩型凸函数（或上凸函数）。即对任意概率矢量P=（p₁，p₂，…，p_r）和P′=（p′₁，p₂′，…，p_r′），及任意0＜θ＜1，有

H[θP+（1-θ）P′]＞θH（P）+（1-θ）H（P′） （2.34）

证明

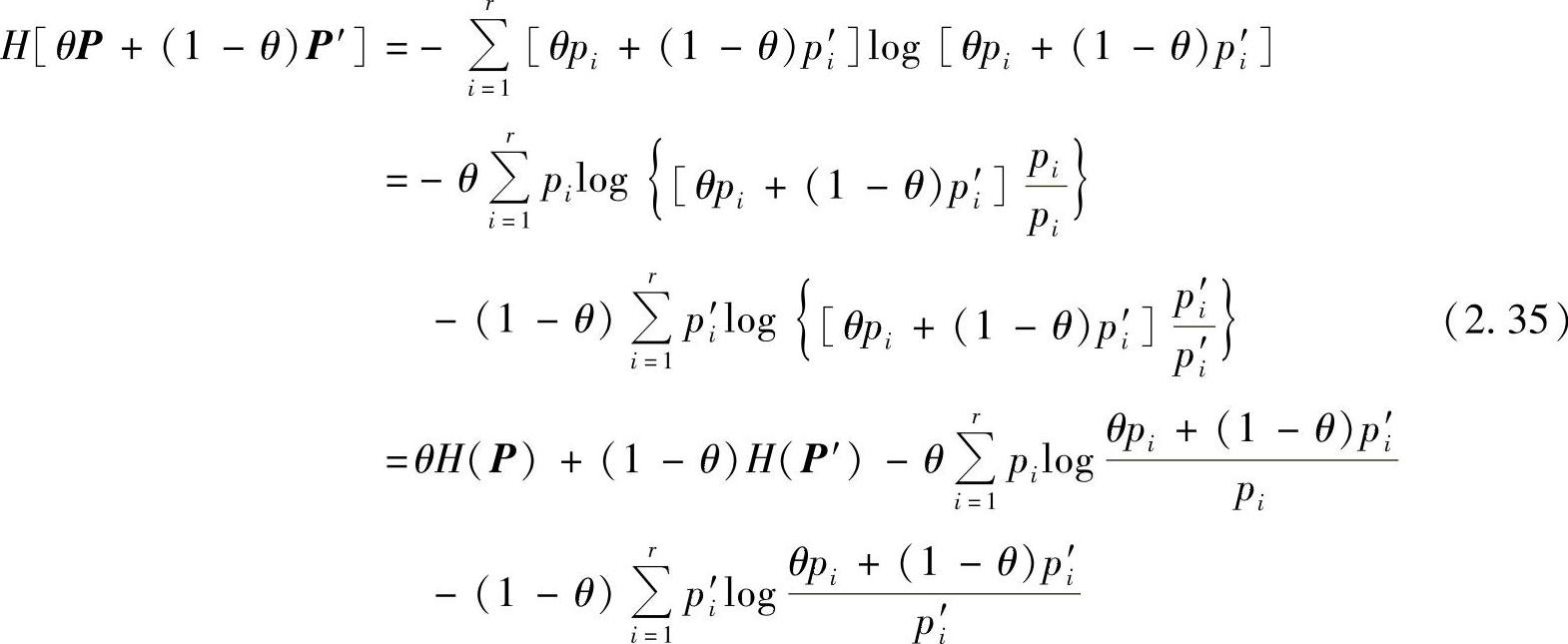
令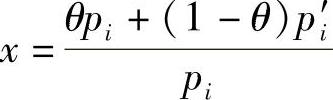，引用不等式ln x≤x-1（x＞0），并注意到log x=ln x·log e，得

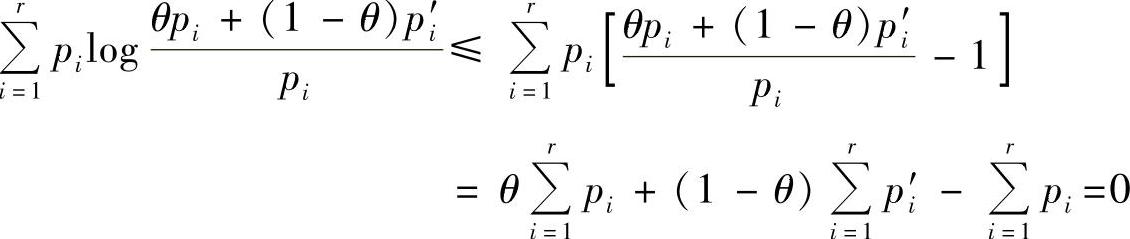
同理可证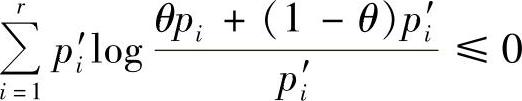，。由于式（2.35）右边后两项的值均大于等于零，因此

H[θP+（1-θ）P′]≥θH（P）+（1-θ）H（P′）

因为ln x≤x-1仅在x=1时等号成立，由此推得上式仅在θ=0和1时等号成立。所以式（2.34）成立。

【证毕】

上凸函数在定义域内的极值必为极大值，可以利用熵函数的上凸性证明熵函数的极值性（性质2.14），请读者自行证明。

【例2.25】

二元信源的符号集为A：{0，1}，概率分布为P（0）=ω，P（1）=1-ω（0≤ω≤1），熵函数为H（ω）=-ωlogω-（1-ω）log（1-ω），图2.3是熵函数的图形表示。可见，当信源输出的消息等概率分布时，P（0）=P（1）=0.5，信源熵达到每信源符号1 bit的最大值。因此，当二元数字是由等概的二元信源输出时，每个二元数字提供1 bit信息量。

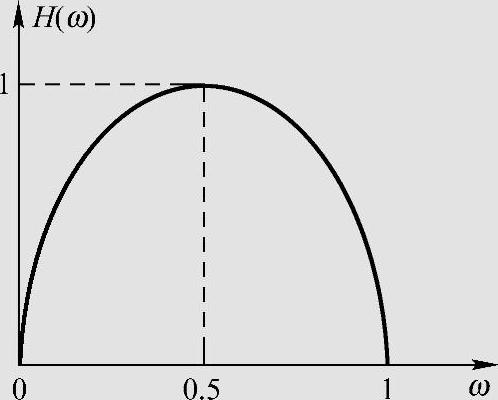
图2.3 二元信源的熵函数

信源熵、联合熵和条件熵之间的关系也是熵函数性质的一部分。

性质2.16（可加性） 两个信源X和Y相互独立时，其联合熵等于X和Y的熵之和，即

H（XY）=H（X）+H（Y）（2.36）

性质2.17（强可加性） 两个互相关联的信源X和Y的联合熵等于信源X（或Y）的熵加上在X（或Y）已知条件下信源Y（或X）的条件熵，即

证明 由联合熵的定义式（2.27），得

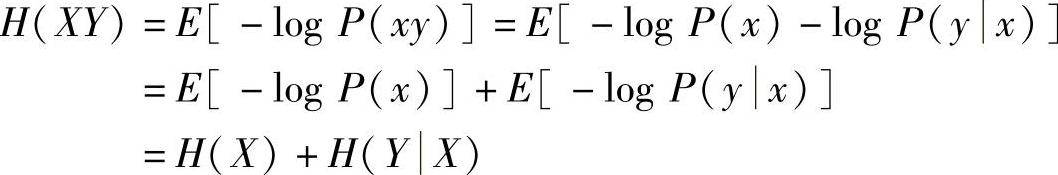
同理可证H（XY）=H（Y）+H（X|Y），因此，式（2.37）的强可加性成立。另当信源X和Y相互独立时，有P（y）=P（y|x），H（Y|X）=E[-logP（y|x）]=E[-logP（y）]=H（Y），把H（Y|X）=H（Y）代入H（XY）=H（X）+H（Y|X）后可得式（2.36）的可加性成立。

【证毕】

性质2.16和性质2.17可以推广到多个信源的情况。当信源X₁，X₂，…，X_N相互独立时，有下列联合熵的可加性：

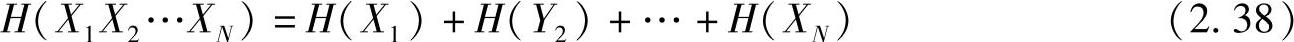
一般地，信源X₁，X₂，…，X_N的联合熵的强可加性为

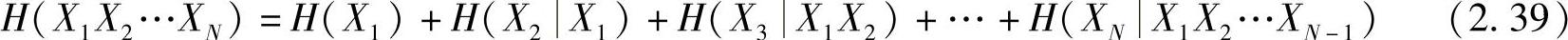
性质2.18（熵的不增原理）在离散联合随机变量集XY上，条件熵总是小于或等于无条件熵，即

证明 利用不等式lnx≤x-1（x＞0）来证明。

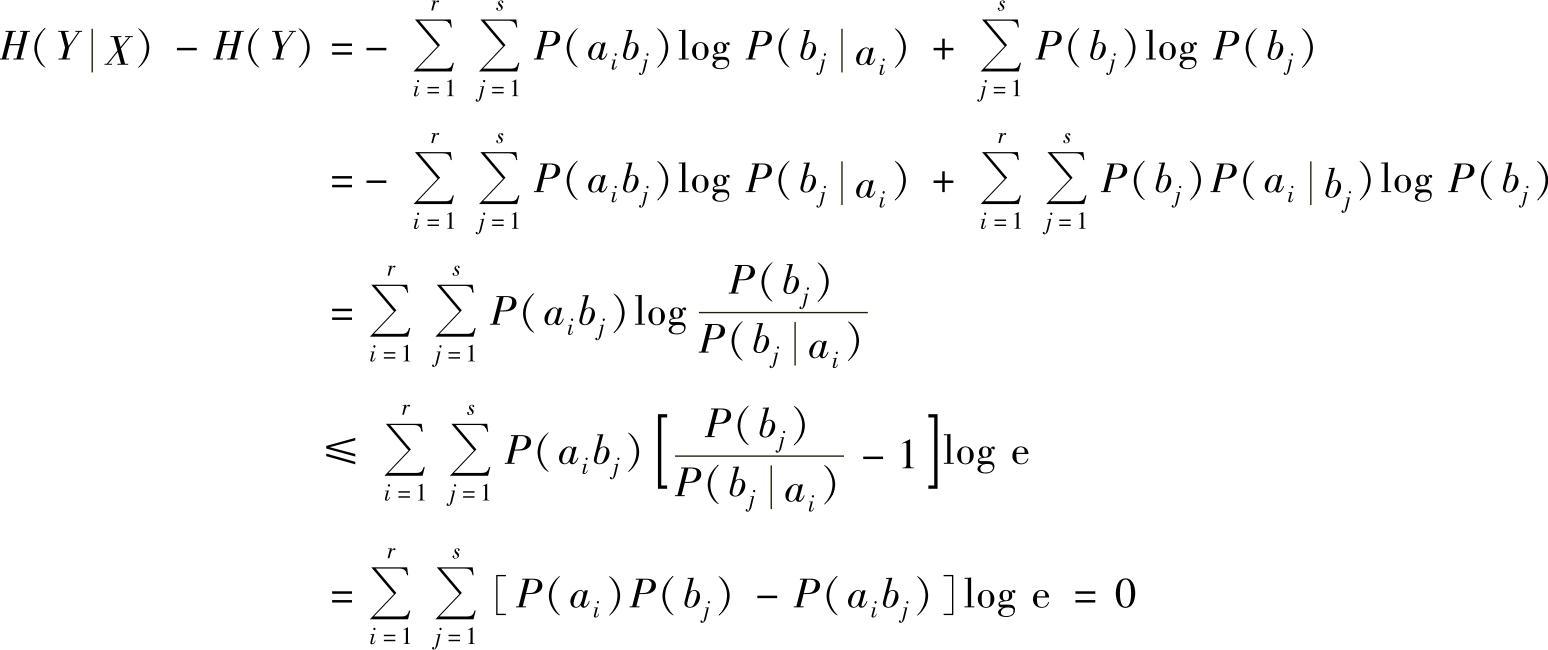
因此，有H（Y|X）≤H（Y）成立。同理可证H（X|Y）≤H（X）成立。

【证毕】

熵的不增原理表明，在信息处理过程中，条件越多或者信息处理的环节越多，信息熵越小。

性质2.19 联合熵和信息熵的关系为

H（XY）≤H（X）+H（Y）（2.41）

当X和Y相互独立时等号成立。

式（2.41）的关系可以方便地推广到N个随机变量的情况，即

H（X₁X₂…X_N）≤H（X₁）+H（X₂）+…+H（X_N） （2.42）

当X₁，X₂，…，XN相互独立时，等号成立。

由性质2.17（强可加性）和性质2.18可以直接证明性质2.19。

【例2.26】（续例2.21）

例2.21已计算信源X和Y的联合熵H（XY）、条件熵H（X|Y）和H（Y|X）。本例再计算信源X和Y的熵为

可以检验

以及H（X|Y）=0.8755＜H（X）=0.8813和H（Y|X）=0.9651＜H（Y）=0.9709。