随机事件的互信息和条件互信息详解

自信息衡量的是一个事件所含的信息量的大小，互信息则是衡量两个或者多个事件之间关系的紧密程度。

1.互信息的定义与含义

“互”信息，顾名思义，指的是多个事件之间的关系。例如在通信过程中，发信者发送一个消息x，且收信者收到一个消息y后，为分析这一过程中收信者所获得的信息量就需要研究两个离散随机变量X和Y之间的关系。互信息（也称为互信息量）衡量的就是这种关系大小的一种数学分析工具。

定义2.4 在离散联合随机变量集XY上，事件y（y∈Y）的出现给出关于事件x（x∈X）的信息量定义为互信息（或互信息量），其定义式为

互信息的单位与自信息的单位一样取决于对数的底。当对数底为2时，互信息的单位为bit。由式（2.13）可以得到

即

互信息量=自信息量-条件自信息量=原有的不确定性-仍然保留的不确定性

因此，互信息的含义是：

1）由事件y消除的关于事件x的不确定度。

2）由事件y提供的关于事件x的信息量。

3）事件x和y之间关系的密切程度。互信息的绝对值越大，x和y的关系越密切。

定义2.5 对于三维离散联合随机变量集XYZ，联合事件yz（yz∈YZ）的出现给出关于事件x（x∈X）的信息量定义为联合互信息（或联合互信息量），其定义式为

注：互信息I（x；y）中，事件x和y之间是用分号“；”分隔的，而联合自信息I（x，y）中，事件x和y之间是用逗号“，”分隔的，有时联合自信息也可以写成I（xy）。

2.互信息的性质

容易证明（性质的证明留作习题），互信息具有下述基本性质：

性质2.3 （对称性）互信息的对称性为

I（x；y）=I（y；x）（2.16）

互信息的对称性的含义是，由事件y提供的事件x的信息量等于由事件x提供的事件y的信息量。这一特性也是将I（x；y）称为互信息的原因。

性质2.4 当事件x和y统计独立时，互信息为零。

事件x和y统计独立使其互信息为零说明：不能从观测事件y获得关于另一个事件x的任何信息；或反之，也不能从观测事件x获得关于另一个事件y的任何信息。

性质2.5 互信息可以为正，也可以为负。

互信息为正，说明事件y的出现有利于事件x的出现；反之，互信息为负，说明事件y的出现不利于事件x的出现。

性质2.6 任何两个事件之间的互信息不大于其中任一事件的自信息量。

该性质说明互信息是描述传输特性的物理量，传输的量值不可能大于被传输的量值。这表明，某一随机事件的自信息是任何其他事件所能提供的关于该事件的最大信息量。

根据互信息的定义式，结合等式P（xy）=P（x）P（y|x）=P(y)P（x|y），可以推导出下面关系式：

式（2.17）～式（2.19）给出了互信息的三种不同表达式，表达了观察者从不同角度对事件x和事件y之间的互信息的描述。在实际应用中可以根据具体情况选用一种较为方便的表达式。互信息的引出，使信息流通问题进入了定量分析的范畴，为信息流通的定量测量奠定了坚实的基础。

【例2.11】

密码学中，假设将明文x加密为密文y，如果I（x；y）=0，则说明这个密码算法具有理论安全性，即绝对安全。这是因为明文x和密文y之间的互信息为0，根据密文，攻击者无法得到关于明文的任何信息。

【例2.12】

a先生预先知道b、c、d三位先生中必定有一人于当晚到他家拜访，且三人来访的可能性相同。但是，上午a先生接到d先生的电话说因故不能来了，该电话事件记为e。下午a先生又接到c先生的电话，说也因故不能来了，该电话事件记为f。计算下列信息量：(www.xing528.com)

1）未接到电话前，a先生获得关于b、c、d三位先生来访事件的信息量。

2）接到d先生的电话后，a先生获得关于b、c、d三位先生来访的互信息。

3）再接到c先生的电话后，a先生获得关于b、c、d三位先生来访的互信息。

解1）未接到电话前，a先生获知b、c、d三位先生来访为等概事件，其先验概率为P（b）=P（c）=P（d）=1/3，来访事件的信息量为

2）接到d先生的电话，即发生事件e后，a先生获得b、c、d三位先生来访的后验概率为P（b|e）=P（c|e）=1/2，P（d|e）=0，其来访的互信息为

I（d；e）=∞说明事件e发生后d先生就不会拜访a先生了，若d先生一旦来拜访a先生，其提供的信息量就是无穷大。或者理解为，因P（d|e）=0，即在事件e发生条件下不会出现事件d，故无须考虑事件d与事件e之间的互信息。

3）再接到c先生的电话后，即发生事件f后，a先生获得b、c、d三位先生来访的后验概率为P（b|ef）=1，P（c|ef）=P（d|ef）=0，其来访的互信息为

由例2.12看出，由于I（b；ef）=1.585bit，I（b；e）=0.585bit，因此事件ef的出现有助于确定事件b的出现。

【例2.13】

设e表示事件“降雨”，f表示事件“空中有乌云”，且P（e）=0.125，P（e|f）=0.8。求：

1）事件“降雨”和“无雨”的自信息。

2）在“空中有乌云”条件下，“降雨”和“无雨”的自信息。

3）“降雨”与“空中有乌云”的互信息和“无雨”与“空中有乌云”的互信息。

解设e表示事件“无雨”，则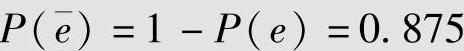，。则有

1）事件“降雨”的自信息I（e）和事件“无雨”的自信息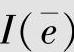分别为

2）在“空中有乌云”条件下，“降雨”的自信息I（e|f）和“无雨”的自信息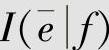分别为

3）“降雨”与“空中有乌云”的互信息I（e；f）和“无雨”与“空中有乌云”的互信息I（e；f）分别为

由例2.13看出，事件“降雨”本来不确定度很大（3bit），但由于事件“空中有乌云”的出现，不确定度减小（0.322bit），这是因为“空中有乌云”提供了关于“降雨”正的信息量（2.678bit）。相反，事件“无雨”本来不确定度较小（0.193bit），但由于事件“空中有乌云”的出现，不确定度反而变大（2.322bit），这是因为“空中有乌云”提供了关于“无雨”负的信息量（-2.129bit）。

3.条件互信息的定义与含义

定义2.6 对于三维离散联合随机变量集XYZ，在给定事件z（z∈Z）条件下，事件y（y∈Y）的出现给出关于事件x（x∈X）的信息量定义为条件互信息（或条件互信息量），其定义式为

性质2.7 联合互信息、条件互信息和互信息之间满足关系式：

证明 依I（x；yz）的定义式有

【证毕】

性质2.7表明，联合事件yz出现后所提供的有关事件x的信息量I（x；yz）等于事件z出现后所提供的有关x的信息量I（x；z），加上在给定事件z条件下再出现事件y所提供的有关x的信息量I（x；y|z）。

【例2.14】（续例2.12）

计算a先生接到d先生电话（事件e）条件下，又接到c先生的电话（事件f）后所获得的关于b、c、d三位先生来访的条件互信息。

解由例2.12知，a先生接到d先生电话（事件e）后获得b、c、d三位先生来访的后验概率为P（b|e）=P（c|e）=1/2，P（d|e）=0；再接到c先生的电话（事件f）后，a先生获得b、c、d三位先生来访的后验概率为P（b|ef）=1，P（c|ef）=P（d|ef）=0。因此，b、c、d三位先生来访的条件互信息为

而由于P（d|e）=0，条件互信息I（d；f|e）无意义。此外，由性质2.7可以验证