信息论基础：信源的数学模型

信源是信息的来源，是产生消息或消息序列的源泉。信息是抽象的，消息是具体的，但消息不是信息本身，消息包含着和携带着信息。因此，需要通过消息——信息的表达者来研究信源。Shannon信息论不研究信源的内部结构，不研究信源是如何产生和怎样产生各种不同的、可能的消息，仅研究信源的各种可能的输出消息，以及输出各种可能消息的不确定度。

信息可以看成是消除不确定度的东西。在通信系统中收信者在未收到消息以前，对信源发出什么消息是不确定的、随机的，可以用随机变量、随机序列（随机矢量）或随机过程来描述信源输出的消息，或者说用样本空间及其概率测度——概率空间来描述信源。

根据概率论的知识，有下列两种概率空间用于描述信源：

（连续型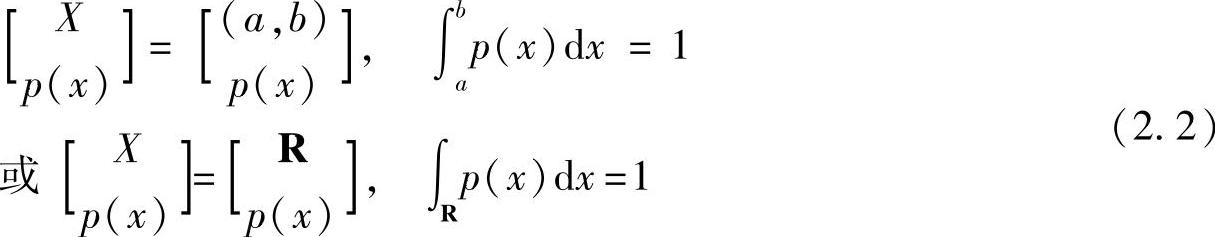） (www.xing528.com)

式中，X是随机变量，对于离散型，X的值域为符号集A：{a₁，a₂，…，a_r}，r是A中的符号个数，r=‖A‖；对于连续型，X的值域为（a，b）之间的所有实数或为实数域R（有无限多个取值）。P（a_i）是离散型随机变量X的输出符号（事件）a_i（i=1，2，…，r）的概率（也称为先验概率），并称为X的概率分布；p（x）是连续型随机变量X的概率密度函数。

式（2.1）是离散型概率空间，将该空间的所有可能选择的消息集合A：{a₁，a₂，…，a_r}称为（离散型）随机变量X的样本空间。式（2.2）是连续型概率空间，将该空间的所有可能选择的消息集合A：（a，b）或R称为（连续型）随机变量X的样本空间。