2.1.1概率论符号约定和概率知识基础

在信息论中常用到概率论的基本概念和性质，为此，先对这些概念和性质进行简要的复习。先给出随机变量的符号约定。

（1）离散事件的符号约定

离散随机变量用X和Y表示，其值域分别为符号集合（或符号集、集合）A：{a₁，a₂，…，a_r}和B：{b₁，b₂，…，b_s}。X和Y各自发生的事件（或随机事件、离散事件、离散随机事件）分别用x和y表示，或用a_i和b_j表示。需要说明的是，事件x和y泛指X和Y发生一个事件，且x∈A，y∈B；而事件a_i和b_j特指X和Y分别发生一个特定事件x=a_i和y=b_j。

离散随机变量序列用X=（X₁，X₂，…，X_N）和Y=（Y₁，Y₂，…，Y_N）表示；X的分量X_i（i=1，2，…，N）的值域为A：{a₁，a₂，…，a_r}，Y的分量Y_i（i=1，2，…，N）的值域为B：{b₁，b₂，…，b_s}。X和Y各自发生的事件（或序列事件、矢量事件）分别用x=（x₁，x₂，…，x_N）和y=（y₁，y₂，…，y_N）表示，或用α_i=（a_i1，a_i2，…，a_iN）和β_j=（b_j1，b_j2，…，b_jN）表示。同样需要说明的是，x和y泛指X和Y发生一个序列事件，其分量也是泛指的，分量的下标表示该分量在序列中的序号；而事件α_i和β_j特指X和Y分别发生一个特定事件x=α_i和y=β_j，且α_i和β_j的分量下标的下标表示该分量在序列中的序号。

（2）连续事件的符号约定

连续随机变量用X和Y表示，X的值域为符号集A：（a，b）或A：R，Y的值域为B：（a′，b′）或B：R，其中R表示全体实数集合（实数域）。X和Y各自发生的事件（或随机事件、连续事件、连续随机事件）分别用x和y表示，或用x_i和y_j表示。

连续随机变量序列用X=（X₁，X₂，…，X_N）和Y=（Y₁，Y₂，…，Y_N）表示；X的分量X_i（i=1，2，…，N）的值域为A：（a，b）或A：R，Y的分量Y_i（i=1，2，…，N）的值域为B：（a′，b′）或B：R。X和Y各自发生的事件（或序列事件、矢量事件）分别用x=（x₁，x₂，…，x_N）和y=（y₁，y₂，…，y_N）表示，且x和y泛指X和Y发生一个序列事件，其各分量的下标表示该分量在序列中的序号。一般地，连续随机变量序列是由连续随机变量进行取样得到的取样序列，因此，序列中各分量的下标是离散时间（取样时刻）。

接下来给出离散事件的概率论基础知识。

（1）无条件概率

离散随机变量X和Y各自分别发生事件（或随机事件）x=a_i和y=b_j的概率为

称P（a_i）和P（b_j）分别为X和Y的无条件概率或先验概率；称P（a₁），P（a₂），…，P（a_r）或P（x）为离散随机变量X的概率分布；称P（b₁），P（b₂），…，P（b_s）或P（y）为离散随机变量Y的概率分布。

（2）联合概率

在离散联合集XY上，设随机变量XY的值域为集合{a_ib_j|i=1，2，…，r；j=1，2，…，s}，随机变量XY发生联合事件（或联合随机事件）xy的概率为

P_X，Y（a_ib_j）=P_X，Y（x=a_i，y=b_j），简记为P（a_ib_j）或P（xy）

称P（a_ib_j）为XY的联合概率；称P（a₁b₁），P（a₁b₂），…，P（a_rb_s-1），P（a_rb_s）或P（xy）为离散联合集XY的联合概率分布。

（3）条件概率

在离散联合集XY上，在事件x=a_i条件下发生事件y=b_j（该事件可以简记为y=b_j|x=a_i或b_j|a_i）的概率为

P_Y/X（b_j|a_i）=P_Y/X（y=b_j|x=a_i），简记为P（b_j|a_i）或P（y|x）

或在事件y=b_j条件下发生事件x=a_i（该事件可以简记为x=a_i|y=b_j或a_i|b_j）的概率为(www.xing528.com)

P_X/Y（a_i|b_j）=P_X/Y（x=a_i|y=b_j），简记为P（a_i|b_j）或P（x|y）

称P（b_j|a_i）和P（a_i|b_j）为条件概率；称P（b₁|a₁），P（b₂|a₁），…，P（b_s-1|a_r），P（b_s|a_r）或P（y|x）为离散联合集XY上在离散随机变量X条件下离散随机变量Y的条件概率分布。相对于先验概率P（a_i）而言，有时称P（a_i|b_j）为后验概率。

在上述的无条件概率、联合概率和条件概率的表达式中，在没有歧义时可以采用简记式表达。

（4）无条件概率、条件概率和联合概率满足的性质和关系

1）0≤P（a_i），P（b_j），P（b_j|a_i），P（a_i|b_j），P（a_ib_j）≤1。

2）。

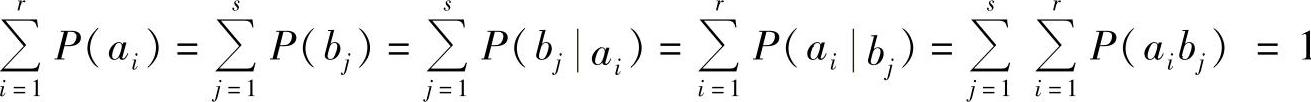3）。

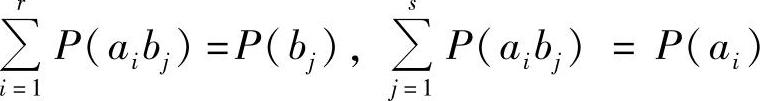4）P（a_ib_j）=P（a_i）P（b_j|a_i）=P（b_j）P（a_i|b_j）。

5）当X与Y相互独立时，P（b_j|a_i）=P（b_j），P（a_i|b_j）=P（a_i），P（a_ib_j）=P（a_i）P（b_j）。

6）。

最后，给出连续事件的概率论基础知识。

离散事件用概率进行测度，而连续事件需要用概率密度函数或概率分布函数进行测度。连续随机变量X和Y各自的一维概率密度函数为

一维概率分布函数为

称p（x）和p（y）分别为X和Y的无条件概率密度函数或先验概率密度函数；称F_X（x）为连续随机变量X的概率分布函数；称F_Y（y）为连续随机变量Y的概率分布函数。

连续随机变量X和Y的联合概率密度函数记为p_X，Y（x|y），简记为p（xy）。连续随机变量X和Y之间的条件概率密度函数记为p_Y|X（y|x）和p_x|y（x|y），简记为p（y|x）和p（x|y）。

无条件概率密度函数、条件概率密度函数和联合概率密度函数满足下列性质和关系：

5）当X与Y相互独立时，p（y|x）=p（y），p（x|y）=p（x），p（x|y）=p（x）p（y）。

注：本书约定，离散随机事件的概率和连续随机变量的概率分布函数用大写“P（）”表示，如P（a_i）、P（y）、P（b_j|a_i）、P[x≤x₁]等；连续随机变量的概率密度函数用小写“p（）”表示，如p（x）、p_Y|X（y|x）等；有时，也用单符号小写“p”表示离散随机事件的概率，如p_i、p_i，j等。