机敏材料压阻性能理论模型优化探究

实验研究表明，导电复合材料的压阻效应与基体性质、导电相粒子的粒径和掺量，以及所受到的压力大小等有关。水泥基导电复合材料当其导电相掺量在渗滤阈值附近时具有良好的压阻特性。基于隧道效应电导理论，水泥基导电复合材料的应变感知性能机理为应变引起导电相粒子之间距离的变化，这一变化将导致导电相粒子间的电阻率发生变化。由于导电相粒子在水泥基复合材料中所形成的导电网络由无数个导电链经串、并联组成，呈随机空间状态分布，其中任两个导电粒子间隙的空间方位不一定与电阻测试方向平行，任两个导电粒子之间的“应变”大小与复合材料电阻测试方向应变并不完全相同。因此，水泥基导电复合材料的压阻特性与其多轴变形有关，而非仅与加载方向或电阻测试方向的变形有关。因此，分析水泥基导电复合材料试样在多轴变形状态下的力电理论，对分析其应变感知特性具有重要意义。本节基于隧道效应电导理论，考虑导电粒子间隙的空间性，对多轴应变状态下导电试样的力电理论进行了分析。

根据隧道效应理论方程，可以知道两个导电粒子之间的间隙隧道电阻与间隙应变的关系。如果已知在多轴应变下间隙应变与复合材料整体应变的关系，按照复合材料电阻率可由间隙隧道电阻表征的原理，就可得出复合材料电阻与应变的关系。由于隧道效应理论要求粒子间隙宽度应在一定范围之内，已有的理论研究和本文实验研究均表明导电相掺量在渗滤阈值附近的复合材料导电机理符合隧道效应理论。因此，下面的分析主要针对掺量在渗滤阈值附近的复合材料。

当掺量达到渗滤闭值附近时，导电粒子将形成比较完善的导电网络。由于隧道电流仅发生在很小的表面区域内，因此在导电网络中，认为导电粒子之间的距离为其表面之间的最短距离。在多轴受力状态下，导电链中各导电相间隙长度的变化情况是不同的，与间隙的空间方向有关。导电网络由很多条导电链组合而成，而且每条导电链由许多个方向各异的导电相间隙及导电粒子组成。相对于隧道电阻而言，导电粒子的电阻可以忽略不计。因此，可将导电相的间隙视为电阻。

水泥基机敏复合材料是由导电相和水泥基体通过一定的方式结合在一起构成的，因此该复合材料的电阻应当是导电相和水泥基体电阻的函数。根据有关压力-电阻模型分析［59］，假设水泥基体的电阻值一定，且其自身电阻远远大于导电相的电阻，并假设导电相在水泥基体中为理想状态下的均匀分布，则机敏材料内部在平行于导电通路方向上的电流可以忽略。因此，机敏复合材料的电阻主要由水泥基体中导电相的数量及连贯导电通路的数目来决定，公式为：

式6-10中，R为机敏复合材料的电阻；Ra为两相邻导电相间的电阻；Rb为一个导电相的电阻；x为水泥基体中一条平行于电流方向导电通路中导电相的数目；y为水泥基体中平行于电流方向的导电通路数目。假设导电相为球状，如图6-3所示。

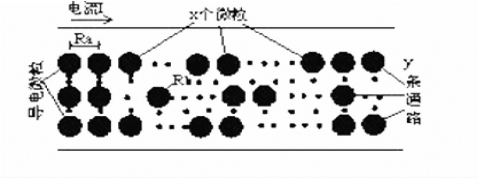
图6-3　导电相在水泥基体中的理想分布图

导电相掺量较大的复合材料的导电网络是由导电链通过串并联的方式组成的，而导电链由导电粒子及其间隙形成。在每条导电链中，导电相间隙的空间方位是随机分布的。由于粒子间隙数量巨大，因此可认为间隙在各方向上为均匀分布。如果以每条导电链为一个单位，并认为各导电链均由包括了各个空间角度的导电相间隙串联而成，则每个导电链可视为一个大电阻，其阻值等于各个导电相间隙电阻之和。复合材料的电阻由导电链电阻经过复杂的串并联关系求得。在复杂应变条件下，导电链电阻也会随之发生变化。

如果水泥基体中导电相间距太大的话，电子将无法穿过其间势垒进行传导；而当导电相间距较小时，电子能够穿越势垒形成隧道电流I表示为：

式6-11中，V为外加低电压；d为绝缘阻隔层的厚度；H为相邻导电相间的势垒高度，它可以由导电相和水泥基体的功函数相减得到；m和e分别代表电子的质量和电荷；h代表普朗克常数。由于隧道电流I与绝缘阻隔层厚度d有显著地依赖关系，可以认为隧道效应是发生在两导电相靠近处的狭窄区域内，我们把这个极窄区域内相邻导电相间的最小距离称之为相距，用字母d表示。假设发生隧道效应处绝缘阻隔层的有效截面积为S2，则该区域两个相邻导电相间的电阻Ra可以表示为：

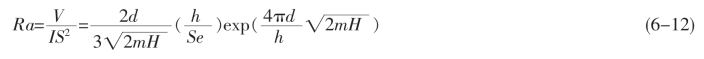
由于导电相的导电能力大大高于水泥基体，在此认定其电阻Rb近似为零。于是，将式6-12代入式6-10中，可得水泥机敏复合材料的电阻有以下关系：

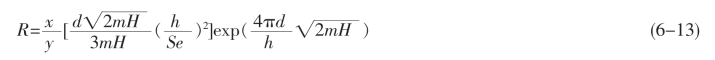
这样通过式6-13可得到水泥机敏复合材料电阻的理论值。当水泥机敏复合材料受到压应力作用时，该材料被压缩，由于导电相和水泥基体的可压缩率不同，导致导电相间的距离会发生变化，由式6-13可知，水泥机敏复合材料的电阻值也会跟着变化。假设导电相的间距从d0变到d，该复合材料的电阻从R0变到R，则相对电阻变化可以表示为如下：(www.xing528.com)

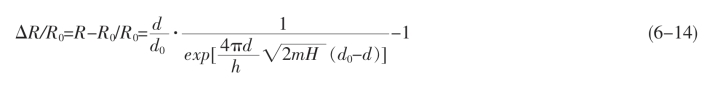
式6-14中，d0为初始导电相间距；R0为水泥机敏复合材料的初始电阻值；其他参数同上面所述一致。式6-14与式6-13相比，较难得到精确值的参数x、y、d和S2均不存在了，因此计算相对电阻变化ΔR/R0比直接计算该复合材料电阻值R精确得多，使得测量结果更接近实际。此外，在实际应用中，最重要的参数就是机敏复合材料电阻随压应力的相对变化率ΔR/R0，所以只对该复合材料相对电阻随外加压力的变化及其时间依赖性进行讨论。

由于水泥基体的压缩模量远大于导电相的压缩模量，因此在计算导电相间距变化时，只需考虑水泥基体的形变，而导电相在外加应力下的变形可以忽略。如果外加压力是单轴压力，导电相间距可以表示为：

式6-15中，σ为压应力；E为水泥基体的压缩模量；ε为对应水泥基体的应变。为了计算简便，假设导电相呈球状，尺寸相同，并且在该水泥基体中呈立方晶格分布，则导电相的原始间距d0可以用下式表示：

式6-16中，β是导电相占该复合材料的体积含量；D是导电相的直径。式6-16已被大量地运用于机敏复合材料电学性能和力学性能的研究中。因此关于导电相在水泥基体中的立方晶格分布的假设在该复合材料压阻特性的讨论中是可行的。

将式6-16和式6-15代入式6-14中，得到机敏复合材料电阻与外加应力的关系，即压阻特性：

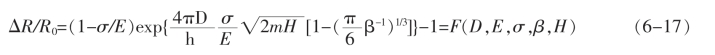
由式6-17可见，水泥机敏复合材料的压阻特性主要与水泥基体压缩模量E、外加应力σ、导电相间的势垒高度H、导电相的直径D和水泥基体中导电相的体积含量β这五个因素有关，当任何一个因素发生变化时，该复合材料的压阻特性就会发生相应变化。式6-17中，是电阻相对变化关于自变量D、E、σ、β和H的函数。

在外加应力σ下，ΔR/R0会变小，即出现压力依赖性。相同外加应力下，导电相的直径或相邻导电相间势垒高度的增加均会使电阻减小得更快，即电阻的压力依赖性增大了；同时，水泥基体的压缩模量或导电相的体积含量的增加会减弱电阻的压力依赖性。此结论与实验结果相符。

碳纤维和石墨作为导电相材料，具有优良的物理化学稳定性，所以达到渗流阈值掺量的碳纤维石墨水泥砂浆试块电学性能稳定。目前，对于其导电机理的解释主要有导电通路理论、隧道效应理论和场致发射理论。本文所用碳纤维为直径为Φ7μm、长5mm的短切状碳纤维，石墨为细小鳞片状颗粒，当他们作为导电相材料加入到水泥砂浆混合料中时，机敏材料的导电机理有下列几种情况：（1）一部分导电粒子通过相互接触而形成链状导电通路，使碳纤维石墨水泥砂浆试块可以导电，即导电通路效应。（2）另一部分导电粒子则以孤立粒子或小聚集体的形式分布在水泥、砂子混合料中，基本不参与导电。如果这些孤立粒子或小聚集体之间的间距很近，仅被一层很薄的水化产物隔开时，那么由于热振动而激活的电子就能越过薄层而跃迁到相邻的导电粒子上，形成较大的隧道电流，即隧道效应。（3）当导电粒子间的内部电场很强时，电子跨越薄层势垒的概率就很大，从而产生电场发射电流，即场致发射效应。因此，可以认为碳纤维石墨水泥砂浆材料的导电性是导电通路效应、隧道效应和场致发射效应共同作用的结果。当碳纤维和石墨掺量及输入电压不同时，3种导电机理对于导电水泥基复合材料的整体导电行为的贡献率也不同。图6-4为碳纤维石墨水泥砂浆微观分析的照片，以观察石墨颗粒、碳纤维的微观形貌及其在水泥砂浆中的具体分布情况。从图6-4中可以看出碳纤维呈圆柱状、石墨以鳞片状均匀分布于水泥基体中，碳纤维、石墨与水泥基体之间均具有较好的粘结。碳纤维石墨水泥砂浆的微观分析，证明了上述导电现象分析的正确性。

图6-4　碳纤维1.0%、石墨20%在碳纤维石墨水泥砂浆中的分布

影响石墨水泥基复合材料的压敏特性的因素很多，包括水泥基体的性质和显微结构、石墨的性质及其分散性、试样的制备工艺等。当掺加石墨粒子的砂浆在压力作用下时，砂浆内的导电通路随压力增大，而且石墨粒子间距随压力变小，隧道效应越来越强。这两方面的作用将引起石墨水泥砂浆电阻率随压力的不断下降而使其具有了压敏性能。石墨粒子掺量越多，受压时形成的导电通路越多、跃迁的电子越多，对压敏特性的贡献越大。加入CCCW的水泥基体的性质和显微结构对复合材料导电性的影响与孔结构的减少有关。这是由于水泥基体的内部孔隙被进一步地填充，离子的迁移空间减小，导致导电能力减弱，从而使极化效应减弱，电阻值稳定性提高。

影响碳纤维石墨水泥砂浆的压敏特性的因素很多，包括水泥基体的性质和显微结构、碳纤维和石墨的性质及其分散性、试样的制备工艺等。目前国内外对于水泥基复合材料压敏性的产生机制，有许多观点。有些学者已做了大量的试验，认为是纤维从水泥基体中的拉拔引起接触电阻变化而产生的。然而有些学者则认为是量子隧道效应而产生的，即受到压应力作用时，功能组分之间的间距会减小，从而导致势垒宽度变窄，隧穿电流增加，宏观电阻相应减小。