如何提高蓄电池实际容量？

在规定的条件下，完全充电的（fully charged）蓄电池能够提供的电量叫做蓄电池的容量（capacity），通常用安时（A·h）表示。所谓规定的条件，一般是指放电电流（discharge current）强度、蓄电池的温度、终止电压（final voltage；cut—off voltage）和电解液浓度等的值。

在恒流放电（constant current discharge）的特定情况下，容量C（A·h）等于放电电流强度I（A）与放电时间t（h）的乘积，即C=It，一般情况下有

假定电极上全部活性物质按照蓄电池的电池反应都参加电化学变化，根据法拉第定律计算出来的电量叫做蓄电池的理论容量（theoretical capacity）。蓄电池在一定条件下实际放出的电量（实际容量）一般不超过理论容量的50%～60%。

根据铅酸蓄电池放电时的电化学反应

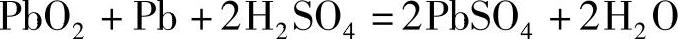
理论上1mol PbO₂、1mol Pb和2mol H₂SO₄组成的蓄电池能够放出2F（2×26.80A·h）的电量。实际上这么多的活性物质构成的电极和电解液仅能放出理论电量的一半左右。在上一章，我们已经叙述过限制铅酸蓄电池放电的诸多因素。

在规定的条件下，蓄电池完全充电后所能提供的由制造厂标明的安时电量叫做蓄电池的额定容量（rated capacity）。标称容量（nominal capacity）是用来鉴别蓄电池的适当的近似的安时电量。

用C_r（A·h）表示蓄电池的额定容量，恒流放电的时间为t（h），那么放电电流I（A）可用下式表示：

习惯上把I（A）称为t小时率放电电流，简称为t小时放电率。在大电流放电的情况下，即I（A）在数值上是C_r（A·h）的n倍，则把I（A）称为n倍率放电电流，称这一过程为n倍率放电（有时n<1也习惯地称n倍率放电）。

蓄电池的容量依赖于电极上活性物质的量与结构、电解液的量与浓度、电极与电解液的温度、放电电流强度以及蓄电池的结构等因素。

蓄电池的放电容量C（或放电时间t）和放电电流I的关系，许多人提出过经验方程。其中普克特（Peukert）在1898年提出的方程

K=tIⁿ或t=KI^-n （8-3）也可表示为C=KI^（1-n）被广泛承认并实际应用^【1】。式中n和K是两个不同的常数，t以h（小时）为单位，I以A（安培）为单位。普克特当时提出铅酸蓄电池的常数n=1.30。

20世纪50年代以前，涂膏式铅酸蓄电池的极板厚度（指起动用蓄电池）较大、板栅厚度在2mm以上，极板厚度则接近3mm，尤其是正极板。对于这种蓄电池，取n=1.30，用普克特方程计算相对容量是颇为精确的。只要实际测定出蓄电池在两种不同的放电电流I₁和I₂的放电时间t₁和t₂，就可以解联立方程

而求出两个常数K和n。结果是

和logK=nlogI₁+logt₁ （8-7）

这里有一个实际例子。一组VRLA 2V 450A·h恒流放电。当放电电流为45.00A时，平均放电时间为15.18h；当放电电流为90.00A时，平均放电时间为6.839h。分别按式（8-6）和式（8-7）求出n=1.150和K=1207。表示这一组VRLA的放电电流与放电时间函数关系的普克特方程就是

t=1207I^-1.150由此就可以求出这一组VRLA在不同的放电电流值的放电时间和在不同的放电时间值的放电电流值。如当

I=2000A时，t=0.1823h（10.94min）而 t=20.00h时，I=35.32A这说明这一组VRLA以2000A放电，约相当于11min率；而其真实的20h容量则为20h×35.32A=706.4A·h。

后来有人在研究蓄电池正、负极板放电瞬变值时指出^【2】，在一定温度下，在电流密度为0.02～0.2A·cm^-2时，普克特方程是正确的，n值为1.4。

在一定温度下，n值取决于蓄电池结构。n关系到蓄电池容量随着放电电流增大而降低的变化速率。这由式（8-3）可以看出。式（8-3）可以写成

logt=logK-nlogI（8-8）由此得到

由式（8-9）可以认为n是logt对于logI变化的速率，负号表示式（8-8）是单调下降的。

在蓄电池结构的诸因素中，极板厚度是放电电流强度影响放电时间的首要因素。表8-1列出不同厚度的涂膏式极板铅酸蓄电池，在常温下两种不同放电电流强度下的放电时间及由此按照式（8-6）和式（8-7）计算出来的n和K的值。表中数据是同一实验中几只蓄电池放电数据的平均值。

表8-1 不同厚度极板的铅酸蓄电池的n和K的值

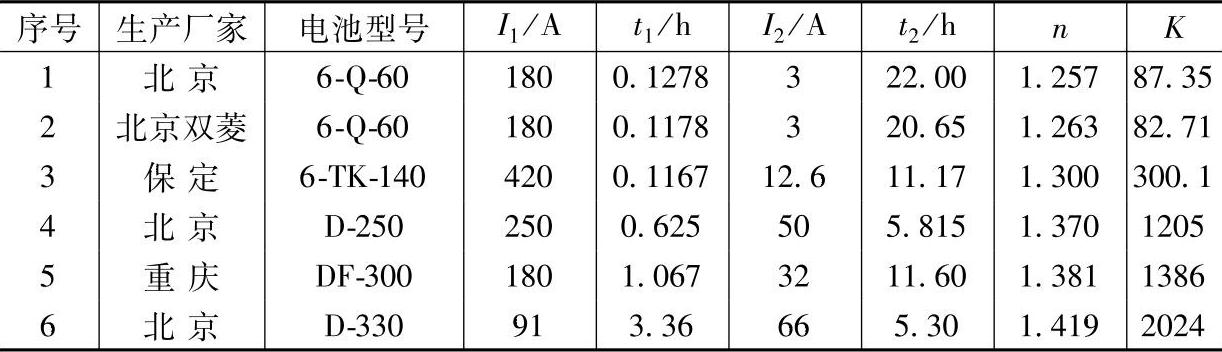
表8-1中后三种蓄电池虽然不是起动用蓄电池，但其正、负极板也都是涂膏式。表中序号3这一行中的数据引自参考文献^【3】。序号5这一行中的数据是重庆蓄电池总厂1985年6月的实验数据^【4】，其余的数据由著者实验得到。如果我们把得到的n值与蓄电池极板厚度作比较，就会发现它们之间似乎存在着有趣的规律性。

表8-2中的序号所指的蓄电池和表8-1相同。显然，n值随着正极板厚度的增加而单调增加。如果用δ（mm）表示正极板厚度，以δ为自变量，以n作为函数，对于涂膏式极板铅酸蓄电池，在常温下，用式（8-10）计算n值与表8-1中n的实验值是很接近的^【5】。

表8-2 铅酸蓄电池极板厚度与n值的关系

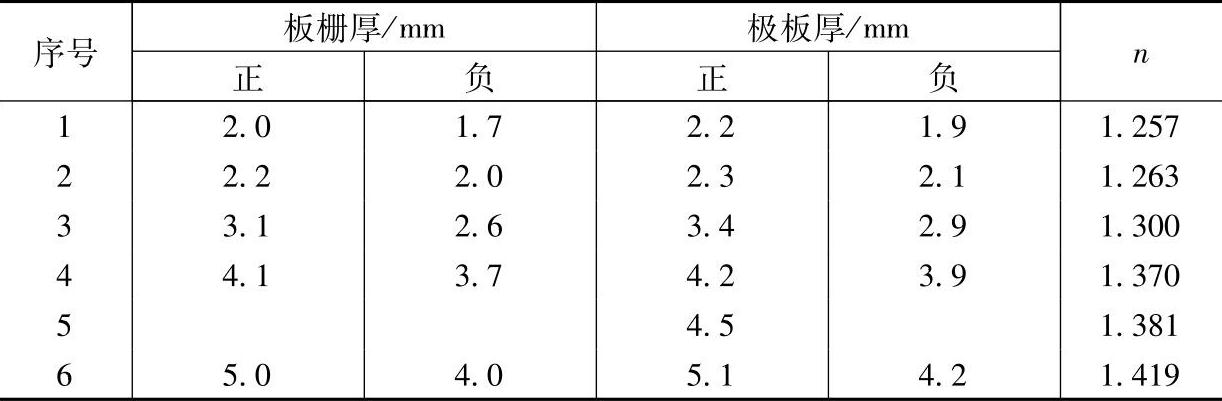
n=0.057δ+1.13 （8-10）

由于普克特方程已被广泛承认，表8-1中的n值是根据实验数据按照这一方程计算出来的，可以称为实验值，而用式（8-10）计算出来的n值则称为计算值。两种n值的比较见表8-3。

表8-3 普克特方程中n的实验值与计算值的比较

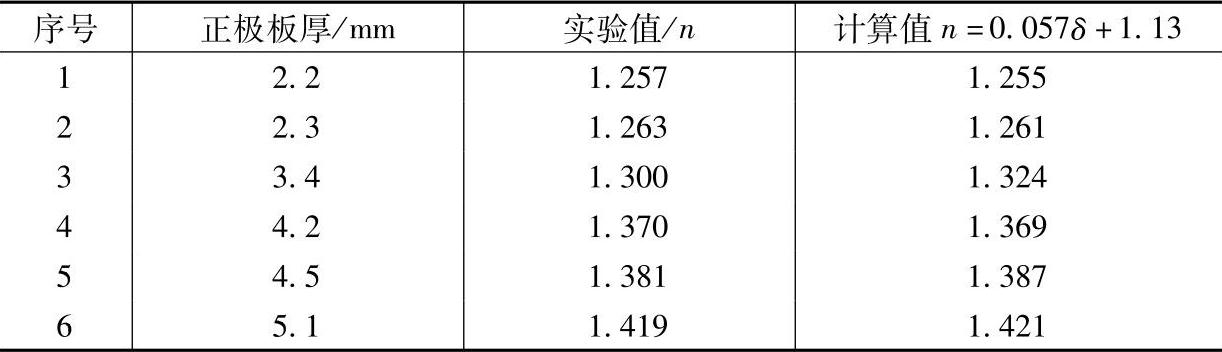
表8-3中的序号所指的蓄电池和表8-1相同。图8-1中，n=0.057δ+1.13是一条斜率为0.057、截距为1.13的直线。它与n的实验值较好地符合一致。这一粗略的经验式，也只对传统的富液式蓄电池才适合。

由于不同结构的蓄电池的常数n的差异，某种放电率时的蓄电池的相对容量会因蓄电池结构不同而不同。经典著作中给出的数据^【6】可以作为参考但并不普遍适用。这里计算一下不同n值的蓄电池在不同放电率的相对容量，以20h率容量为基准。

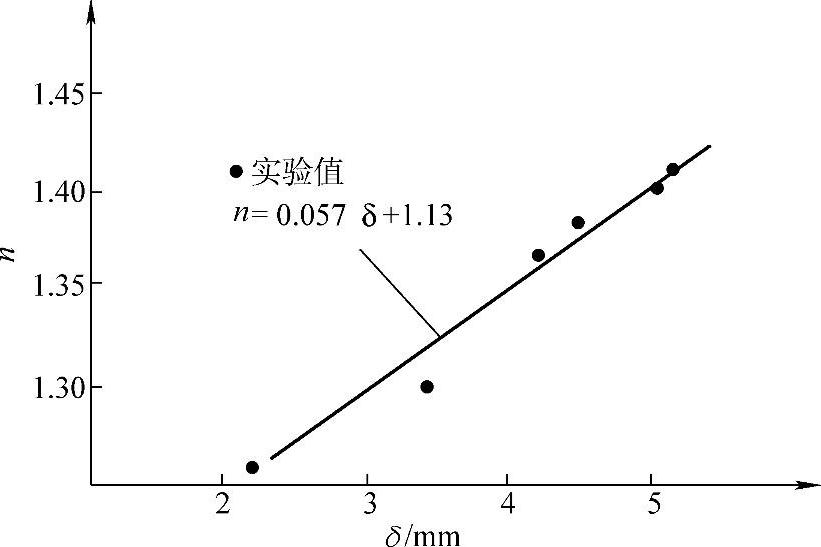
图8-1 普克特方程中常数n与极板厚度δ的关系

由普克特方程出发，当t=20h，I=I₂₀A时，有

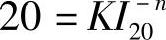
变换为

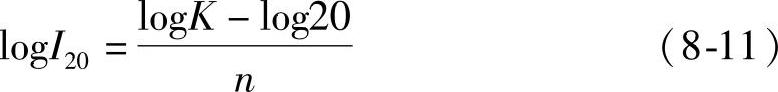
当放电时间缩短为20h的1/m即t=20/m（h）时，此时的放电电流用I₂₀/m表示，普克特方程为

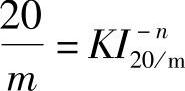
变换为log20-logm=logK-nlogI₂₀/m

即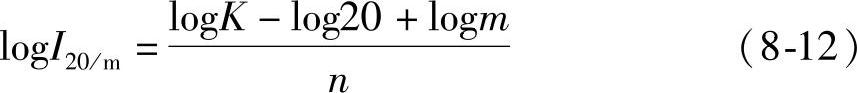注意到式（8-11）logI₂₀的表达式并将其代入式（8-12），式（8-12）变为

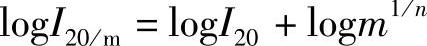
即I₂₀/m=m¹/n·I₂₀ （8-13）用式（8-13）可以求出任何放电率的放电电流。例如，欲求放电时间缩短为20h的一半，即m=2（此时为10h率放电时的放电电流），假定n=1.30，代入式（8-13）可求出

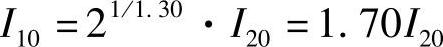
即10h率放电电流是20h率放电电流的1.70倍。10h率放电容量10I₁₀（即10×1.70I₂₀）是20h率放电容量20I₂₀的85.0%。

某种类型的蓄电池以不同的放电电流能工作多长时间（或容量多少）以及要求一定的放电电流和工作时间应选用哪种型号蓄电池，是蓄电池生产厂家遇到的用户常问到的问题。如果都以n=1.30来计算并回答问题，很可能与实际情况有出入。表8-4列出m分别为2（10h率）、4（5h率）、20/3（3h率）、20（1h率）、40（30min率）、60（20min率）、120（10min率）、240（5min率）时不同的n值的蓄电池在常温下的放电电流和相对容量（20h率容量为100）。

可以看到，n值（它与极板的厚度有关）对于较小放电电流（如10h率）的放电容量的影响较小，而对于大电流（如5min率）的放电容量影响较大。当n从1.25变化至1.40时，10h率相对容量从87.0%变化至82.0%，而5min率相对容量则从33.4%变化至20.9%。

表8-4所表明的是指定放电时间，蓄电池的放电电流及容量的相对值。更多的蓄电池用户感兴趣的是指定放电电流，蓄电池的放电时间和容量。仍从普克特方程t=KI^-n出发。当t=20时，放电电流I=C′₂₀/20A。这里C′₂₀是蓄电池的理论20h率容量，即蓄电池的普克特方程t=KI^-n中与t=20h相对应的自变量I与20的乘积（电流以A为单位，容量以A·h为单位）。这与蓄电池生产厂家所标称的额定容量C₂₀往往稍有差别。这样普克特方程变为

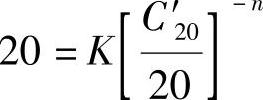
变换为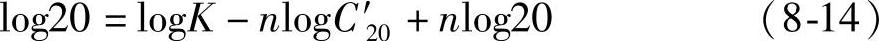

表8-4 常数n值不同的铅酸蓄电池（涂膏式极板） 常温下在不同放电率的相对容量

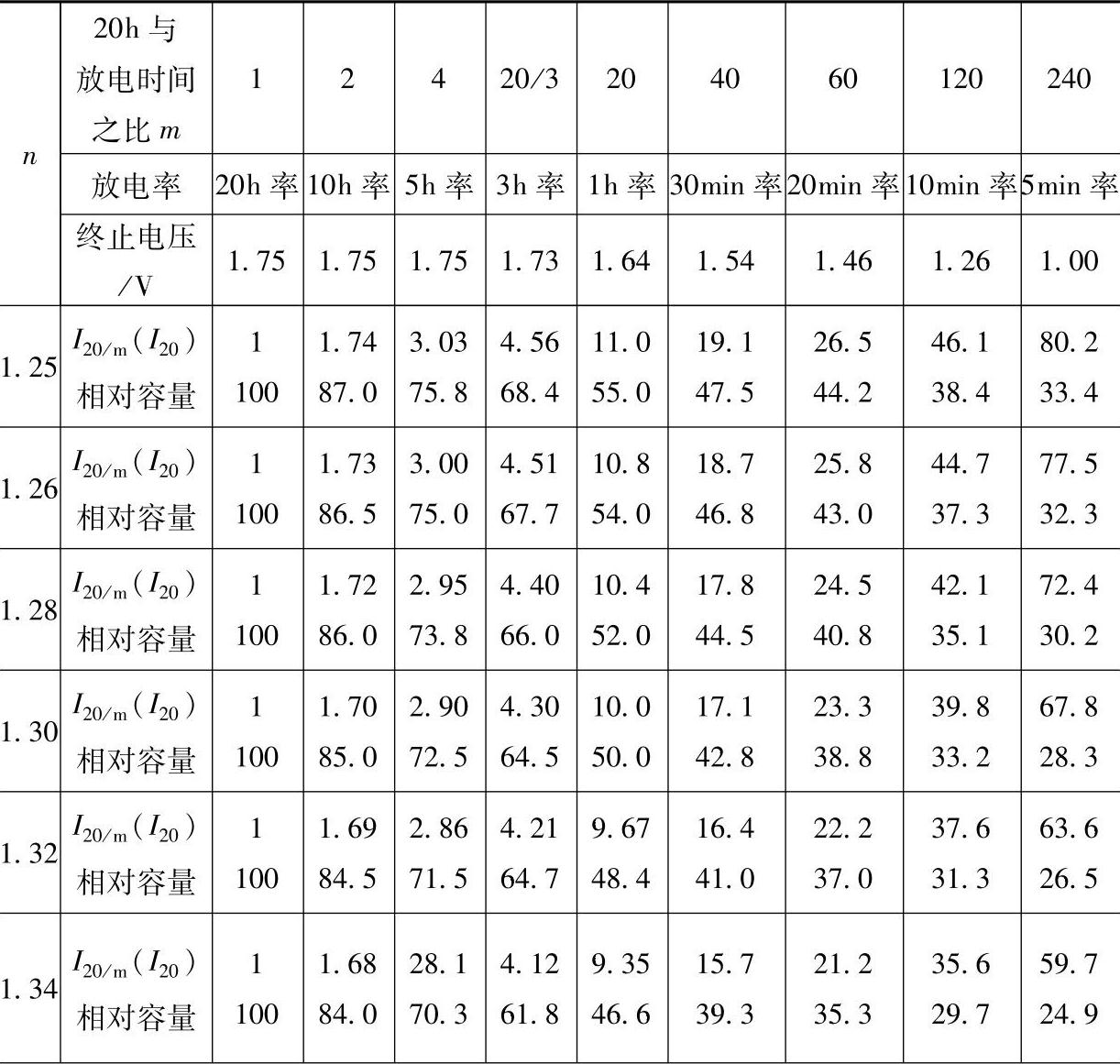
当放电电流增加到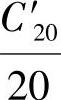的p倍，即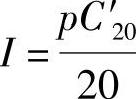时，放电时间用t_p表示为

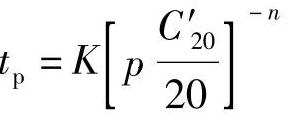
变换为 logt_p=logK-nlogC′₂₀+nlog20-nlogp（8-15）注意到式（8-14）中log20的表达式并代入式（8-15）得到

（续）

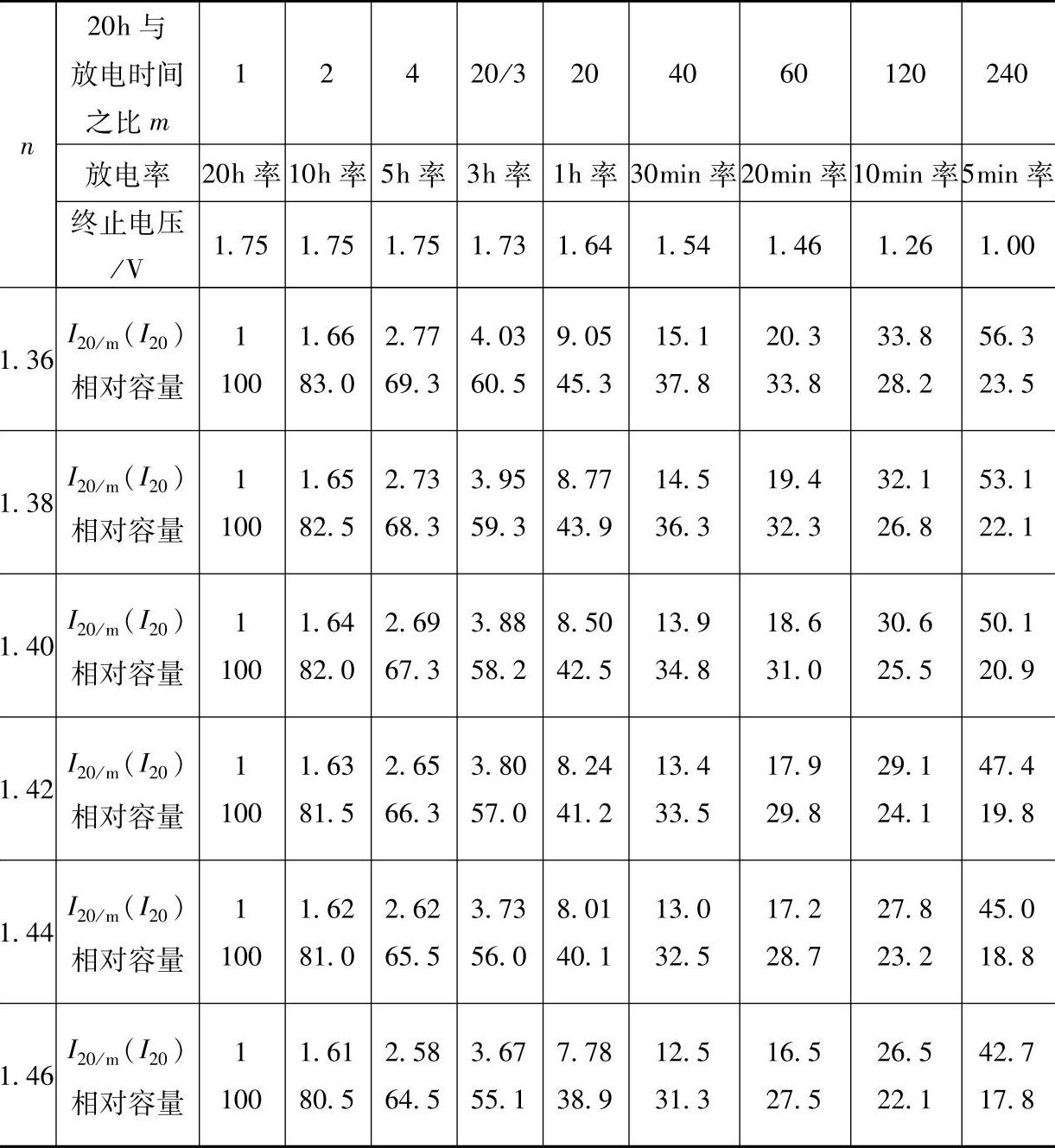
logt_p=log20-nlogp即logt_p=log20-logpⁿ即

用式（8-16）可以计算指定放电电流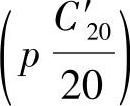时的放电时间。例如，对于n=1.30的蓄电池，当p=2即放电电流为C′₂₀/20的2倍时

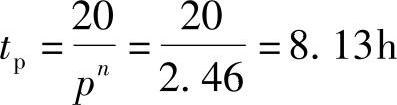
对于n=1.25的蓄电池，当p=2时

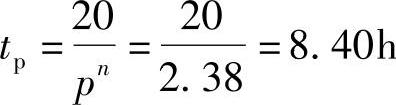
常温下具有不同的n值的蓄电池在不同的放电电流条件下的放电时间和相对容量（以放电电流为C′₂₀/20A时的容量为100）列在表8-5中。表8-1中六种蓄电池的理论20h率容量C′₂₀列在表8-6。

可以看到，同一n值的蓄电池的放电时间（或容量）随着放电电流的增加按指数规律下降。n值对大电流放电的容量的影响较大。如当n从1.25变化至1.40时，如果放电电流是C′₂₀的1/10，相对容量从84.1%变化至75.8%；如果放电电流为C₂′₀的3倍，相对容量则从35.9%变化至19.4%。

利用普克特方程计算蓄电池放电容量或放电时间的方法小结如下：

（1）蓄电池的20/mh率放电的放电电流I₂₀/m与20h率放电的放电电流I₂₀的关系是(www.xing528.com)

I₂₀/m=m¹/n·I₂₀

（2）蓄电池以pI₂₀（A）放电的放电时间t_p与20h率放电的放电时间（20h）的关系是

t_p=20/pⁿ

表8-5 常数n值不同的铅酸蓄电池（涂膏式极板）常温下在不同放电电流条件下的放电时间和相对容量

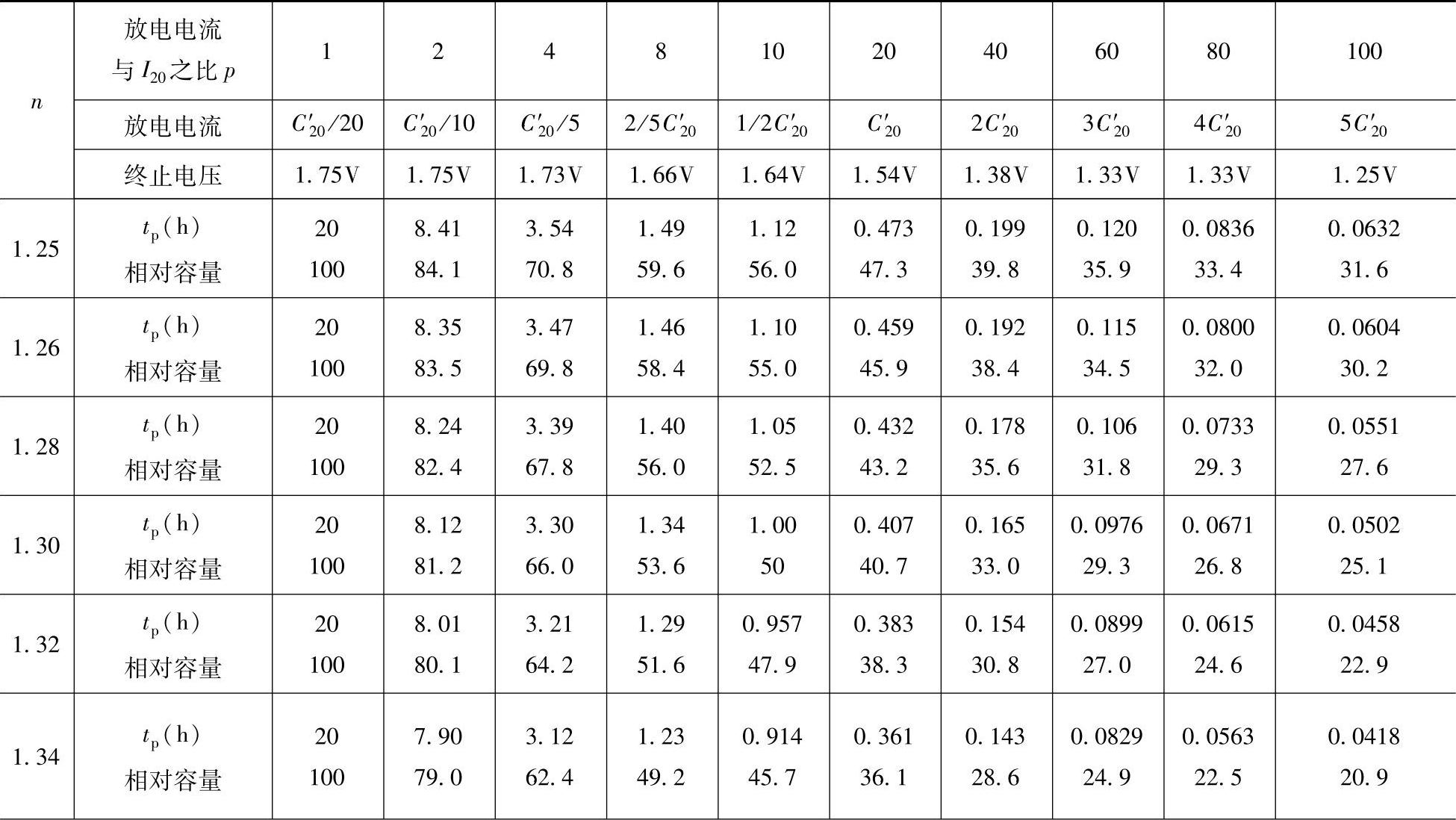
（续）

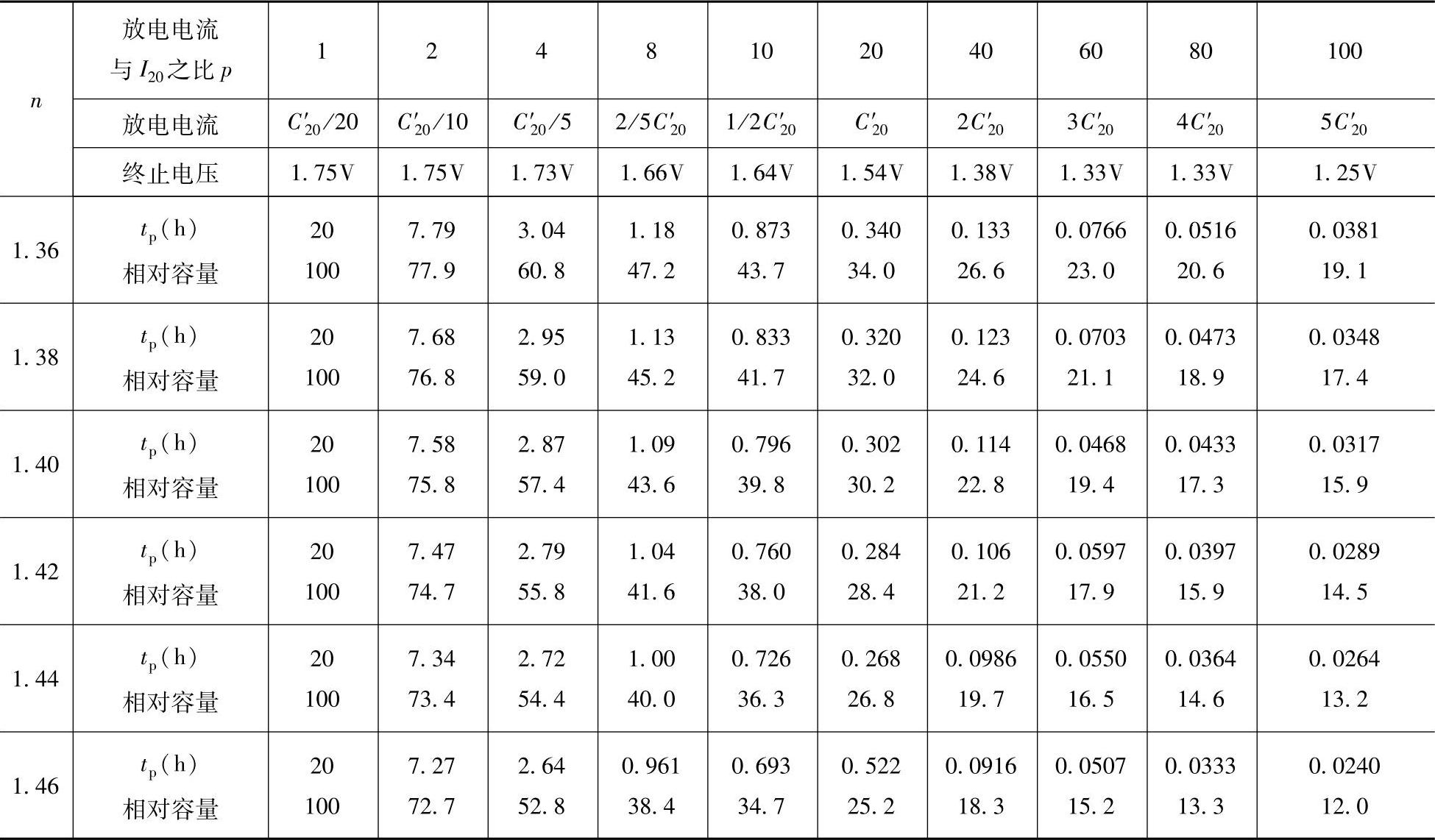
表8-6 六种蓄电池的理论20h率容量C′₂₀

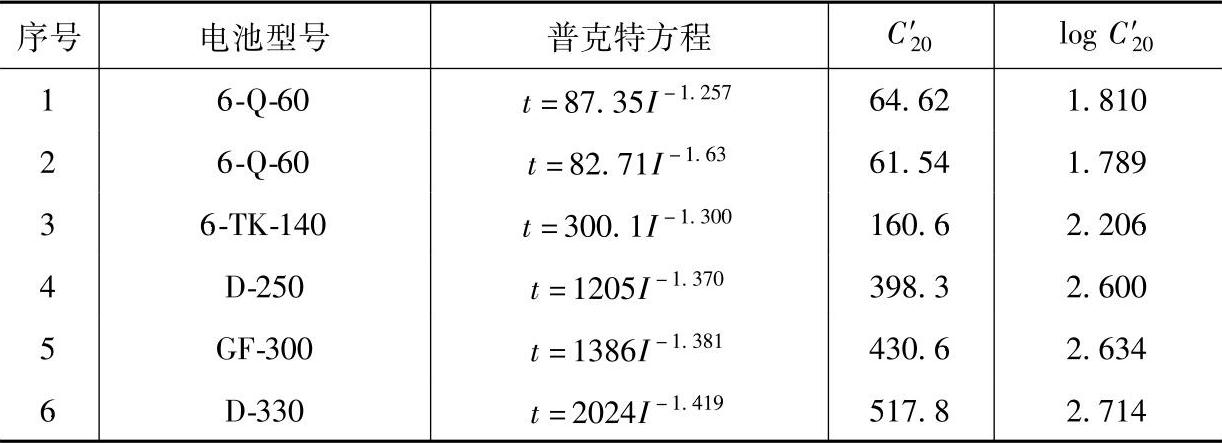
现在来看看另一个常数K。仅从普克特方程的数学表达式看，K是放电电流为1A时的放电时间值。就同一类型的蓄电池而言，K值和理论20h率容量C′₂₀应该是单调一致的。即C′₂₀值大，K值也大；C′₂₀值小，K值也小。用同一种极板装配的同一类型的蓄电池，仅仅是因为单体蓄电池中极板片数不同而额定容量不同，其K值应与蓄电池的C′₂₀成正比，和额定容量也应接近正比关系。对于正极板厚度约为2mm的起动用蓄电池，K值约为其理论20h率容量C′₂₀的1.3～1.4倍，即

K≈1.35C′₂₀（8-17）对于正极板厚度接近5mm的涂膏式蓄电池，其K值约为其C′₂₀的4倍。

对于不同类型不同厚度涂膏式正极板蓄电池，其K值的变化规律较复杂。按式

logK=1.46logC′₂₀-0.70（8-18）计算，得到表8-1中六种蓄电池的logK的计算值与前述根据实验数据依照普克特方程得到的logK值（称为实验值）列在表8-7中。

普克特方程在低放电电流下不适用。因为当I→0时，方程中放电时间（或容量C）的值将近趋于∞。在这种情况下，李宾诺夫（Liebenov）方程^【7】与实验更符合

式中，A和B分别为常数，如果B远大于1，就可以由此得出A和B的物理意义，在这种情况下，C=A/B，即这两个常数之比等于该蓄电池的最大容量。A和B是在很低的放电电流下测定的。

表8-7 不同类型的蓄电池的logK的实验值与计算值

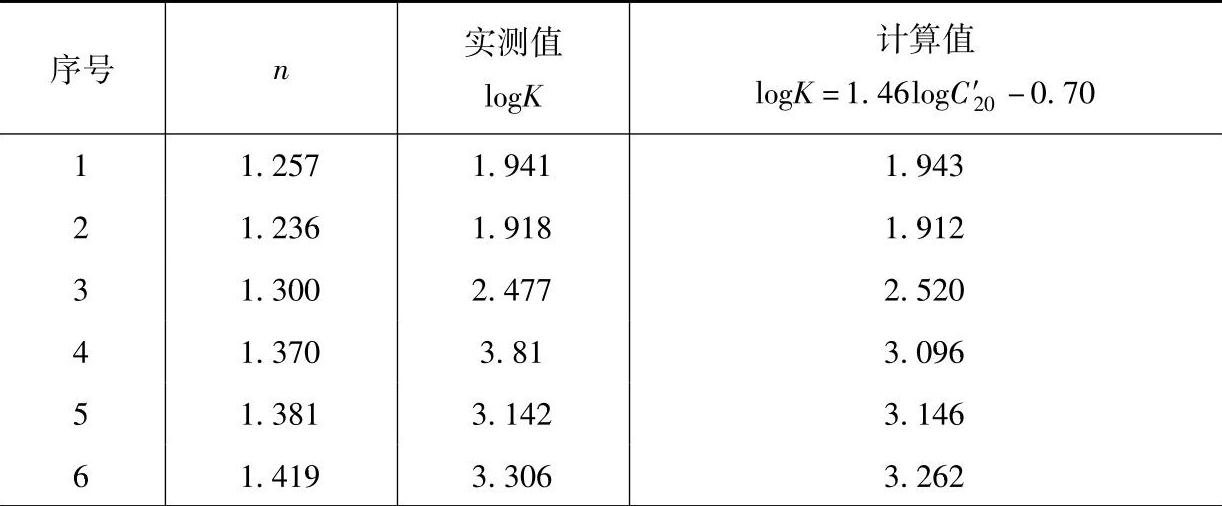
不同温度下蓄电池的容量与放电电流的关系表示在图8-2中。所用的蓄电池的容量为100A·h，内阻约为1.5mΩ。

IEC（International Electrochemical Commission）提出，在30℃以内，t℃时的容量C_t与30℃时的容量C₃₀的关系由下式确定：

C_t=[1+0.008（t-30）]（8-20）

对蓄电池容量与放电条件（温度、电解液浓度等）的关系，有作者做过论述^【8】。

间断放电条件下蓄电池的容量比连续放电时高。间断放电（intermittent discharge）可以不断地缓解电极的极化并降低电池槽上部与极群之间以及极群内部由扩散和对流所产生的硫酸溶液的浓度梯度。图8-3和图8-4表示在27℃时和在0℃时的间断和连续放电条件下100A·h的牵引用蓄电池的放电容量^【9】。

图8-2 不同温度下蓄电池容量对于放电电流密度的依赖关系

E_i—放电初始电压 E_a—放电平均电压 E_e—放电终止电压

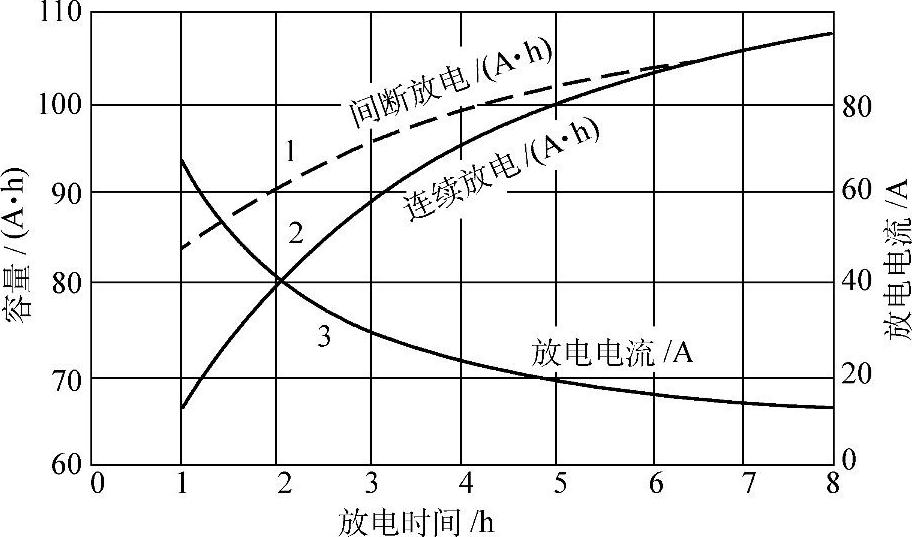
图8-3 100A·h牵引用蓄电池在间断和连续放电条件下，不同放电电流时的容量（27℃）

1—间断放电容量（A·h） 2—连续放电容量（A·h） 3—放电电流（A）

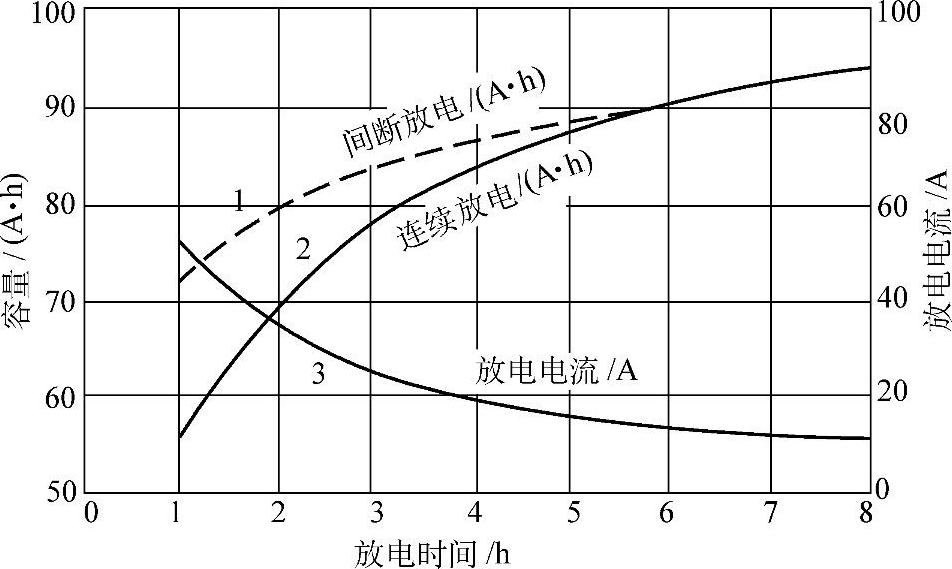
图8-4 100A·h牵引用蓄电池在间断和连续放电条件下，不同放电电流时的容量（0℃）

1—间断放电容量（A·h） 2—连续放电容量（A·h） 3—放电电流（A）

下面谈谈起动用铅酸蓄电池的储备容量问题。

20世纪末，一些国家关于起动用铅酸蓄电池的技术标准和国际电工委员会的技术标准IEC 95-1（5）相继采用储备容量（reserve capacity）的技术要求。储备容量是指蓄电池在一定的温度范围，以25A恒流放电至规定的终止电压，放电持续时间的分钟数。关于储备容量C_r与20h率容量C₂₀的关系，IEC 95-1（5）和中国国家标准GB5008.1—1991给出相同的式子

C₂₀=-133.3+（17778+208.3C_r）1/2（8-21）标准中注明，此式当C_r≥480min（C₂₀≥200A·h）时不适用。式（8-21）可以变换为

C_r=1/208.3（C²₂₀+266.6C₂₀） （8-22）

前面已提到，如果蓄电池的放电电流是20h率放电电流的p倍，那么，根据普克特方程得到的放电时间t_p的表达式即式（8-16）是

t_p=20/pⁿ储备容量规定的25A对于不同容量的蓄电池，其p值是不同的

25=pC₂₀/20即p=500/C₂₀ （8-23）显然，对于容量小的蓄电池，p值大；对于容量大的，p值小。把式（8-23）代入式（8-16）并把t_p（h）变成储备容量C_r（min），得到

C_r=1200·（C₂₀/500）n（8-24）

由式（8-21）或式（8-22）可知，当C₂₀=60A·h时，C_r=94min，由此根据式（8-24）求出n=1.20。即式（8-24）变为

C_r=0.692C₂¹0.20（8-25）

把一系列不同C₂₀值的蓄电池根据式（8-22）（即IEC 95-1）和式（8-25）（即普克特方程）分别计算出来的C_r值（分别称为IEC95-1法和普克特方程法）列在表8-8中。

对于n=1.20的60～90A·h的蓄电池，两种方法计算出来的储备容量C_r的值是一致的或者很接近。随着容量的增大，IEC95-1标准公式的C_r值逐渐偏离式（8-16）（普克特方程）的C_r值。也就是说，大容量的蓄电池，按20h率容量C₂₀检测合格者，如果按储备容量C_r检测，则可能达不到技术要求。

表8-8 两种计算方法得出的不同容量的蓄电池的储备容量

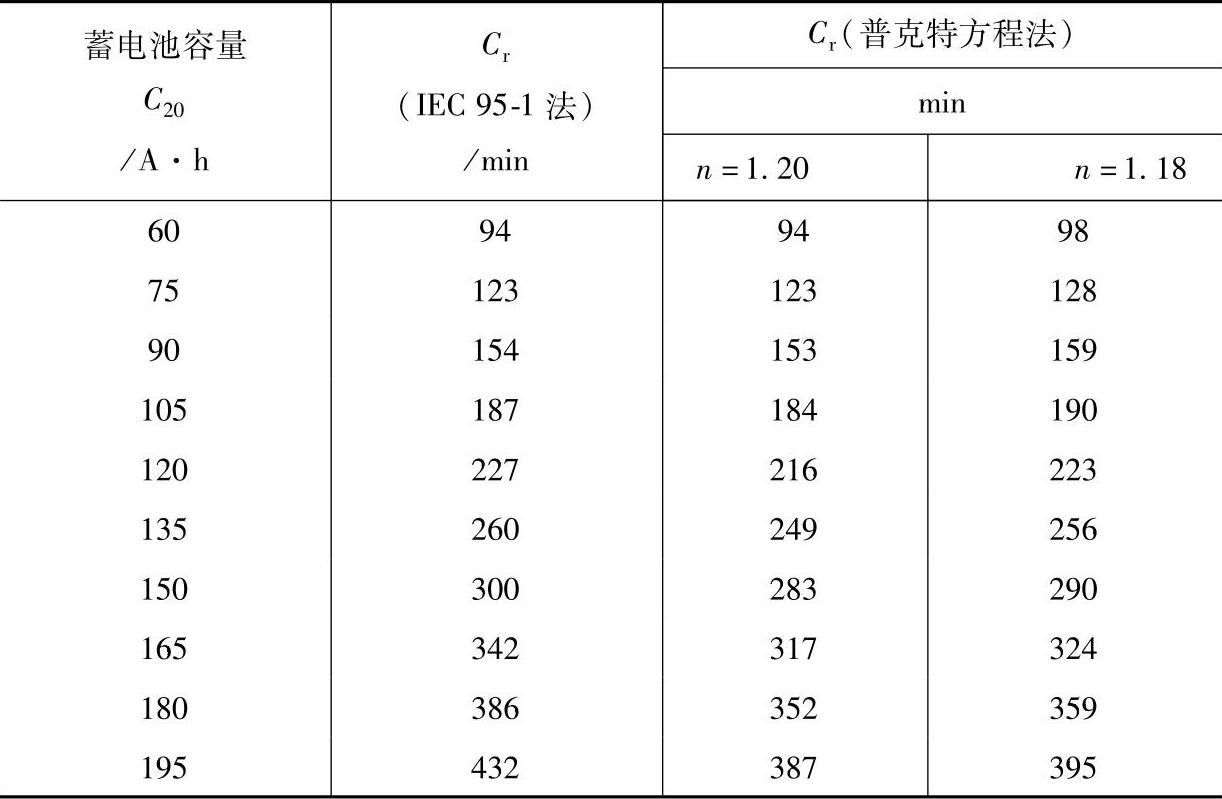
如果蓄电池的n值较小（极板较薄），容量较小（小于60A·h）的蓄电池的C_r两种方法的计算值才会符合一致。随着蓄电池容量增大，二者会出现偏离，但偏离会缓慢些^【10】。

中华人民共和国国家标准GB/T 5008.1—2005《起动用铅酸蓄电池 技术条件》和GB/T 5008.2—2005《起动用铅酸蓄电池产品品种和规格》（以下简称2005标准），关于储备容量与20h率容量之间的换算公式采用了IEC 60095—1∶2000《起动用铅酸蓄电池 第一部分：一般要求和试验方法》的有关内容。储备容量C_r·n与20h率容量C₂₀之间的关系按下式换算

式中，对于富液式免维护蓄电池（排气式蓄电池）

α=1.170，β=0.830，

对于阀控式蓄电池

α=1.130，β=1.070。

这样一来，式（8-26）就变成了

C_r·n=0.830（C₂₀）^1.170（排气式蓄电池） （8-27）

和 C_r·n=1.070（C₂₀）^1.130（阀控式蓄电池） （8-28）

这两个式子和作者1990年从普克特方程出发导出的解析式（8-16）和式（8-25）是同等的^【10】，仅仅是常数略有差异。式（8-26）与普克特方程的一致性，避免了原有的换算公式（8-21）伴随着蓄电池容量变化的偏离。现以60A·h蓄电池为例来讨论。

把我们从普克特方程出发导出的公式（8-16）引来

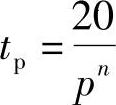
放电时间t_p的单位是h，如果按储备容量记录放电时间如是分钟，就应有一个换算系数60；这里的p是放电电流对于I₂₀（即C₂₀/20）的倍数，储备容量放电电流是25A。这样式（8-16）就可以写成

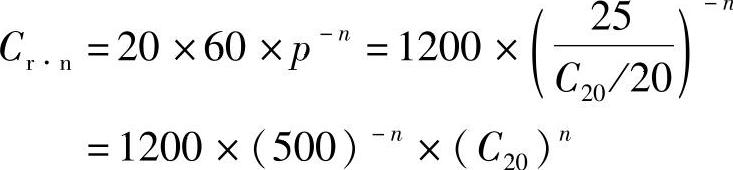
如果取n=1.170（排气式蓄电池），上式变为

C_r·n=0.8344（C₂₀）^1.170 （8-29）

我们从普克特方程出发得到的公式与2005标准给出的换算公式（8-27）形式完全相同，常数也几乎完全相同。可以肯定，换算公式和普克特公式是等同的。

如果取n=1.130（阀控式蓄电池），则得到

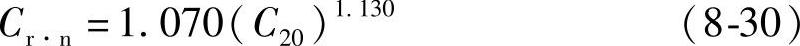
这和2005标准给出的换算公式（8-28）从形式到常数完全相同。可以肯定，换算公式源于普克特方程。

由以上讨论不难看出换算公式中的两个常数α和β的物理意义。α就是普克特方程中的常数n。β是储备容量放电电流（25h）、20h率放电电流（C_20/20A）、放电时间（20h）、小时与分钟的换算系数（1h=60min）与另一常数n之间运算得出的一个常数。这一常数不是独立的，它依赖于普克特方程中的常数n。

用我们从普克特方程导出的式（8-29）计算195A·h蓄电池的储备容量，得到

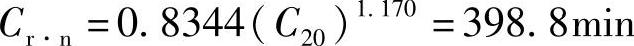
用2005标准中的换算式得到的结果为397min，偏离普克特方程很少。当然，对于阀控式电池的计算式，2005标准与普克特方程是完全一致的。

为了看清常数α（即普克特方程中的常数n）的意义和它与蓄电池性能的关系，再回来看式（8-3），即

K=tIⁿ如果n=1，放电电流I与放电时间t的乘积将是定值，两者是反比关系，即蓄电池的容量是定值，放电电流强度的大小并不影响容量。实际上放电电流大，容量就小。这就是n值的影响。n值越大，这一影响越大。随着蓄电池工艺技术和产品设计的不断进步，n值已由最早约1.4下降至20世纪70～80年代的1.2左右。不仅极板的厚度，还有产品设计的其他参数，如装配的松紧程度也影响n值大小。2005标准中所取n值的数值与当今铅酸蓄电池的水平是相适应的。大电流放电与小电流放电容量的差异较上个世纪已有缩小。