电化学理论基础与快速充电

在不析出氢气和氧气的电位下对蓄电池充电或者化成极板，对于环境保护和节约能源固然是有利的，但所耗时间太长，不能满足生产的需要，会使生产周期不适当的延长。实际上工厂的化成工序和蓄电池充电都采用较大的电流密度，由于阳极极化和阴极极化，正极电位远高于、负极电位远低于各自的平衡电极电位，化成或充电时的端电压U服从于下式：

U=φ₊-φ_-+Ir （7-168）式中，φ₊和φ_-分别是有电流I流过时的正、负极的电极电位，而

φ₊-φ_->E （7-169）E是蓄电池的电动势（两极平衡电极电位之差）。

在较高的端电压下化成或充电，由于正极电极电位较高，负极电极电位较低，在两极分别析出氧气和氢气是不可避免的：在正极

在负极这就使一部分电能消耗于电解水的反应。析出的气体在逸出液面时带出酸雾，污染环境；气体对蓄电池极板和隔板有不同程度的损害。

20世纪70年代开展的快速充电研究取得了不少进展。快速充电的一般方法是用大电流密度化成或充电，但每隔一定时间间隔，给正极瞬时加上负电荷，使其电位迅速降低；给负极瞬时加上正电荷，使其电位迅速升高。这样就降低了充电端电压，抑制了气体的析出。在以后的一段时间里电流的绝大部分都用于蓄电池的充电反应。

脉冲大电流充电的原理，就是利用和充电电流相反的瞬时脉冲电流降低充电时两极的极化过电位（的绝对值），把析出气体的副反应的速率降至最低，使大电流密度能够最大限度地用于充电的电化学反应，以求达到快速充电的目的。

1967年，马斯（J.A.Mas）在第二届国际电动车辆会议上提出快速充电的三定律。

先要明确充电接受电流（charge acceptance current）及其特性。在给蓄电池充电时，如果充电电流低于某一数值，就没有气体产生；只有充电电流达到某一数值时才有微量气体产生。这一充电电流值就叫做蓄电池的充电接受电流。实验证明，蓄电池的充电接受电流I（A）是充电时间t（h）的指数函数

I=I₀e^-at （7-172）式中，a和I₀分别为常数。充电时间从零到t₁，充入蓄电池的电量为C₁（A·h），则

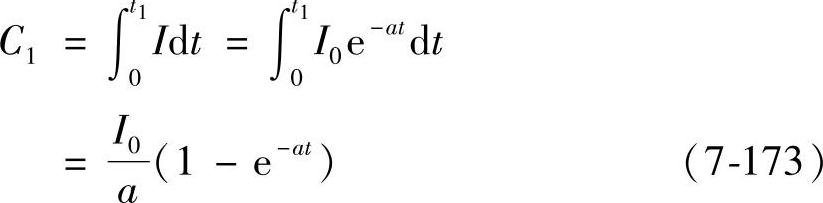
用C表示蓄电池在上次工作中放出的电量。如果蓄电池是在正常工作条件下放出了额定容量，可以视C为蓄电池的额定容量。

图7-14表明了充电接受电流与充电时间的关系。曲线下面的面积表示的是充入的电量。由式（7-173）可知，当t₁→∞时，e^-at→0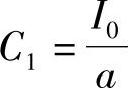，；但此时应有C₁=C。所以有

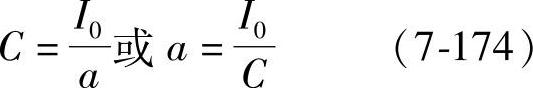
这说明式（7-172）中的两个常数不是彼此独立的。式（7-173）可以写成

C₁=C（1-e^-at） （7-175）由式（7-174）可以看出，常数a的物理意义是单位容量的充电接受电流。蓄电池充电到一定程度时a的意义是否还是这样呢？假定p（t₁，I₁）是曲线I=I₀e^-at上的任一点（图7-14）。此时已充入电量为C₁，待充电量为C₂=C-C₁，p点也应服从式（7-173）和式（7-174），所以有

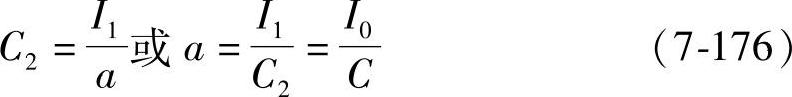
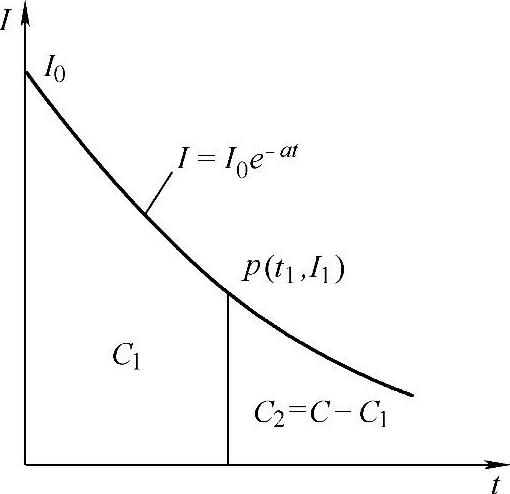
图7-14 铅酸蓄电池的充电接受电流I与充电时间t的关系

蓄电池在充电过程中，其充电接受电流与待充入容量之比是一常数，即单位容量的充电接受电流a。a也叫蓄电池的充电接受率。

如果用电流I=I₀e^-at给一只在上次工作中放出额定容量C的蓄电池充电，在时间t₁充入电量C₁，由式（7-175）可得到

C₁/C可以看成是充电完成程度。

当C₁/C=0.80（充电完成率为80%）时，由式（7-177）求出t₁=1.61/a（h）；当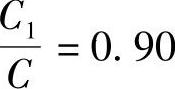（充电完成率为90%）时，求出t₁=2.30/a（h）。当充电完成80%时，充电接受电流大为降低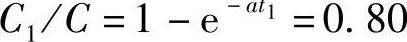：，即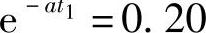此时的充电接受电流为I₁，则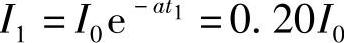，即I₁=0.20I₀I₁仅为I₀的0.20%。同样，在充电完成90%时，充电接受电流I₂=0.10I₀，I₂仅为I₀的10%。可以得出结论，当充电完成率C₁/C=λ时，充电接受电流与原充电接受电流之比为

即I=I₀（1-λ）

充电接受电流I作为充电完成率λ的函数，是一条斜率为-I₀的直线，I随着λ的增大而线性减小。

现在来定量地讨论一下恒流充电的不足之处。

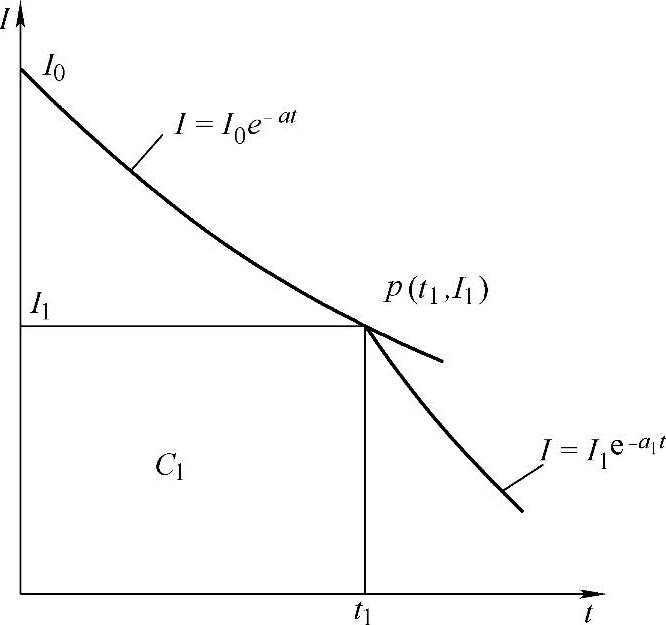
图7-15 铅酸蓄电池的恒流充电与充电接受电流

如果恒流充电的电流大于蓄电池的充电接受电流，多余的电流用于副反应，产生气体。如果恒流充电的电流I₁小于充电接受电流I₀，在时间t₁充入的电量为I₁t₁=C₁（见图7_-15）。继续以I₁充电就会产生气体。这时蓄电池的新的充电接受电流曲线为

当t₁为何值时开始产生气体呢？因为p点在曲线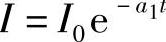上，所以有

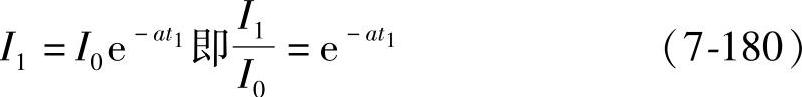
即ln（I₁/I₀）=-at₁，所以t₁=-（1/a）ln（I₁-I₀）（7-181）可知当t₁达到式（7-181）的值时开始产生气体。

以恒流I₁充电至开始产生气体，I₁为何值时所充入容量C₁最大？因为p点在曲线I=I₀e^-at上，所以有

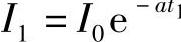
，而

式（7-182）对t₁求导数，得到

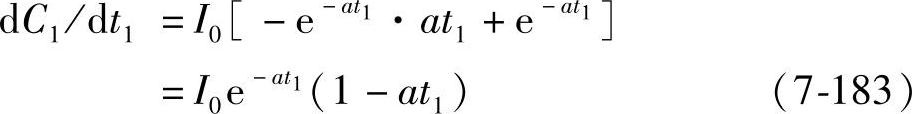
令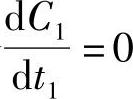，则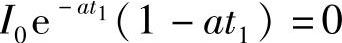得到1-at₁=0所以t₁=1/a（7-184）即当t₁=1/a时，C₁有极大值，此时的充电电流值为

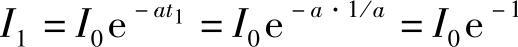
即I₁=I₀/e=0.368I₀(www.xing528.com)

开始产生气体之前的充入电量为C₁=I₁t₁=0.368I₀/a

即C₁=0.368C

可以得出结论，要想在不产生气体的情况下用恒流充电，最多能充入（上次放出电量的）36.8%。

马斯（J.A.Mas）在实验基础上提出的关于蓄电池充电接受电流的规律，所谓马斯三定律可简述如下。

第一定律：对于任何给定的放电电流，蓄电池的充电接受电流I₀与放出电量的平方根C¹/2成正比，即

I₀=KC¹/2 （7-185）

这里K是比例常数。

由式（7-174）可知，I₀=aC，式（7-184）也可以写成

aC=KC¹/2或a=KC^-1/2

式中的K值可由实验求出，其意义可以由下面的运算结果看出。

由I₀=KC¹/2和KC^-1/2=a两式相乘可以得到

K²=aI₀或者-K²=-aI₀ （7-186）而-aI₀正是曲线I=I₀e^-at在t=0处的导数值

dI/dt=I₀e^-at（-a）=-aI₀e^-at

得到[dI/dt]_t=0=-aI₀（7-187）比较式（7-186）和式（7-187）得到

K²=-[dI/dt]_t=0

所以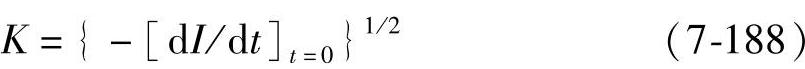

第一定律说明，蓄电池如果以同样大小的电流放电，放出的电量越多，充电接受电流越大。

第二定律：如果蓄电池放出的电量C是给定的，蓄电池的充电接受电流还正比于放电电流I_d的倍数的对数，即

I₀=K₁ C¹/2log（K₂I_d） （7-189）或者引入I₀=aC，把式（7-189）写成

a=K₁ log（K₂I_d）C^-1/2 （7-190）常数K₁和K₂可由实验得出，如一组同样的蓄电池，放出的电量都是C=1A·h，当I_d=10A时，测得I₀=32A（a=32），当I_d=1A时，测得I₀=1A（a=16），将以上这两组数据代入式（7-190）得到联立方程

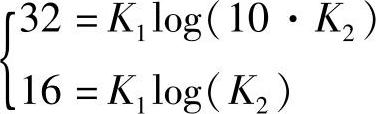
解出K₁=16，K₂=10。将这一组解代入式（7-189），对于这样一组蓄电池来说，第二定律的表达式就是

I₀=16C¹/2log（10I_d） （7-191）

或者 a=16log（10I_d）C^-1/2（7-192）

第三定律：一个蓄电池经几种放电电流放电，其充电接受电流是各个放电电流情况下的充电接受电流之和。即

I_0t=I₀₁+I₀₂+… （7-193）同时服从

式中，I_0t是总充电接受电流；C_t是放出的总电量；a_t是总充电接受率。

由于蓄电池在充电过程中的接受电流不断地按照指数规律下降，如果用恒电流I₀充电，势必产生气体。怎样提高充电接受电流呢？可以用放电的方法。按照马斯定律，蓄电池的充电接受电流，决定于其放电深度（depth of discharge；DOD）和放电电流。采用大电流短时间放电的办法，既不致造成蓄电池容量的显著损失，又可以提高充电接受电流。

例如，蓄电池的充电接受电流和充电时间的关系为

I=I₀e^-at（7-172）

实验得到 I=100e^-10t（7-195）如果采用这样的指数电流来充电，那么充电多长时间，充电接受电流I降至原来的99%，即99A？

式（7-172）变换为I/I₀=e^-at，代入实验数据有99/100=e^-10t，则ln0.99=-10t，得到

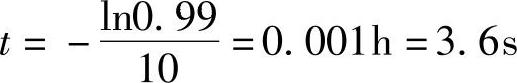
即充电3.6s，充电接受电流降低1%。

如果这时停止充电，并用300A放电，就可以使充电接受电流提高到原来值的100A。那么放电多长时间就可以达到目的呢？

如果蓄电池的有关常数K₁、K₂如前所述，分别为K₁=16，K₂=10，那么就有

这里C_d是放出的电量。按照第三定律，蓄电池的充电接受电流应是原充电接受电流（99A）与这次放电造成的充电接受电流I₁之和。那实际上是要求I₁=1A，即

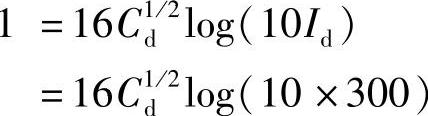
求出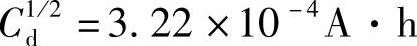而放电时间t_d为

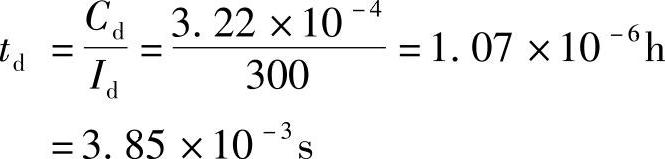
可以看出，放出的电量和放电时间与充入电量和充电时间比较起来都是很少的，但是充电接受电流却恢复到了原值。这就使脉冲大电流充电有了可能。问题的实质是大电流放电降低了极化，降低了过电位，使得在大电流下充电时的端电压不过高，不产生气体。