扩散方程下的浓差极化过电位与电流密度的关系

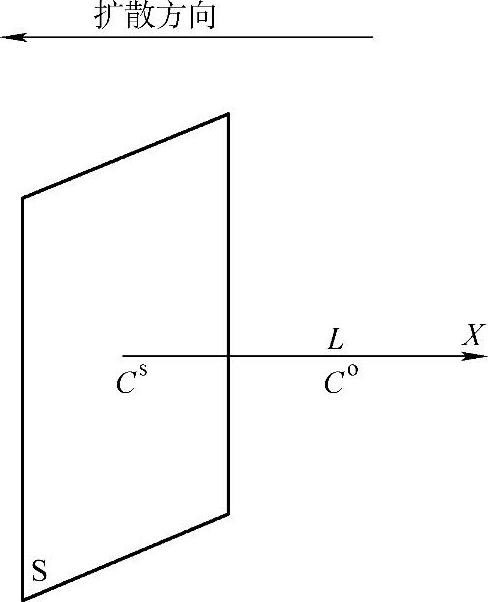
图7-10平面电极稳定扩散示意图

为了讨论浓差极化导致的过电位，必须先确定扩散动力学的最简单的问题——稳定扩散条件下的扩散方程（diffusion equa-tion）。

根据扩散定律（diffusion law），在时间Δt之内，通过一个垂直于x轴（浓度增加方向）的平面的扩散的物质（离子）的量m与浓度梯度（concentration gradi-ent）∂C/∂x、截面积S以及时间区间Δt成正比（图7-10）

m=DS（∂C/∂x）Δt （7-137）式中的比例系数D是扩散系数（diffusion coefficient）。在电极表面附近，式（7-137）可以写成

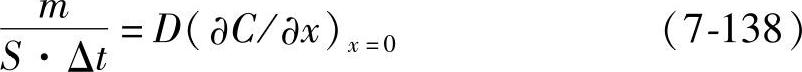
m以mol为单位，通过系统的物质（离子）的摩尔数为n，其所带的电荷为nFm。

式（7-138）可以写成

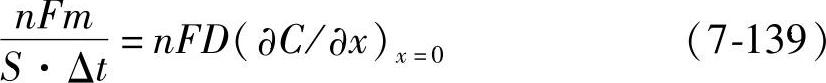
式（7-139）的左边是单位时间内通过单位面积的电量，即电流密度i。式（7-139）变成

如果到电极表面的距离为L的溶液内部的浓度为C^o，电极表面附近的浓度为C^s，在稳定扩散的情况有

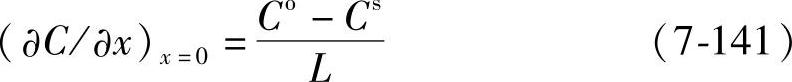
式（7-140）就可以写成

式（7-142）表示流过电极的电流密度与电极表面附近的离子的稳定浓度C^s之间的关系。

当电流密度增加时，电极表面附近的离子浓度应当降低。C^s的数值是可变的，它从电流密度接近于零时的最初浓度值C^o开始，当i增加时，它可以降至零。当C^s=0时，i达到一个极限值i_M。iM叫做极限扩散电流（limiting diffusion current）。

当C^s=0时，式（7-142）变成

现在来讨论浓差极化过电位，把式（7-142）写成

变换为

电极电位和浓度（在这里我们忽略浓度与活度的差别）的关系由式（7-55）表示的能斯特方程决定

把式（7-145）代入式（7-146）得到

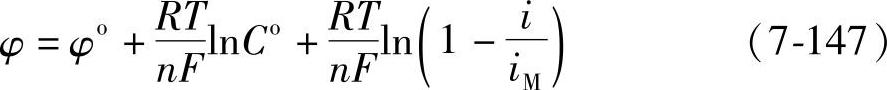(www.xing528.com)

显然，平衡电极电位值是式（7-147）右边的前两项，即φ^o+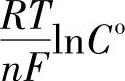，过电位的值是

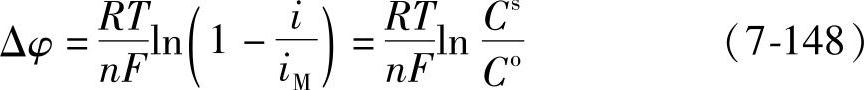
式（7-147）称为浓差极化方程式。它在电流通过电极时，只是由于离子浓度的变化而影响电极电位的条件下表示过电位与电流密度之间的关系。

由式（7-148）可以看到，当i→0时，过电位Δφ→0。当电流密度i增大时，由于决定电极电位的电极表面附近的离子浓度降低，C^s<C^o，电极电位向负的方向移动，即Δφ为负值。这和表7-12所述负极作为阴极时阴极过电位小于零的结论是一致的。

应当指出的是，式（7-148）仅适用于稀溶液。浓溶液中电极电位的公式中的浓度要用活度，浓溶液的扩散系数不是常数而是浓度的函数，问题变得复杂了。还有，式（7-148）是从电极上仅有析出氢的电化学反应的假设得出来的，所以当i→i_M（即C^s→0）时，Δφ→-∞。实际上，当过电位的绝对值增大时，新的电化学过程成为可能，不会出现Δφ→-∞的情况。

在阳极溶解的情况下，过电位Δφ的表达式与式（7-148）有所不同。这种情况下的扩散电流为

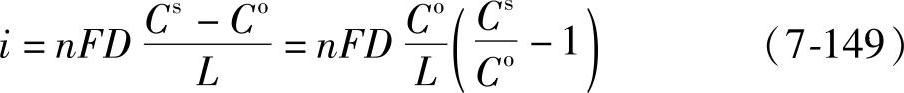
即

式（7-150）变换为

得到的过电位表达式为

由式（7-152）可以看出，阳极过电位Δφ总是大于零，即电极电位向正的方向移动。这和本章第九节中表7-12所述阳极过电位大于零的结论是一致的。

铅酸蓄电池在放电时，浓差极化过电位的情况如何呢？正如式（7-58）和（7-59）所示的，两极的平衡电极电位是

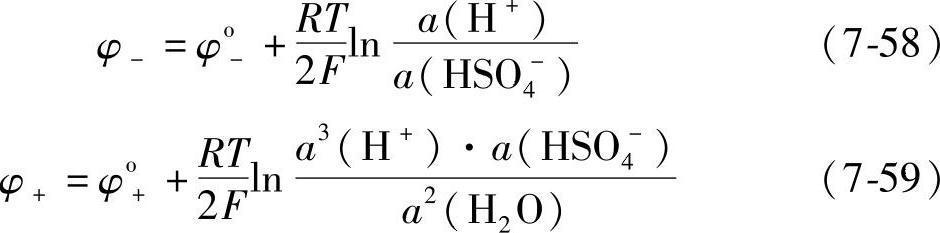
用φ-′和φ+′表示放电时两极的电极电位

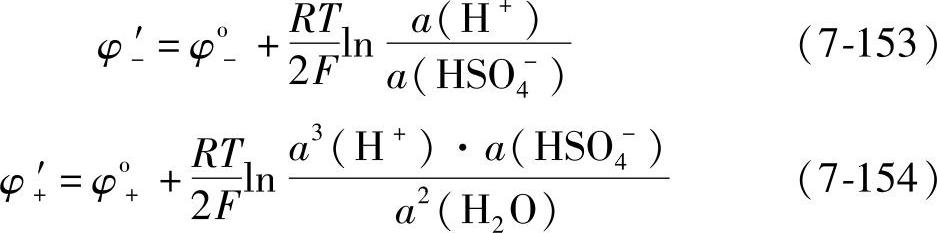
由式（7-1）和式（7-2）表示的铅酸蓄电池放电时的电极反应方程可知，在放电时，在负极（阳极）要消耗HSO₄-离子而生成H^+离子，在正极（阴极）要消耗HSO₄-和H+离子而生成H₂O。为了清楚说明，这里用a′表示放电时各种离子或H₂O的活度，以区别于平衡时的活度a，那么负极（阳极） a′（HSO₄-）<a（HSO₄^-） （7-155）

a′（H⁺）>a（H⁺） （7-156）正极（阴极） a′（H⁺）<a（H⁺） （7-157）

a′（HSO₄^-）<a（HSO₄^-） （7-158）

a′（H₂O）>a（H₂O） （7-159）

由此可知φ′->φ-即Δφ->0 （7-160）

φ′₊<φ₊即Δφ₊<0 （7-161）

蓄电池放电时，浓差极化使正极电极电位降低，使负极电极电位升高。

蓄电池充电时，情况和放电时相反，浓差极化使正极电极电位升高，使负极电极电位降低。