微波S参数的特性分析

1.微波S参数的定义

在较低频率中，一般用阻抗Z参数或导纳Y参数来表述网络特性，这些参数的定义都是基于电压、电流的概念，测量时需要在特定的端口条件下（如开路、短路）测出对应的电压和电流，由此确定各个参数。而高频条件下的电压和电流参数很难测量，而且有时不允许人为地将网络端口开路或短路，因此上述测量方法并不适用于微波频率，必须应用不同的概念，采用不同的方法实现测量。

由于“波”的概念的引入，微波网络常用散射参数（Scattering Parameters，S参数）表示：任何网络都可用多个S参数表征其端口特性，对n端口网络需要n²个S参数。如单端口网络有1个S参数，双端口网络有4个S参数，三端口网络有9个S参数等。以图12-12所示的双端口网络为例，DUT外部的带箭头线用来表示加在其端口上的信号及其流动情况。

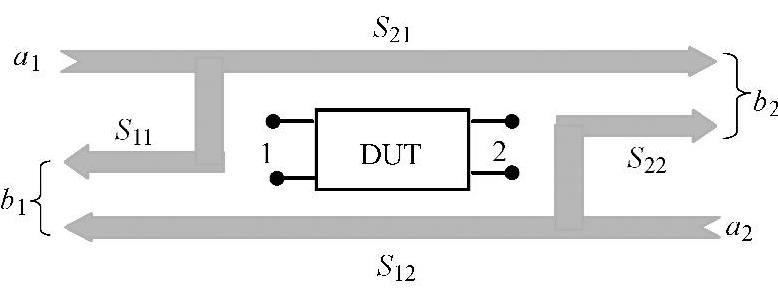
图12-12 微波网络S参数

图中，当入射波a₁进入端口1时，其中一部分会因端口失配而反射回来，大小为S₁₁a₁；a₁其余部分经网络传输到端口2上成为出射波，大小为S₂₁a₁。同样地，若有入射波a₂进入端口2，其中一部分也会因失配反射回来，大小为S₂₂a₂；a₂其余部分经网络传输到端口1上成为出射波，大小为S₁₂a₂。

用b₁、b₂分别表示端口1和端口2上的所有出射波，有

b₁=S₁₁a₁+S₁₂a₂

b₂=S₂₁a₁+S₂₂a₂ （12-4）

式中，S₁₁、S₂₁、S₁₂、S₂₂就是表示双端口网络的四个S参数，被称为散射参量，式（12-4）也由此被称为散射方程组。

四个S参数均有固定的物理意义。用一个匹配负载Z₀终接在端口2上，且当端口2上的入射波a₂=0时，由式（12-4），有

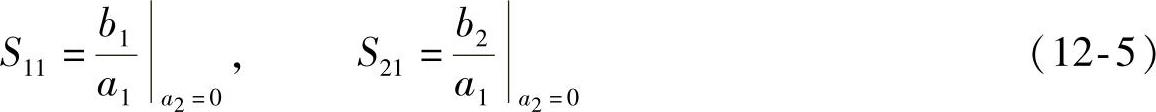
同样地，在端口1终接上匹配负载Z₀，且当端口1上的入射波a₁=0时，有

可见，在S参数的两个数字下标中，如果用第一个代表波出射的端口、第二个代表波入射的端口，则S₁₁是端口2匹配时端口1的反射系数；S₂₂是端口1匹配时端口2的反射系数；S₂₁是端口2匹配时的正向传输系数；S₁₂是端口1匹配时的反向传输系数。所有S参数都是同时包含幅度、相位两种信息的复数值。一般来说，|S₁₁|和|S₂₂|均小于1；对有衰减的器件，|S₂₁|和|S₁₂|均小于1；对有增益的器件，|S₂₁|和|S₁₂|均大于1。

由S参数可以推导出其他网络参数，如电压驻波比、反射系数、阻抗、回波损失等反射参数，以及增益、衰减、传输系数、相移、时延等传输参数。各表达式如下：

（1）反射参数

电压驻波比（二式均可）：，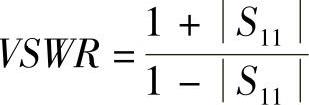

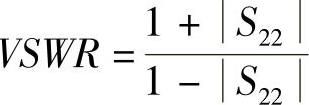
反射系数：端口1上Γ=S₁₁；端口2上Γ=S22

阻抗：端口1上；端口2上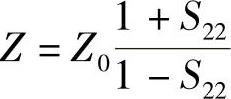

回波损失：端口1上R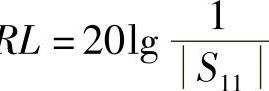；端口2上

（2）传输参数

增益：G=20lg|S₂₁|

衰减：A=-20lg|S₂₁|

传输系数：正向T=S₂₁；反向T=S₁₂

传输相移：正向φ=arctanS₂₁；反向φ=arctanS₁₂(www.xing528.com)

群时延：GD=dφ/dω（ω为角频率）

2.S参数的流图表示及计算

为了简洁而完备地描述网络的全部特征，可以借用信号流图（信流图）的方式。信流图用节点代表信号，用支路和箭头代表信号及其流动的方向，并用支路旁标代表支路的传递函数即信号大小。图12-12所示的双端口网络因此可用信流图表示为图12-13。

图12-13 用信流图表示的双端口网络

类似地，一个三端口网络（如定向耦合器）也可以用信流图表示，如图12-14所示。经由定向耦合器传输的信号通常以端口1到端口2的通路为正向传输通道，端口3为耦合口，与信号的出射口2之间应有隔离。在图12-14所示的9个S参数中，S₂₁、S₁₂分别是端口1和端口2之间的正、反向传输系数，S₃₁、S₁₃是端口1和端口3之间的耦合系数，S₂₃、S₃₂是端口2和端口3之间的隔离系数，S₁₁、S₂₂、S₃₃分别是三个端口上的反射系数。

定向耦合器的一项重要指标是等效方向性（Directivity），定义为D=S₃₂/S₃₁，表示正向、反向传输时在耦合端口3上的信号差别。理想的定向耦合器应满足下列各式：S₁₁=S₂₂=S₃₃=0，S₃₂=S₂₃=0，S31=S13=常数，D=0。但在实际应用中，不一定全部满足。

将信流图简单、直观的表示方法与梅森（Mason，或译作梅逊）法则相结合，会使它在分析和计算组合网络特性时更加方便。Mason不接触环路法则可用下式表述

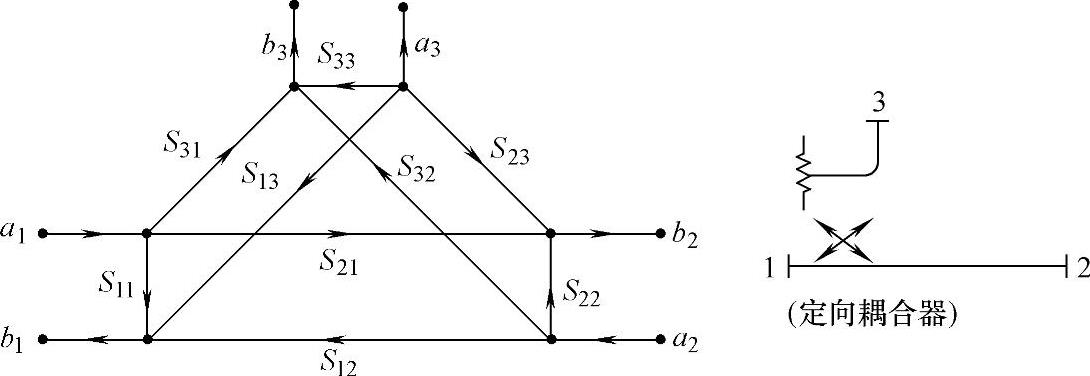
图12-14 用信流图表示三端口网络

式中，T表示信流图所代表的网络的增益或传输函数；T_k是从输入到输出的第k条路径上所有支路旁标（系数）的乘积；Δ是信流图的行列式，即信流图所代表的网络的联立方程组的行列式，计算式为Δ=1-∑L_k¹+∑L²_k-∑L³_k+…（∑L_k¹表示信流图中全部环路的增益之和；∑L²_k表示所有两两不接触环路的增益乘积之和；而∑L³_k则表示所有可能的三个互不接触环路的增益乘积之和……依次类推）；Δ_k是与第k条开路不接触的子信流图的行列式。

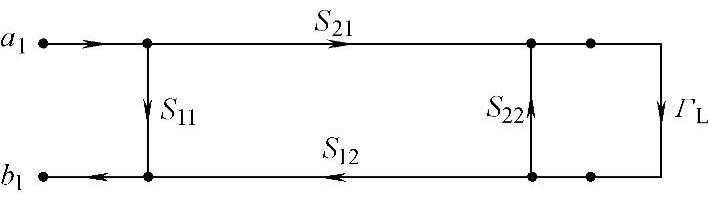
图12-15 终接负载的双端口网络信流图

Mason不接触环路法则的应用举例如下：在双端口网络的端口2上终接一个反射系数为Γ_L的负载，网络信流图如图12-15所示。应用Mason法则，有

Δ=1-S₂₂Γ_L （全图只有一个环路）

T₁=S₁₁，Δ1=1-S₂₂Γ_L （从a₁输入到b₁输出的第一条路径）

T₂=S₂₁S₁₂Γ_L，Δ2=1 （从a₁输入到b₁输出的第二条路径）

故有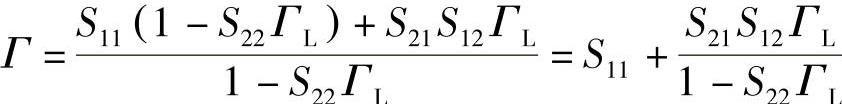

归纳起来，在微波频率段应用S参数具有以下优点：

1）微波网络一般有明确的特性阻抗，S参数特别适于分析特性阻抗为50Ω的微波网络或系统。

2）S参数在微波网络中有明确的物理意义且便于使用。传输参数代表复数的插入损耗或插入增益，反射参数代表网络与源或负载之间的失配情况。

3）S参数便于实际测量。当信号源内阻和负载阻抗均为理想的50Ω特性阻抗时（达到匹配条件），通过反射和传输测量即可获得网络的S参数。即便出现源失配和负载失配，现代矢量网络分析仪也可以通过误差修正将失配的影响降低到可以忽略的程度。

4）S参数便于电路设计和计算分析，而且采用S参数表征网络特性最适于用信流图来解决复杂的微波网络问题。