提高频率分辨力的锁相合成技术优化

在图9-21b所示的数字倍频环中采用可变分频器，就可以从单个基准频率获得一系列频率，环路中的分频器如果采用可编程分频器来改变分频比N，输出频率f_o=Nf_i，就可以按增量f_i来改变。当需要进一步提高锁相环的输出频率的上限和频率的分辨力时，这种基本锁相环存在两个问题。首先，由于可编程分频器的最高工作频率比固定分频器的最高工作频率低很多，将VCO的输出直接加到程控分频器上就限制了频率合成器输出频率的上限。另一个问题是输出频率以增量f_i变化，即合成器的频率分辨力等于f_i。若要提高分辨力，要求增量要小，则要求f_i越低，锁相环的转换时间越长（转换时间t_e一般可用经验公式t_e=（25/f_i）来计算）。分辨力高与转换时间短的要求相矛盾。下面将讨论如何解决上述两个问题。本节首先讨论提高环路分辨力的问题，下节再讨论扩展输出频率上限的问题。

提高锁相环的频率分辨力，可以采用微差混频、多环频率合成及小数分频等方法。

1.微差混频法

微差混频法是将两个频率相差甚微的信号进行差频混频，如图9-25所示。

在图9-25a中，混频器的输出频率为

f_o=Nf_i1-Nf_i2=N（f_i1-f_i2）=NΔf （9-15）

在图9-25b中，VCO的输出频率为

图9-25 微差混频原理

a）倍频—混频式 b）混频—倍频式

f_o=N（f_i1-f_i2）=NΔf （9-16）

由式（9-15）和式（9-16）可见，图9-25所示的两种方法的输出频率分辨力是Δf。在微差混频法中，由于参与混频的两个信号频率十分接近，Δf很小，使分辨力得到提高。但是，在图9-25a中，当这两个频率很接近时，在混频器工作中将会发生严重的频率牵引现象，这一问题在实际中很难解决，其应用受到局限。

2.后置分频法

提高频率分辨力的途径之一如图9-26所示，在锁相环后设置一分频器，则输出频率fo=（N/M）f_i，当N改变1时，f_o变化量为f_i/M，因此在不增加转换时间的前提下使分辨力提高为原来的M倍，但相应地输出频率范围也缩减为原来的1/M。

图9-26 后置分频器的PLL合成器

为了在提高频率分辨力的同时，输出频率范围不发生变化，可以采用基于后置分频的多环频率合成方法，图9-27是一个三环锁相率合成器原理框图。

图9-27 三环PLL合成器

a）组成原理图 b）简化框图

环A、环B是两个倍频环，均以f_i为参考输入频率，环B的输出f_B经过M后置分频后作为环C的参考输入频率，环C的输出频率f_o与环A的输出频率f_A混频后作为环C的反馈。由图9-27可知，环A和环B的输出频率分别为

f_B=N_Bf_i （9-17）

f_A=N_Af_i （9-18）(www.xing528.com)

由环C锁定时有

因此，合成器的输出频率为

当N_B改变1时，输出频率f_o变化量为（1/M）f_i，故其频率分辨力可达（1/M）f_i，而转换时间由三个环共同决定，A、B环参考频率为f_i，C环参考频率为f_B/M，若取N_B比M大，则（f_B/M）>f_i，则整个环的转换时间仍为t_e=25/f_i。因此在提高频率分辨力的同时，其转换时间并未加长。

3.小数分频技术

（1）小数分频原理

实际中的数字分频器总是整数分频，其分频系数都是整数。所谓小数分频是通过分频比可变的整数分频，经多次平均的办法，从宏观上实现小数分频，即小数分频只是一种平均的效果。具体地讲，若希望分频系数有整数部分也有小数部分，即分频系数为N.F，其中整数部分为N，小数部分为F，小数部分的位数为n。欲获得其值界于N和N+1之间的小数分频，可让整数分频系数在N和N+1两个值中改变，其办法是在总的分次数为10ⁿ次的一个循环中，进行F次（N+1）分频，（10ⁿ-F）次N分频，则在一个循环内分频系数的平均值为

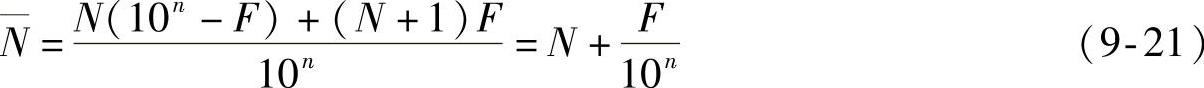
即实现了小数分频。例如，要实现4.3的小数分频，对应式（9-21），N=4、n=1、F=3，只要在10次分频中作7（=10-3）次除4，3次除5，则得到：。

（2）分频比“掺匀”控制

既然小数分频器中存在N及（N+1）两种分频，而且每种分频都可能进行很多次，两种分频的次数不仅要准确地控制，并且还应该设法把两种分频混合均匀，而不要集中在一段时间内都做N分频，而在另一段时间都做（N+1）分频，以免对应的输出频率不均匀。

这种分频比“掺匀”的控制可以通过累加运算来完成。具体做法是对小数部分F进行累加计数，若每一次累加结果未产生高位溢出（未达到整数1）时，则进行N分频；若累加结果产生高位溢出时，则进行（N+1）分频。经过10ⁿ累加计数，累加值回零，又重复一次新的累加循环。这样，在一个累加循环过程中，能自动控制N分频做（10ⁿ-F）次，（N+1）分频做F次，而且把N与（N+1）两种分频也自动“掺匀”了。

下面用一个实例来说明上述过程。例如，按上述方法进行4.3次分频的控制，一个循环中的10次累加过程见表9-1。由表9-1可见，在对小数部分0.3进行累加的过程中，未发生高位溢出时进行4分频，发生高位溢出时进行5分频。在一个循环的10次分频中，4分频做了（10-3）=7次，5分频做了3次。而且做4分频和5分频的操作，是被自动“掺匀”后穿插进行的。

表9-1 小数分频的工作过程（分频比为4.3）

为了进一步提高合成器的频率分辨力，可扩展小数部分F的位数。小数部分的位数越多，频率分辨力越高。例如，把F扩展为两位，要实现4.36次小数分频，只要在每100（作10²）次分频中，作（100-36）=64次除以4，36次除以5，即可得N=（64×4+36×5）/100=4.36。

（3）基于小数分频的锁相环电路

基于小数分频的锁相倍频环原理图如图9-28所示。图中的锁相环路部分与普通的锁相倍频环基本上相同，其主要差别是在÷N分频器之前增加了脉冲删除电路，其作用是在删除控制信号的作用下，可从VCO返回的脉冲信号序列中删除一个脉冲。图9-28中小数值以BCD码写入F寄存器，在输入基准频率f_r的作用下，F寄存器的存数与相位累加器的存数在BCD加法器（ACCU）中相加。当BCD加法器达到满度值时就产生溢出，溢出脉冲（OVF）作为删除控制信号加到脉冲删除电路，删除一个来自压控振荡器的脉冲，使÷N分频电路少计一个脉冲（见删除电路输出波形图），相当于分频系数为（N+1）；在溢出的同时，加法器将本次运算的余数存入相位累加器；如果在f_r作用下加法器相加结果达不到满度值，则不会产生溢出，锁相器仍按照÷N进行分频，并且本次相加的结果存入累加器，作为加法器的基数，等待下一次相加，如此重复进行。

图9-28 基于小数分频的倍频环原理图

小数分频面临的最大问题是如何补偿由于脉冲删除所引起的锁相环相位抖动。例如用表9-1所示的实例构成一个基于小数分频的锁相倍频环，VCO输出频率f_o=4.3f_i，每经输入频率f_i的一个周期，VCO的输出频率f_o为4.3个周期，在第1个参考周期之后，鉴相器输入端就出现了0.3×360°的相位误差，在第2个周期后相位误差变为0.6×360°，第3个周期后相位误差变为0.9×360°，第4个周期后相位误差累计超过360°，余下0.2×360°的相差。相位变化累积达360°时，多出一个信号周期，为了实现小数分频，必须把VCO的输出删除一个信号周期。显然，删除操作会出现相位突变，经÷N分频器的反馈信号的相位突然滞后输入信号一个相位。这样，使得鉴相器的输出电压出现阶梯形变化（见图9-28）。

为了补偿在工作过程中鉴相器输出电压的阶梯形变化，可采用相位内插补偿措施。从表9-1可见，累加值（累加器中的存数）恰好也是一个阶梯变化，因此将该数据送入DAC，用其阶梯输出去补偿鉴相器输出的阶梯形变化，即两者相减后减法器输出到LPF，环路稳定后经环路LPF送给VCO的则是一个较平稳的直流电平。在一定程度上，消除了VCO输出频率的相位突跳。