如何评价测量系统动态特性？-测量系统动态特性评估指标探析

测量系统的动态特性可用动态性能指标进行评价。为了便于比较，可采用两种方法：①采用阶跃信号作为系统输入量，获得系统对阶跃响应的过渡过程曲线与在时域中描述系统动态特性的指标；②采用正弦信号作为系统输入量，获得系统的频率响应特性与在频域中描述系统动态特性的指标。

1.评价系统动态特性的指标

（1）评价系统动态特性的时域指标

1）时间常数τ。一阶系统中定义单位阶跃响应（曲线）由零上升到稳态值的63.2%所需要的时间为时间常数τ。τ越小，响应速度越快，系统的动态特性越好。

2）上升时间t_r。上升时间是指输出指示值从最终稳定值的5%或10%变到最终稳定值的95%或90%所需要的时间。

3）响应时间t_s。响应时间是指从输入量开始起作用到输出指示值进入稳定值所规定的范围（稳定值的95%或98%，这时允许误差为±5%或±2%）所需要的时间。

4）超调量δ。超调量是指输出第一次达到稳态值后又超出稳定值而出现的最大偏差值，常用最终稳定值的百分比表示。

（2）评价系统动态特性的频域指标

评价系统频域动态特性时，常用幅频特性与相频特性，一般希望幅频特性平直段长，相频特性的相位差φ（ω）与频率ω成线性关系，其指标是频带宽度，简称带宽。带宽是指幅频特性误差为±5%或±2%（或其他规定）的频率范围。对于对数幅频特性，带宽是指增益变化不超过某一规定分贝值的频率范围，一般规定为对数幅频特性曲线上衰减为3dB以内。对相位还有要求的系统，应对相频特性提出要求。例如在工作频带范围内，相角应小于5°或2°或其他规定的值。

这样，一般用带宽、带宽内幅值误差以及带宽内相位差等指标来比较完整地评价系统的动态特性。

2.测量系统的动态性能指标的测定

每一种测量系统组建成功之后，都要进行一系列实验，测定该系统的性能指标。下面介绍动态特性指标的实验测量方法。

（1）时域测定法

时域法一般是通过测量测试系统对单位阶跃信号的响应来确定其动态特性参数。

1）一阶系统。以单位阶跃激励一阶测试系统，得到系统对单位阶跃的响应，取输出值达到最终值（稳定值）的63.2%时所经历的时间作为时间常数τ。但是这样由单个测试点获得的瞬时值来确定的τ值，准确性较差。

采用观测响应全过程的方法来确定时间常数τ，可获得更可靠的结果。一阶系统的单位阶跃响应为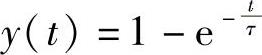

或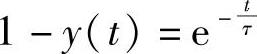

两边取对数，有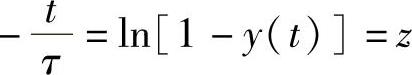

上式表明，ln[1-y（t）]与t成线性关系。因此测得各时刻t对应的y（t）值，再作出ln[1-y（t）]-t曲线，如图8-20所示。根据曲线的斜率值确定时间常数τ，即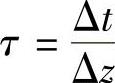，显然，这种方法考虑了阶跃响应全过程，运用测试数据来决定τ，结果比较准确。

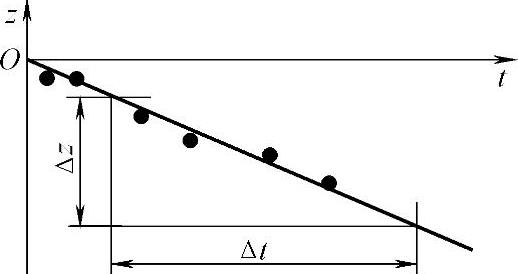
图8-20 求一阶系统时间常数

2）二阶系统。典型的欠阻尼二阶系统的单位阶跃响应函数（见式（8-77））表明，其阶跃响应是一个以角频率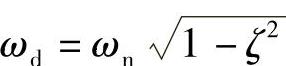（欠阻尼固有角频率）作衰减振荡的函数，如图8-21所示。按照求极值的通用方法可求得各振荡峰值所对应的时间t=0，π/ω_d，2π/ω_d，…。将t=π/ω_d代入式（8-77）中，求得最大超调量M和阻尼比ζ的关系式（见图8-22）为

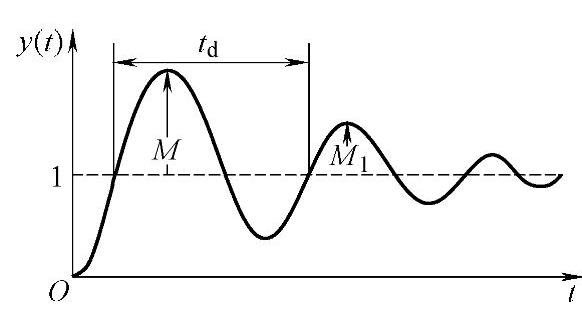
图8-21 二阶系统（ζ<1）的阶跃响应

(www.xing528.com)

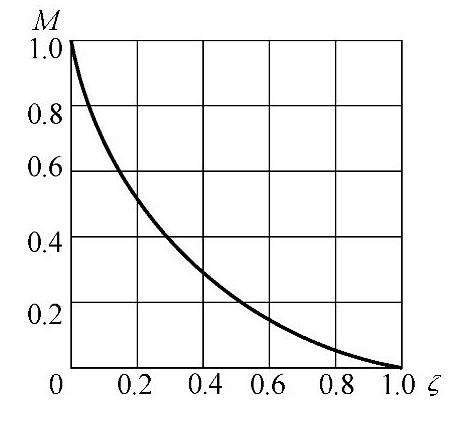
图8-22 ζ-M的关系

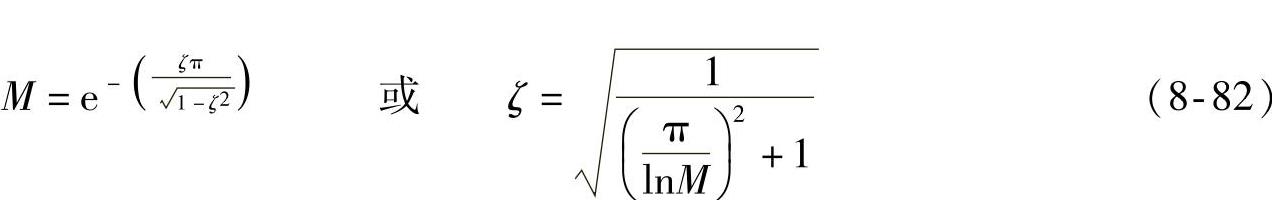
因此，测得M之后，便可按式（8-82）或者与之相应的图8-22来求阻尼比ζ。

如果测得阶跃响应有较长的过渡过程曲线，可利用任意两个超调量M_i和M_i+n来求阻尼比ζ，这样确定的ζ比较准确，其中n为该两个峰值相隔的周期数（整数）。设M_i峰值对应的时间为t_i，则M_i+n峰值对应的时间为

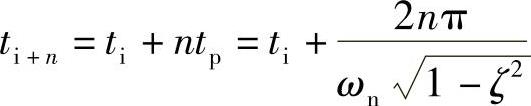
将它们代入式（8-77）可得

整理后得

式中，。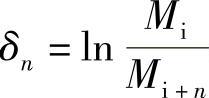

当ζ<0.1时，以1代替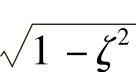不会产生过大的误差（不大于0.6%），则式（8-83）可改写为

若系统是线性的二阶系统，那么n值采用任意正整数所得的ζ值不会有差别。反之，若n取不同值，则获得不同的ζ值，这表明该系统不是线性二阶系统。

（2）频域测定法

利用正弦激励，可以得到系统的幅频特性，如图8-23和图8-24所示，然后根据这两个特性曲线求得一阶系统时间常数τ、二阶系统的固有频率ω_n和阻尼比ζ。

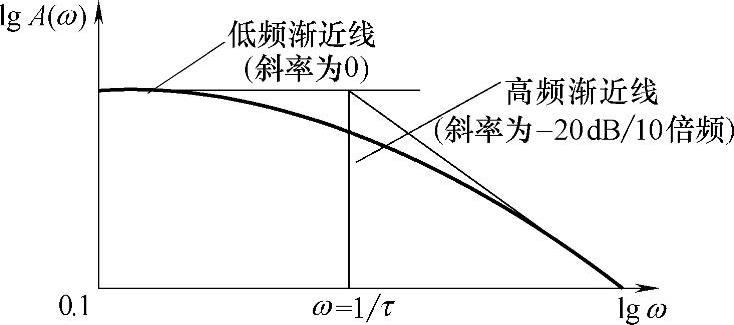
图8-23 一阶系统幅频特性

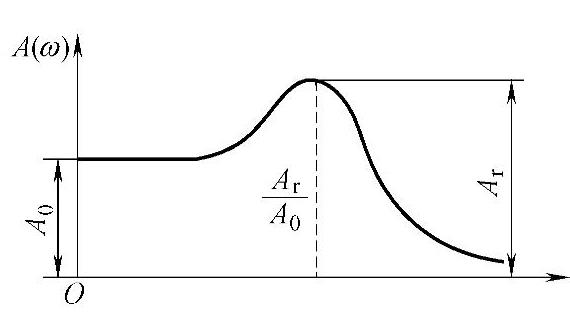
图8-24 二阶系统（ζ<1）的幅频特性

对于一阶系统，由低频渐近线（斜率为0）与高频渐近线（斜率为-20dB/10倍频）交点处，向下垂直作直线，此垂线与幅频特性相交处A（ω）=0.707，与横坐标相交点ω=1/τ，由此可以得到τ=1/ω值。

对于二阶系统，利用对二阶系统幅频特性式（8-68）求极值的方法，令式（8-68）的一阶导数为0，得

将式（8-86）代入式（8-68），得

当ω=0时，A（ω）=A₀=1。因此有

由式（8-86）、式（8-88）和图8-24可以求得ω_n和ζ。