静态特性的质量指标优化

1.迟滞

由于测试系统的机械部分的摩擦和间隙、敏感结构材料等的缺陷、磁性材料的磁滞等，致使测试系统同一个输入量的正、反行程的输出不一致，这一现象就是“迟滞”，亦称“滞环”或“回差”，如图8-5所示。

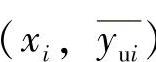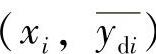对于第i个测点，其正、反行程输出的平均校准点分别为和，有

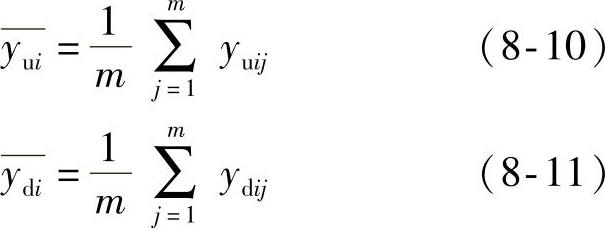
第i个测点其正、反行程的偏差为（如图8-5所示）

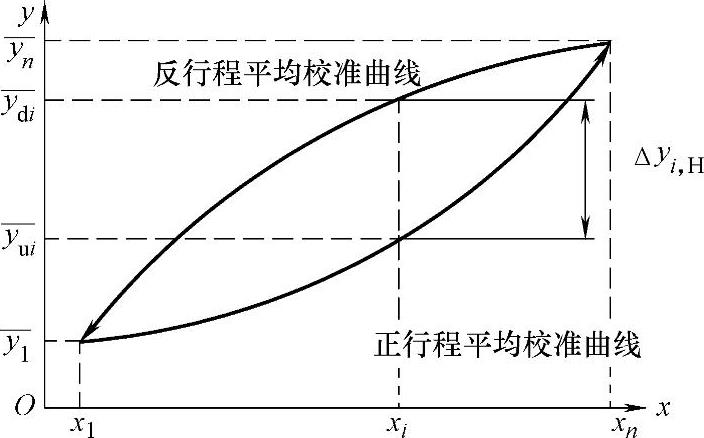
图8-5 迟滞

则迟滞产生的最大绝对误差为 （Δy_H）_max=max（Δy_i，H）（i=1，2，…，n）（8-13）

迟滞的引用误差为

式中，y_FS=y_n-y₁，为满量程的输出值。

2.重复性

同一个测点，在相同的测量条件下，测试系统按同一方向作全量程的多次重复测量时，对同一个输入量其输出值的不一致程度，如图8-6所示，其大小是随机的。为反映这一现象，引入重复性指标。

重复性反映了测试系统的随机误差，其定量评定可在重复性条件下进行多次测量，对其测量值做统计处理。

考虑正行程的第i个测点，做了m次重复测量，其平均校准值为

基于统计学的观点，将y_uij看成第i个测点正行程的子样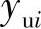，则是第i个测点正行程输出值的数学期望的估计值，可以利用贝塞尔公式来计算第i个测点的标准偏差sui。

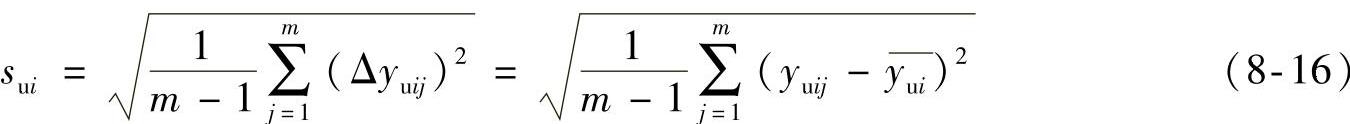
s_ui的物理意义是：当随机变量y_uij可以看成是正态分布时，y_uij偏离期望值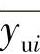的范围在（-s_ui，s_ui）之间的概率为68.37%；在（-2s_ui，2s_ui）之间的概率为95.40%；在（-3s_ui，3s_ui）之间的概率为99.73%，如图8-7所示。

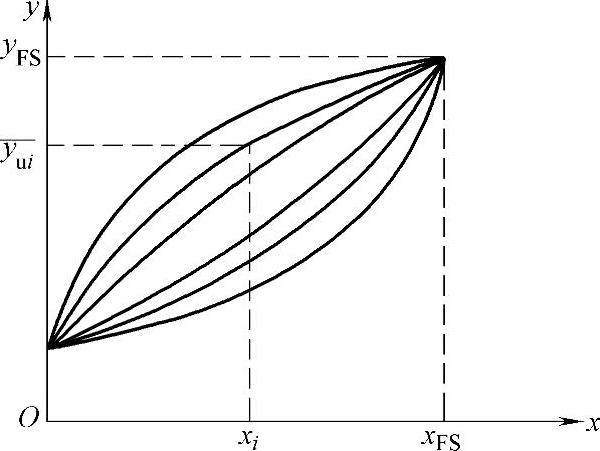
图8-6 重复性

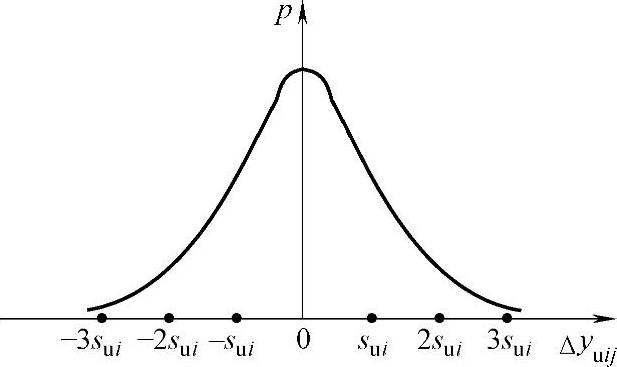
图8-7 正态分布概率曲线

类似地，可以给出第i个测点反行程的子样标准偏差S_di。

对于整个测量范围，综合考虑正反行程问题，并假设正、反行程的测量过程是等精度（等精密性）的，即正行程的子样标准偏差和反行程的子样标准偏差具有相等的数学期望。这样第i个测点的子样标准偏差为s_i，可由下式计算

对于全部n个测点，当认为是等精度测量时，可以用下式来计算整个测试过程的标准偏差

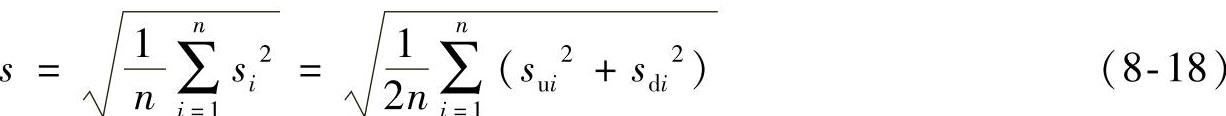
整个测试过程的标准偏差s就可以描述测试系统的随机误差，则测试系统的重复性的引用误差为

式中，y_FS为满量程的输出值，3为置信概率系数，3s为置信限或随机不确定度。其物理意义是：在整个测量范围内，测试系统相对于满量程输出的随机误差不超过δ_R的置信概率为99.73%。关于置信概率的概念已在第2章中做了详细讨论。

3.线性度

理想测量系统的输出-输入关系应当具有如式（8-3）所示的直线特性，在整个测量范围内具有相同的灵敏度，仪表刻度是均匀的。但实际上许多测量仪表，由于种种原因，其输出-输入特性总是具有不同程度的非线性。

线性度（又称非线性误差）说明测量系统实际的静态特性的校准特性与某一拟合（参考）直线不吻合程度的最大值，如图8-8所示，用引用误差形式表示为

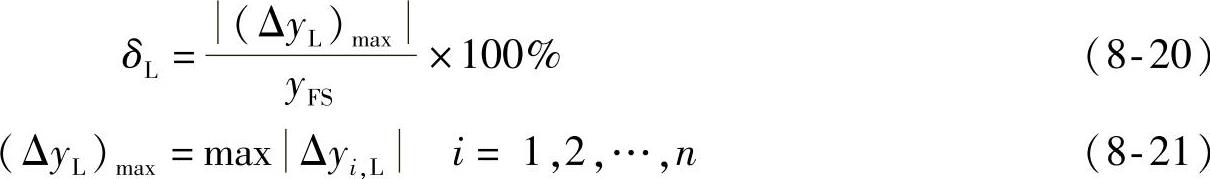
式中，y_FS为满量程输出，y_FS=|B（x_max-x_min）|，B为所选定的拟合直线的斜率。Δy_i，L是第i个校准点平均输出值与所选定的拟合直线的偏差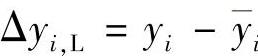，，称为非线性偏差；（Δy_L）max是n个测点中的最大偏差。

依照上述定义，选取不同的拟合曲线，计算出的线性度也不同。下面介绍几种常用的线性度的计算方法。

（1）绝对线性度δ_La

绝对线性度又称理论线性度，其拟合直线是事先规定好的，与实际标定过程和标定结果无关。通常这条拟合直线通过坐标原点（x=0，y=0）和所期望的满量程输出点（x_FS，y_FS），如图8-9所示。

（2）端基线性度δLM拟合直线是标定过程获得的两个端点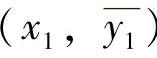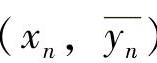，的连线，如图8-10所示。端基拟合直线为

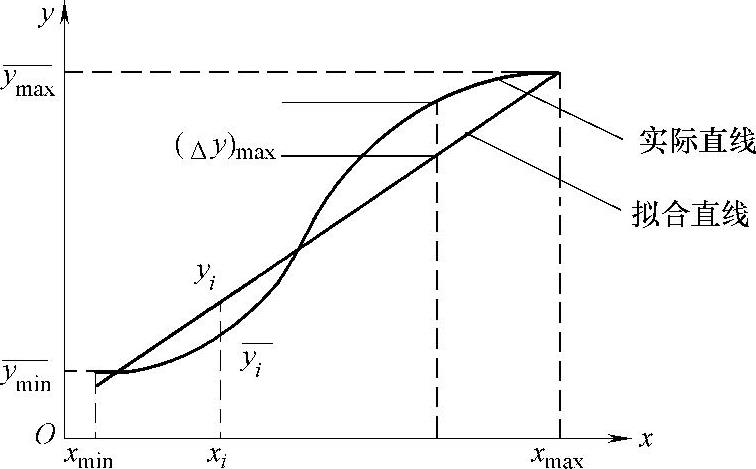
图8-8 线性度

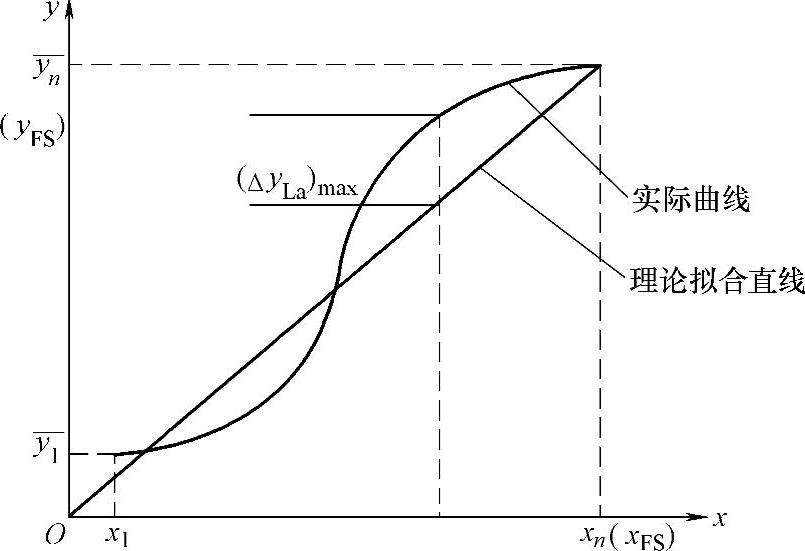
图8-9 理论拟合直线

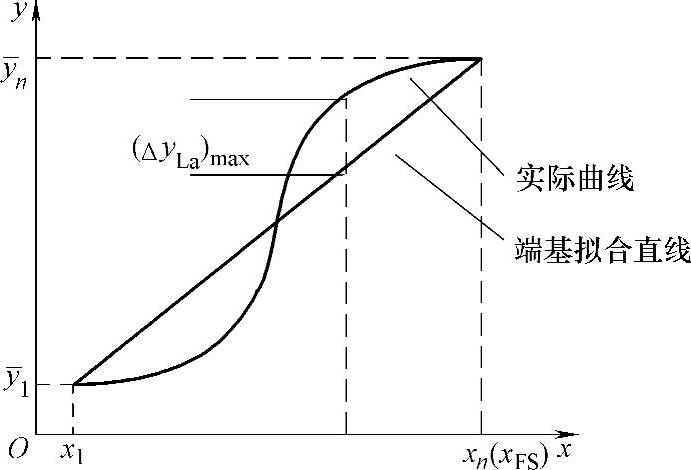
图8-10 端基拟合直线(www.xing528.com)

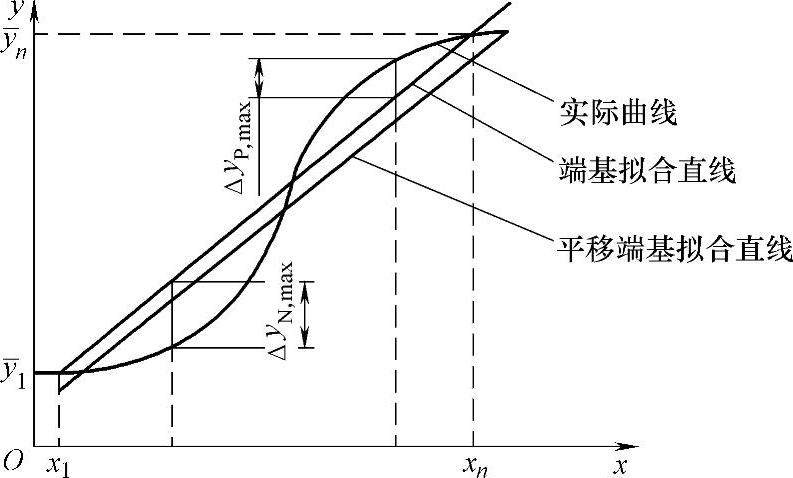
图8-11 平移端基参考直线

端基拟合直线只考虑了实际标定的两个端点，而对于其他测点的分布情况并没有考虑，因此实测点对上述拟合直线的偏差分布也不合理，最大正偏差与最大负偏差的绝对值也不会相等。为了尽可能减小最大偏差，可将端基拟合直线平移，以使最大正、负偏差绝对值相等。这样就可以得到“平移端基拟合直线”，如图8-11所示。按此直线计算得到的线性度就是“平移端基线性度”。

由式（8-23）可以计算出第i个校准点平均输出值与端基拟合直线的偏差为

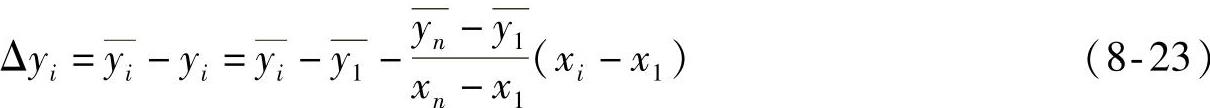
假设上述n个偏差Δy_i的最大正偏差为Δy_P，max≥0，最大负偏差Δy_N，max≤0，“平移端基拟合直线”为

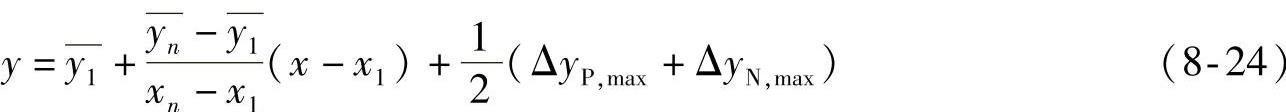
n个测点的标定值对于“平移端基拟合直线”的最大正偏差与最大负偏差的绝对值是相等的，均为

则平移端基线性度为

（3）最小二乘法线性度δLS

基于所得到的n个标定点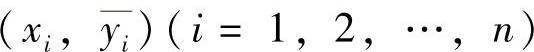，利用偏差平方和最小来确定“最小二乘法拟合直线”。

当拟合直线为 y=a+bx （8-27）

第i个测点的偏差为

总的偏差平方和为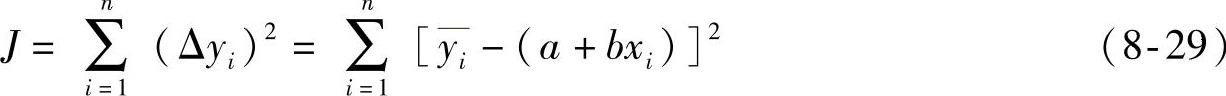

利用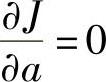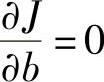，；可以得到最小二乘法拟合直线的最佳a、b值为

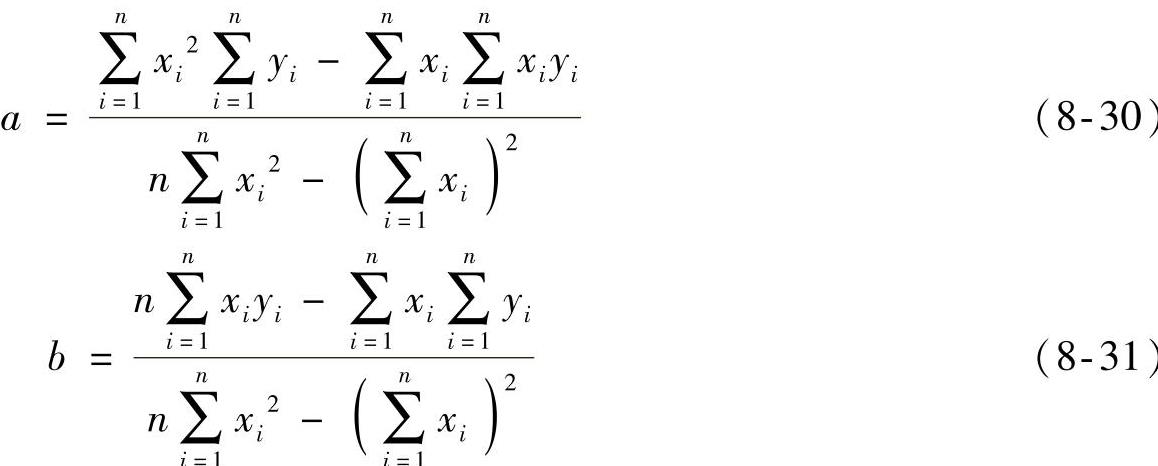
计算出a、b后，由式（8-28）可以计算出每一个测点的偏差，得到最大的偏差Δy_M，进而求出最小二乘法线性度δ_LS。关于最小二乘法的原理，已在第2章进行了讨论。

4.准确度

准确度表征测量系统给出接近于真值的响应的能力，俗称精度。虽然准确度是一种定性的概念，但实际应用中仍对它做了定量描述，有下述几种方式：

1）用准确度等级指数来表征。准确度等级指数a（表示成百分数a%FS的相对值）是以最大允许误差的大小来表征，它不是测量系统实际出现的误差。a值越小表示准确度越高。凡国家标准规定有准确度等级指数的正式产品都应有准确度等级指数的标志。

2）简化表示。一些国家标准未规定准确度等级指数的产品说明书中，常用“精度”作为一项技术指标来表征该产品的准确程度。通常精度A由线性度δ_L、迟滞δ_H和重复性δ_R之和得出，即

A=|δ_L|+|δ_H|+|δ_R|或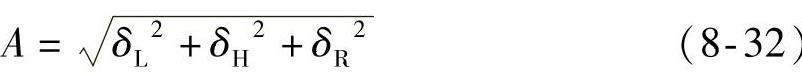

用式（8-32）来表征准确度是不完善的，它只是一种粗略的简化表示。

3）用不确定度（或误差）来表征。测量系统或测量装置的不确定度为在规定条件下系统或装置用于测量时所得测量结果的不确定度。关于不确定度已在第2章进行了讨论。

5.稳定性

稳定性是表征测量系统保持其计量特性恒定不变的能力。稳定性通常是对时间而言的，即计量特性变化到给定量需要的最少时间，或计量特性在给定时间内所发生的变化的范围。当稳定性不是对时间而是对其他量而言时，应根据有关技术文件规定的方法进行评定。

与稳定性密切相关的一个概念是漂移。测量系统的漂移是在一定时间内或某一影响量作用范围内（根据技术规范要求）计量特性的慢变化。

（1）时漂

当测试系统的输入和环境温度不变时，输出量随时间变化的现象就是漂移，又称时漂。它是由于测试系统内部各个环节性能不稳定或内部温度变化引起的，反映了测试系统的稳定性指标。通常考察测试系统时漂的时间范围可以是一个小时、一天、一个月、半年或一年。

测量系统的漂移和稳定性通常是针对时间而言的，前者着重说明在一次开机使用期间计量特性变化的大小和规律；后者着重说明长期、多次使用，在相同工作状态下保持计量特性的能力。通过漂移可确定仪器的工作条件和预热周期，以保证仪器工作在一个稳定的状态；稳定性可以估计仪器计量特性保持有效的周期。

（2）温漂

由外界环境温度变化引起的输出量变化的现象称为温漂。温漂可以从两个方面来考察。一方面是零点漂移，即测试系统零点处的温漂，反映了温度变化引起的测试系统特性平移而斜率不变的漂移；另一方面是灵敏度温漂，即引起测试系统特性斜率变化的漂移。

零点漂移ν和灵敏度漂移β可由下面两式来计算

式中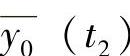，为在规定的温度（高温或低温）t₂保温一小时后，测试系统零点输出的平均值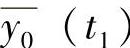；为在室温t₁时，测试系统零点输出的平均值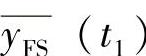；为在室温t₁时，测试系统满量程输出的平均值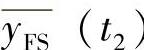；为在规定的温度（高温或低温）t₂保温一小时后，测试系统满量程输出的平均值。

（3）影响系数

影响仪器计量特性的量通常有温度、大气压、振动、电源电压和频率等。当仪器的实际工作条件偏离基准工作条件时，将使仪器计量特性发生变化，对仪器的示值产生影响。其影响常用影响系数来表示，即用指示值变化与影响量变化的比值（常用引用误差）来表示。例如，某仪器的温度影响系数为3.4×10^-4/℃，表示温度变化1℃引起指示值的变化为3.4×10^-4（引用误差）。

6.可靠性

一台装置的可靠性是指该装置可在规定的时期内及在保持其运行指标不超限的情况下执行其功能的性能。它是反映产品是否耐用的一项综合指标。可靠性指标有：

1）平均无故障时间MTBF（Mean Time Between Failure）：在标准工作条件下不间断地工作，直到发生故障而失去工作能力的时间称为无故障时间。如果取若干次（或若干台仪器）无故障时间求其平均值，则为平均无故障时间，它表示相邻两次故障间隔时间的平均值。

2）故障率或失效率：它是平均无故障时间MTBF的倒数。某仪器的失效率为0.03%/kh，就是说若有1万台仪器工作1000h后，在这段时间里只可能有3台会出现故障。

3）可信任概率P：表征由于元件参数的渐变而使仪表误差在给定时间内仍然保持在技术条件规定限度以内的概率。显然，概率P值越大，测量仪器的可靠性越高，测量仪器的成本也越高。

可靠性在产品设计与生产中具有深远的指导意义，越来越引起人们的关注与重视。

7.输入阻抗与输出阻抗

输入阻抗与输出阻抗值对于组成测量系统的各环节而言甚为重要。希望前级输出信号无损失地向后级传送，信号源的内阻应为零，后级输入阻抗理想值为无限大。这样，前后环节则为相互独立的环节。为了消除各环节的影响，在各环节之间设置阻抗变换器。