化学中的析晶活化能探讨

玻璃为亚稳相，将玻璃加热到某一温度会发生结晶而放热，因而在差热分析曲线上会出现放热峰，放热峰的开始温度为初始析晶温度Tx，放热峰温度为析晶峰温度TC，并且Tx随加热速率φ的变化而变化。通过这些参数可以研究多组分玻璃体系的稳定程度，前人利用各种不同的计算方法，对玻璃的热稳定性进行判断。

D.Uhlmann［144］最早提出用玻璃特征温度来判别玻璃稳定性，初始析晶温度Tx和玻璃转变温度Tm的差值ΔT与玻璃的稳定性有一定关系，ΔT越大，玻璃的稳定性越好。T.Iqbal等［145］指出，决定玻璃形成能力的是玻璃在熔点时的黏度及其随温度的变化，而对一组具有相同黏度－温度关系的物质，具有较低熔点的物质易形成玻璃。据此提出用初始析晶温度和玻璃转变温度之比（TC／Tm）来判别玻璃的稳定性，同时认为用临界冷却速率R可以判断形成玻璃能力，但由于R较难精确测定，此判据不能用于判断析晶倾向接近的玻璃的热稳定性。

T.Iqbal等［146］首次将热力学参数与动力学参数结合起来，提出用ST＝（Tx－TC）／R来判断玻璃的稳定性。ST判据综合了玻璃形成的热力学与动力学因素，能比较准确地反映玻璃的稳定性，但同样由于临界速率R很难精确测定，因而限制了其适用范围。S.Surlnach等［147］在采用DTA研究玻璃析晶行为时，引入动力学析晶参数k（TC）来衡量玻璃析晶的难易，认为k（TC）越小，玻璃越稳定。胡丽丽等［148］则提出采用动力学析晶参数k（T）或析晶峰温度TC时的k（TC）来判断玻璃的稳定性。k（T）或k（TC）值越小，玻璃越稳定。k（T）或k（TC）判据可以较好地判断同一玻璃体系的稳定性，但由于其受升温速率φ和温度的影响较大，因而限制了其适用范围。

研究发现，析晶活化能可以在一定程度上反映玻璃析晶的难易程度，由于非晶态向晶态转变时，需要一定的析晶势垒，因此，析晶活化能是研究析晶动力学的有效手段之一。本文利用JMA方程计算析晶活化能E和晶体生长指数n。

采用DTA研究析晶动力学时，H.E.Kissinger等［149］运用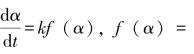（1－α）n和Arrhenius方程得：

式中：α为相转变分数（%）；

　　　n为析晶参数；

　　　t为加热时间（min）；

　　　k为比例常数；

　　　A为频率因子；

　　　E为析晶活化能（kJ／mol）；

　　　R为气体常数；

　　　T为温度（K）。

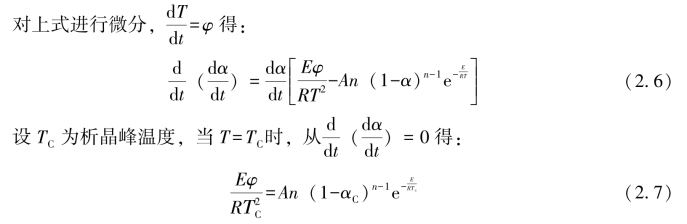
DTA曲线上不能直接确定上式中未知反应物的相变分数（1－αC），不妨先对式（2.5）积分：

(www.xing528.com)

将式（2.7）与式（2.9）合并后得：

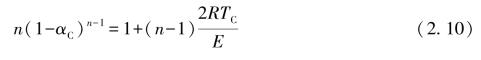
由于式（2.10）与φ无关，且一般E≥RTC，故（n－1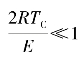），即n（1－αC）n－1≈1。将其代入式（2.10）得：

对方程两边取对数得：

式中：αC为相转变分数；

　　　TC为析晶峰温度（K）；

　　　φ为升温速率（℃／min）。

因此，可以利用公式（2.12）进行计算，由对作图，可得一条直线，如图2.9所示，斜率为。由此计算可以确定在不同CaO和Al2O3质量分数条件下的析晶活化能，如图2.10和图2.11所示。从图2.10中可以看出，随着CaO质量分数的增加，CaO－Al2O3－SiO2－Na2O系玻璃的析晶活化能呈降低的趋势，说明随着CaO质量分数的增加，熔体的稳定性降低，玻璃的析晶倾向增大。

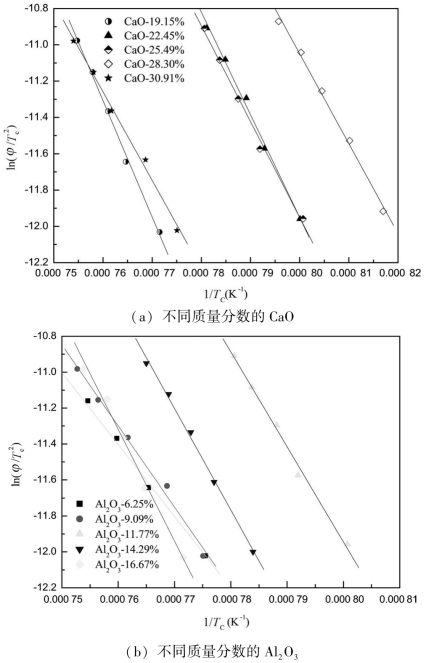
图2.9　试样的Kissinger曲线

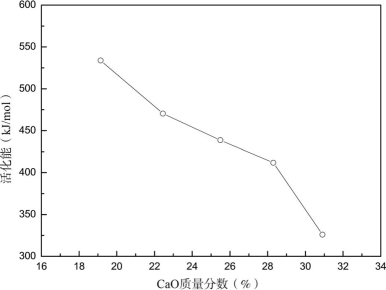
图2.10　CaO质量分数与析晶活化能的关系

Al2O3质量分数对析晶活化能的影响作用如图2.11所示。从图2.11中可以看出，随着Al2O3质量分数的增加，CaO－Al2O3－SiO2－Na2O系玻璃的析晶活化能逐渐升高。说明随着Al2O3质量分数的增加，熔体的网络聚合程度也随之增大，玻璃的稳定性增强，这不利于玻璃相中晶体的析出。

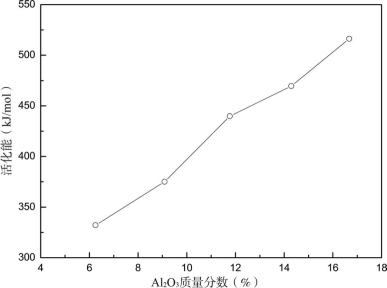
图2.11　Al2O3质量分数与析晶活化能的关系