机械振动的分析与控制：迭代求解特征值问题介绍

特征值和特征向量作为一对特征参数，可以由迭代法来求解。可以对特征向量进行迭代，得到特征向量后，再算出对应的特征值；也可以对特征值进行迭代，得到特征值后，再计算对应的特征向量。

1.特征向量迭代法

我们考虑机械动力学系统的特征值问题

Kφ=λMφ （5.63）

M，K分别表示质量矩阵和刚性矩阵。方程式（5.63）形式上类似于静态问题的方程Kx=F，因此可以利用5.1.2节中的迭代解法的思路来求解这个特征值问题。

假定特征值的初始值为λ=1，初估的特征向量为x₁，则方程式（5.63）右边为R₁=Mx₁。由于这是一个初估值，一般并不满足Kx₁=R₁，否则，x₁就是所要的特征向量。但是，我们可以根据方程式（5.63）构建以下迭代关系

Kx₂=R₁

其中，x₂为一个新的特征向量估计。依次进行若干次迭代，就可以得到逼近真值的特征向量，这就是向量迭代法的基本原理。

以上迭代过程最先求到的是与最小特征值所对应的特征向量，其迭代原理可以用下式表示

由于原理上涉及刚性矩阵的逆，这个方法称为逆迭代法（Inverse Iteration），是求解特征值问题重要的迭代方法。当然，在实际运算中，并不进行矩阵的求逆运算，而是对刚性矩阵进行三角分解，即迭代过程是基于式（5.65）进行的

当i→∞时，x_i+1→φ₁。

另外，为了用模态质量对特征向量进行正规化，即为了使最终的特征向量满足

需要对上述迭代过程做以下修改

以上所述仅仅是迭代法的原理，实际的算法按以下更加有效的步骤进行

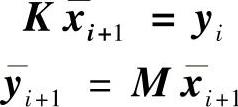
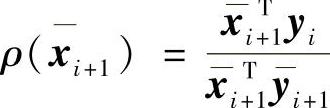→瑞利商（Rayleigh Quotient）

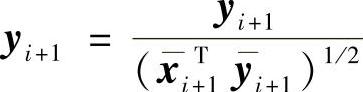
当i趋近于∞时，y_i+1趋近于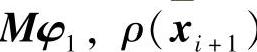趋近于λ₁。

逆迭代法最先收敛于最低的特征值。各个特征值分开得越远，收敛速度越快。为了改进收敛速度，或者求解指定频率附近的特征值与特征向量，经常结合使用移位法（Shifting）。具体请参阅有关书籍。

如果把式（5.63）的左边作为输入，右边作为输出，则可以构建以下形式的迭代关系

Mx_i+1=Kx_i(www.xing528.com)

由此可以求得与最大特征值对应的特征向量。这种正向迭代方法通常称为幂法（因为在迭代过程中，相当于矩阵K的各次幂作用于向量x）。由于在结构分析中，通常所需的是结构的低阶固有值和模态，所以相对于幂法，逆迭代法（又称逆幂法）更为常用。

2.特征值迭代法

特征值迭代法是针对n阶特征方程来进行的（行列式用det表示）

det（K-λM）=0 （5.68）

最直接的方法就是将上述行列式展开，得到关于λ的n次多项式函数，用牛顿迭代法求解多项式的零点，即得特征值的解。但是，这种方法只适用于n较小的情况。对于大规模系统来说，计算多项式的系数是非常困难的工作。因此在实际中，这种方法是不被采用的。

这里，我们介绍利用矩阵分解来计算行列式值的方法。令

p（λ）=det（K-λM） （5.69）

对于大多数线性动力学系统来说，K-λM为对称矩阵，利用Cholesky分解，得

K_-λM=LDL^T （5.70）

这时，K-λM的行列式满足下列关系

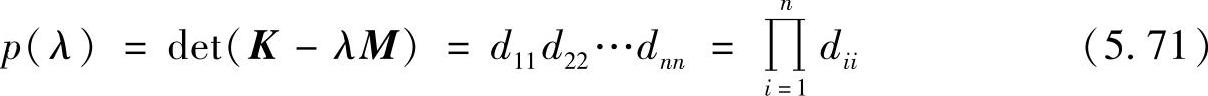
这里，d_ii为对角阵D的元素。这样，给定一个λ值，进行矩阵分解，再根据式（5.71），就可以计算出与之对应的行列式的值p（λ）。

在此基础上，我们利用拟牛顿迭代法来求解方程p（λ）=0的根。

参照图5.13，假定λ₁^（k）是对最小特征值λ₁的第k次迭代的近似值，则根据拟牛顿迭代法，可以得到以下迭代关系（弦切法）

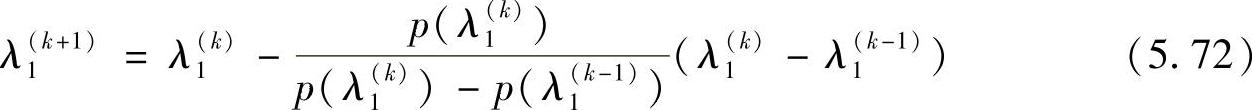
利用该关系进行若干次迭代，即可得到λ₁。这里，对于每次更新的λ₁^（k）所对应的行列式的值p（λ₁^（k）），利用式（5.71）进行计算。这样就回避了直接求解多项式系数的问题。

最后，我们介绍Sturm序列在求解特征值中的应用。

在结构动力学分析中，往往需要求出给定范围的固有频率，即求解λ_l＜λ＜λ_u范围的特征值。因此，首先需要判断在此范围有多少个特征值，然后把每个特征值分离开来，在各个局部范围上应用上述迭代方法，可以求出每个特征值来。

Sturm序列（Sturm Sequence）是确定一个多项式的根的个数的数学方法。例如要想知道在λ_l以下存在多少个特征值，可以对矩阵K-λ_lM进行Cholesky分解

K-λ_lM=LDL^T

对角矩阵D中，负的元素的个数就是小于λ_l的特征值的个数。这就是Sturm序列的性质。利用这个方法，可以得到λ_l＜λ＜λ_u范围上的特征值的个数，再反复利用2分法，就可以把每个特征值分离出来。然后，在每个特征值附近应用拟牛顿迭代法，可求出每个特征值的准确值。得到特征值之后，如有需要，可以根据1.中所介绍的迭代方法求得特征向量。

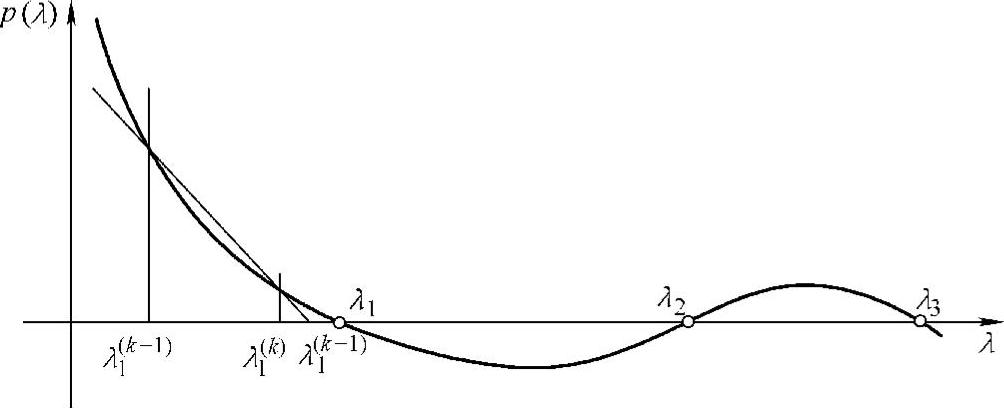
图5.13 求解λ₁的拟牛顿迭代法