求解动力学方程的数值积分方法

机械系统的动力学特征是由2阶微分方程所决定的。例如单自由度系统的线性振动特性由下式确定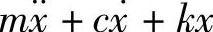，=f。对于这类简单情况，尚且可以求出其解析解；而对于实际的复杂系统，则要用有限元方法进行数值计算。由于求解动力学问题是数值积分方法在机械工程领域应用的重要方面，因此，这里单独作为一节进行介绍。

1.中心差分方法（Central Difference Method）

相对于向前差分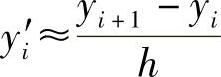以及向后差分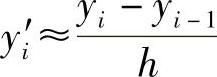，中心差分的定义为

为了研究中心差分的精度，应用泰勒展开式

式（5.46a）和（5.46b）相减后，变形得y_i′的值为

其中，y_i^（3）（ξ）=[y_i^（3）（ξ₁）+y_i^（3）（ξ₂）]/2（中值定理）。把式（5.47）与（5.45）相比，可见中心差分的精度为2阶。相比之下，向前差分及向后差分只有1阶精度。由于中心差分方法形式简单而且具有2阶精度，在结构以及流体动力学计算中得到广泛应用。

由式（5.45）即可得到下列递推公式

可见，中心差分法是显式解法，上式也是多步法的最简单形式。下面，对该方法在结构动力学中的运用做一介绍。

考虑到非线性等一般情况，在t时刻，系统的运动方程可写成以下形式

其中，M为质量矩阵，Q代表系统内力，P为外力，u为位移响应（对于线性系统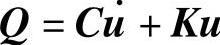，，C、K分别为阻尼矩阵和刚性矩阵）。为了简单，这里只考虑积分步长Δt一定的情况。我们的目标是求解下一个时刻（t+Δt）的位移。

由式（5.48）可得

引入半步长Δt/2，在区间（t-Δt/2，t+Δt/2）上应用中心差分法，可求得（t+Δt/

2）时刻的速度为

进一步在区间（t，t+Δt）上应用中心差分法，可求得（t+Δt）时刻的位移为

以上式（5.49）、（5.50）、（5.51）3个公式逐次运算，即可求得各个时刻的加速度、速度及位移。具体地说，由位移、速度的初始条件，可得到初始状态的内力，应用公式（5.49）可求得初始加速度，然后由式（5.50）和（5.51）依次计算下一个时刻的速度和位移。得到速度和位移后，再应用式（5.49）求得该时刻的加速度，这样逐次递推下去。应注意：在计算（t+Δt）时刻的内力Q_t+Δt时，u_t+Δt已知，但是该时刻的速度为未知，因此，需要用（t+Δt/2）时刻的值来近似（t+Δt）时刻的值，即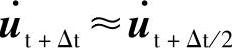。同样，对于t时刻，需要做近似。

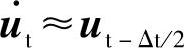中心差分法是依次向前递推，没有迭代运算，不需要更新切线刚性；同时，由于内力向量由单个元素来构建，也不需要整体刚性矩阵。这些特点使得每步的运算很简单。但是，式（5.49）中含有质量矩阵的逆运算，比较费时。为了最大发挥显式解法的特长，在有限元建模时，通常采用集中质量模型（Lumped Mass）。这样的话，M为对角矩阵，求逆运算变得很容易。

可以证明，当积分步长趋于0时，中心差分法的计算结果将趋于真值；反之，当积分步长大于某临界值时，计算将发散。这种现象称为中心差分法的条件稳定性。也就是说，在应用中心差分法时，必须使用小于临界值的积分步长。在已知系统的最大固有频率ω_max及其阻尼比ζ的情况下，临界积分步长由式（5.52）确定

但是，复杂系统的最高固有频率及其阻尼比往往事先无法知道，在有限元方法中，常用下列公式估算临界积分步长

Δt_c=L^e/c_d这里，L^e为元素的特征边长，c_d为机械波的传播速度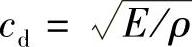，，E代表材料的弹性模量（Young’s Modulus），ρ代表密度。简单地说，有限元模型划分得越细，所用的积分步长越要小。例如对于钢材料，E=2.1e+11（N/m²），ρ=7800kg/m³，如果假定所划分单元的代表长度L^e=10mm，则可估算出临界积分步长为1.93e-6秒。对于大规模有限元模型，用这样小的步长来计算瞬态响应是很费时的事。因此，中心差分法主要用于计算时间历程很短、具有很强非线性的现象，例如安全气囊展开、汽车碰撞等。

最后需要注意的是，由于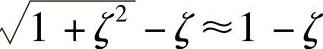，由式（5.52）可知，增加阻尼反而会减小临界积分步长，从而增加计算时间。

2.Newmark积分法

在1959年，Newmark提出了求解结构动力学问题的数值积分方法。时至今日，该方法已得到广泛应用，并且衍变出了许多不同的形式。这里对该方法重点加以介绍。

我们已经知道，在应用中心差分法时，首先由运动方程解得加速度，然后用中心差分原理近似求解速度及位移。在此，直接应用泰勒级数来表示速度及位移的真值

上两式右边最后一项表示泰勒级数的余项。ξ为区间（t，t+Δt）上的某值。New_-mark把上两式保留到项，并引入位于区间[0，1]上的两个常数β、γ，给出下列公式

进一步假定在区间（t，t+Δt）上加速度呈线性分布，于是得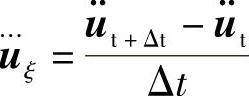。代入以上公式，可得Newmark积分的标准形式为

β≠0时，式（5.53a）和（5.53b）右边包含有（t+Δt）时刻的加速度，因此属于隐式解法的形式。加速度由动力平衡方程式决定。例如对于线性系统，有

将式（5.53a）和（5.53b）代入并整理，得

在已知初始位移u₀及初速度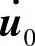的情况下，初始加速度可由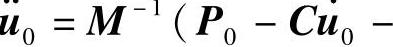Ku₀）得到。于是，求解方程式（5.55），即可得下一个时刻的加速度，然后再由式（5.53）计算速度和位移。

在以上运算中，首先需要求解方程（5.55），以得到未知量加速度。但是，在实际应用中，常希望把位移作为未知量。为此，需要对式（5.53）进行变形。由式（5.53b）可得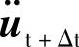，再代入到式（5.53a）整理，得

把式（5.56）代入方程式（5.54），便可得到未知量为位移的关系式

由上式得到位移u_t+Δt后，再由式（5.56）计算速度和加速度。

对于非线性系统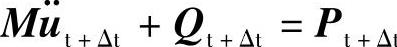，，需要用Newton-Raphson法进行迭代运算。为了叙述方便，略去阻尼项，将内力向量线性化处理，有

这里，上标i表示迭代运算的回数。并且(www.xing528.com)

表示第i回迭代运算内位移的变化量，i=1时，。同样，可以定义加速度的变化量

于是，由动力平衡方程式可以得到以下迭代公式

式（5.57）中存在2个未知数，Δu^（i）_t+Δt和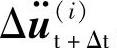。应用公式（5.53b）来考察二者的关系。对于第i回迭代运算和第i-1回迭代运算，由公式（5.53b）可得下列关系式

两式相减，得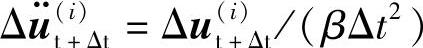。将此关系代入式（5.57），即可得到只有一个未知数Δu^（i）_t+Δt的方程

由上式可求得第i回迭代运算的位移变化量，进而可以得到速度和加速度。当迭代运算的收敛精度达到要求时，迭代运算结束，最终得到（t+Δt）时刻的各个物理量。把位移作为未知数来进行迭代运算比把加速度作为未知数来进行迭代运算要好得多，因为加速度往往不连续，这是把式（5.53）变形为式（5.56）进行运算的原因。

3.Newmark积分法的变形

在Newmark积分公式中，常数β、γ的取值确定了积分的稳定性以及精度。通过这两个常数的特定组合，可以衍变出多种古典的积分方法来。

当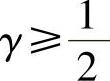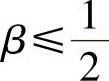，时，Newmark积分法具有条件稳定性，积分步长需满足关系

当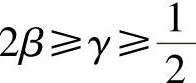时，Newmark积分法具有无条件稳定性，原则上积分步长不受限制。在实际应用中，为了较准确地预测出系统响应的波形，通常把积分步长限制在所需最短周期成分的1/10以下。

（1）γ=1/2，β=1/4

在这种情况下，Newmark积分法变为古典的平均加速度法。式（5.53）成为

平均加速度法是假定在区间（t，t+Δt）上加速度一定，等于两端点值的平均值，即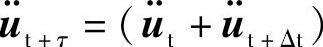/2，0≤τ≤Δt。对此式两边求积分，并利用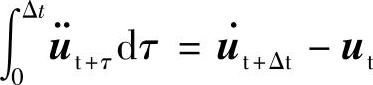，即可得到式（5.58）。形式上，式（5.58）相当于匀加速运动的速度和位移的计算公式。

平均加速度法相当于用梯形法则来近似区间上的加速度，因此和梯形积分法则一样具有2阶计算精度。这个方法属于隐式算法，具有无条件稳定性。这是New-mark积分最常用的形式（事实上，当γ=1/2时，Newmark积分的各种形式均具有2阶计算精度；当γ≠1/2时，则只有1阶精度）。

（2）γ=1/2，β=1/6

这时，式（5.53）成为

在加速度为线性变化的情况下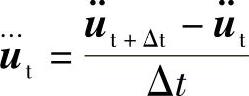，，3阶以上的微分为0，由泰勒级数可直接得到上式。这个方法称为线性加速度法。该法不具有无条件稳定性，在实际解析中应用不多。

（3）γ=1/2，β=0

此时，式（5.53a）成为

由于Newmark积分法假定在区间（t，t+Δt）上的加速度呈线性变化，因此上式中的两端点的加速度平均值等于半步长（t+Δt/2）时的加速度值。因此，上式可以进一步写成

该式等价于

另一方面，式（5.53b）成为

式（5.59）同式（5.50）相同；也容易发现式（5.60）同式（5.51）等价[利用关系式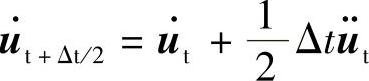，将式（5.51）变形，即得式（5.60）]。因此，这种情况下的Newmark积分法相当于中心差分法，属于显式解法，也具有2阶计算精度，但只有条件稳定性。

4.Hilber-Hughes-Taylor（HHT）积分法

在Newmark方法被提出以后，许多人对该方法进行了改进和发展，从而衍变出多种形式来。这里介绍被商业计算软件广为采用的Hilber-Hughes-Taylor方法，简称HHT法。

Newmark隐式算法（γ=1/2，β=1/4）理论上具有2阶精度及无条件稳定性，但该方法也有一个缺点，就是在其算法中不能定义数值阻尼。之所以要引入数值阻尼，是因为复杂系统中存在许多远在所需频率之外的高频成分，其振动周期可能比积分步长还要小。当边界条件及外载荷发生变化时，甚至在积分步长改变时，这些高频成分会被激励起来，形成数值“噪声”，影响计算精度及稳定性。因此，需要定义数值阻尼来衰减这些高频“噪声”。引入数值阻尼的另一个好处是可以提高非线性系统的稳定性。Newmark隐式算法的无条件稳定性是对线性系统而言的，而对于非线性系统，并无严格的保证。数值阻尼可以消除或降低不稳定因素的影响。关于数值阻尼的详细数学描述，请参阅有关书籍。

既保持无条件稳定性，又可以定义数值阻尼的计算方法中，较有名的有Wil-son-θ法、Houbolt法以及在γ>1/2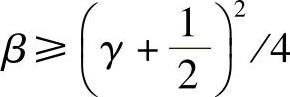，条件下的Newmark法。但是，这些方法的数值阻尼对低频模态影响较大（尤其是后两者），以致计算精度不高。所以，现在常用更优越的HHT法。

HHT法既保持了Newmark隐式算法的无条件稳定性，又保持了2阶计算精度，而且通过一个参数就可以自由调节数值阻尼的大小，同时对低频模态影响不大。

HHT法并没有改变Newmark法的积分形式（5.53），而是引入常数α，对内力和外力向量做以下修改

从而把运动方程改写为

其中，内力向量为位移及速度的函数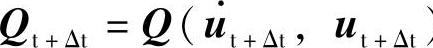，）。α的取值范围为[-1/3，0]，Newmark法的常数β、γ同α有以下关系

当α=0时，HHT法蜕变为标准的Newmark隐式算法；当α=-1/3时，将会产生很大的数值阻尼。一般取α=-0.05。