如何近似解定积分

1.矩形法则（Rectangle Rule）

求定积分的近似解，最简单的方法就是把函数f（x）在积分区间上当作一个定值，例如用左端点的值来近似所有点的值，即f（x）≈f（a），x∈[a，b]，可得

这就是最简单的矩形法则。当然，也可以用右端点数据来进行矩形近似，即f（x）≈f（b）。很显然，只有当区间长度很小时，这种方法才有意义。因此，在实际应用中，得把积分区间分成许多等份，在每个小等份，即1个积分步长上应用矩形法则。

为了对矩形法则的误差做一个简单估计，假设函数f（x）的1阶微分存在并连续，用泰勒级数把f（x）在x=a处展开，有

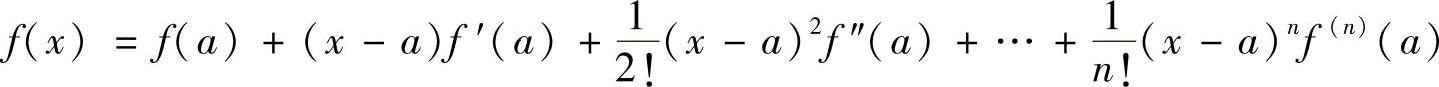
于是可得积分的真值为

其中，h=b-a。上式右边第一项代表由矩形法则所得的积分值，第二项以后代表矩形法则的误差。由于误差主要由积分步长h的2次方的项所决定，因此称为2次误差。换言之，用端点近似的矩形法则仅具有1阶计算精度（仅精确到步长的1次方的项）。

如果用中间值进行矩形近似，即，可以改进计算精度，但更常用的是采用下述梯形法则。

2.梯形法则（Trapezoidal Rule）

矩形法则把区间（积分步长）上的f（x）当作一定值，而梯形法则则是把f（x）当作线性变化的1次函数。如图5.10所示，把两个端点的值f（a）、f（b）用直线连接起来，形成一个梯形。这时，f（x）可以用以下线性函数来近似

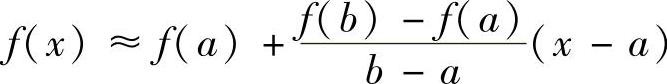
梯形的面积就是积分的近似值，即

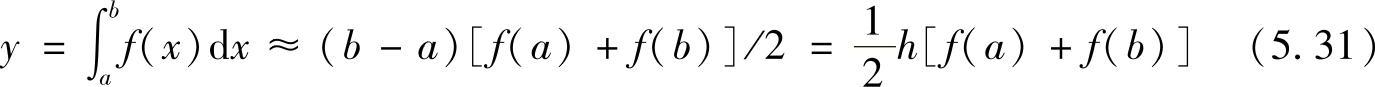
显然，把两端点的函数值的平均当作区间上的函数值，即，可以直接得到式（5.31）。

将式（5.31）中的f（b）用泰勒级数展开，得

代入式（5.31）中，可得

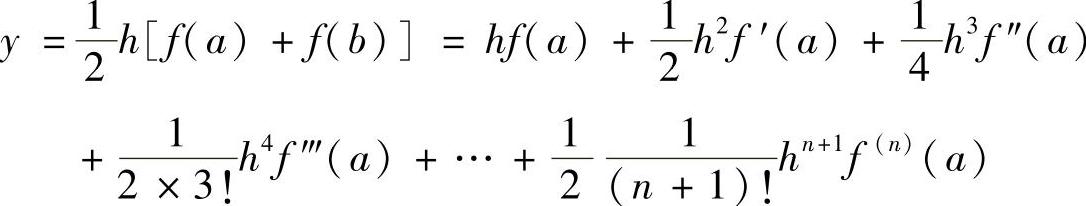
与真值相比可知，梯形法则的误差从h³的项开始，即3次误差，2阶计算精度。

图5.10 梯形法则示意图

3.Simpson法则

Simpson法则是用一个2次函数来近似f（x）。为此，需要利用两端点a、b及中间点m=（a+b）/2共3个数据点来构成以下多项式

积分的近似值为

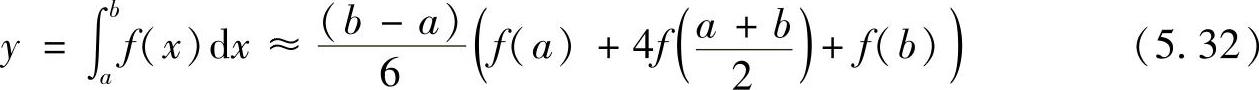
Simpson法则为5次误差，4阶计算精度。

4.Newton-Cotes法则

把区间[a，b]等分为m份，形成m+1个数据点。用多项式插值原理来构建m次函数，以逼近f（x）(www.xing528.com)

由于该函数经过每一个数据点，从而有f_m（x_i）=y_i，i∈{0，1，…，m}。于是，可以列出m+1个线性方程组，从而求得多项式的系数。也就是说，这个多项式是唯一确定的。

Newton-Cotes法则是把该多项式写为拉格朗日多项式（Lagrange Polynomial）的形式

所以，积分的近似值为

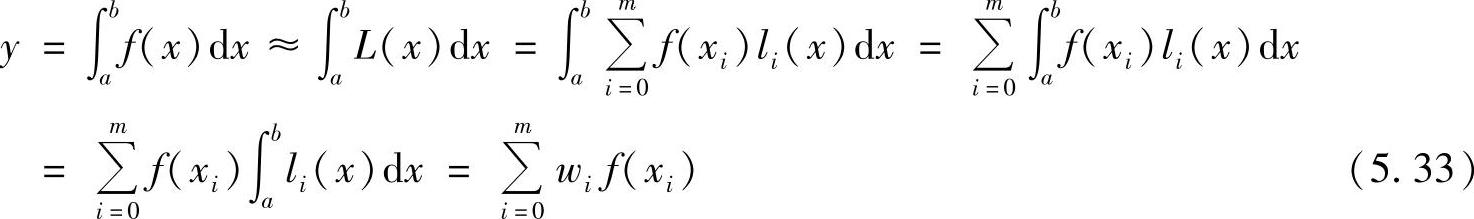
这里，是由多项式确定的加权系数。

前述矩形法则、梯形法则、Simpson法则都是Newton-Cotes法则的特殊形式。Newton-Cotes法则又分为两种形式：利用区间[a，b]两端点的值进行计算的方法称为Closed Newton-Cotes法；相反，不用两端点的值进行计算的方法称为Open New-ton-Cotes法。用公式可以表达为

在用Newton-Cotes法则时，如果m取值过大，反而会引起数值振荡。因此，往往m取值不大，而是把区间[a，b]细分，在每个小区间上应用该近似法则，然后把所有区间上的值加起来，即得区间[a，b]上的积分值。例如把区间[a，b]分为n等份，应用梯形法则（m=1），可得

5.高斯积分（Gaussian Quadrature）

以上介绍的积分方法均是在积分区间上用等间隔分布的离散数据点来构建多项式插值函数，而高斯积分方法则是寻找不等间隔的最优数据点分布，从而达到在较少或相同数目的数据点的情况下提高积分精度的目的。高斯积分的形式为

这里，x_i是选择的离散数据点，w_i是相应的加权系数。并且已知，当x_i处于一个正交多项式的零点时，式（5.34）的积分的误差最小。因此，高斯积分方法的重要任务就是寻找这样的一个正交多项式，以构建一个插值函数。

所谓正交多项式，是指具有下列性质的多项式。设一个n次正交多项式为T_n（x），则有性质：

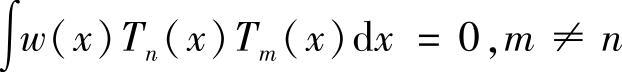
切比雪夫多项式（Chebyshev Polynomials）就是高斯积分方法常用的正交多项式。详细内容在这里就不做介绍，下面仅从一个简单的例子来看看高斯积分的优点。

考虑积分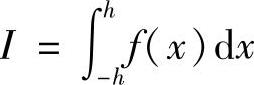。把f（x）用泰勒级数在原点展开，有

则该积分的严密解为

现在，我们用两个数据点x₁、x₂来估计该积分，即

我们的目的是选择x₁、x₂以及w₁、w₂，以使得I和I_E的差最小。通过对比I和I_E的系数，可得

这四个方程就确定了x₁、x₂以及w₁、w₂：，，w₁=h，w₂=h。

也就是说，从f^（4）（0）的项开始，I和I_E开始不一致。因此，误差包含f^（4）（0）的项，其系数为。即误差为5次，精度为4阶。积分的精确值可以写成

可见，通过优选数据点，高斯积分用两个数据点就可以达到4阶计算精度；而同样用两个数据点的梯形法，则只有2阶计算精度。