牛顿迭代法在非线性有限元分析中的优势

前面以一个单自由度系统（一元方程）为例，介绍了牛顿迭代法求解非线性方程的原理。这里，我们以更一般的复杂系统为对象，介绍牛顿迭代法在结构非线性有限元分析中的应用。

图5.8所示为结构有限元分析中的外力与内力的示意图。结构时刻处于静力平衡状态的条件是外力P与内力Q相互平衡，即

P-Q=0 （5.24）上式是求解结构在外力作用下的非线性变形（响应）的出发点。由于不能直接求解方程式（5.24），一般把外力的作用由0逐渐到P分为若干步作用到结构上去。在这个过程中，利用迭代方法求解结构的变形或者响应。对于静态问题来说，这个载荷随时间变化的历程是一个不具有实际含义的假想过程；而对于动态问题来说，载荷随时间的变化则具有实际的物理含义。下面以静态问题的求解为例，来说明牛顿迭代法的运用。

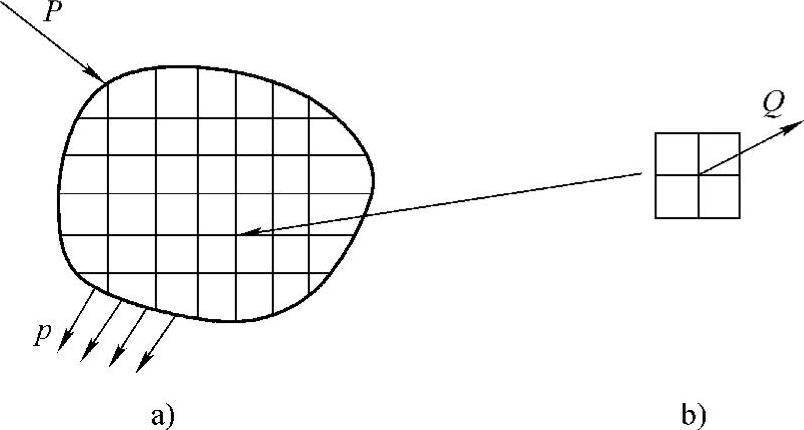
图5.8 作用在结构上的外力和结构内部的内力

a）外界载荷 b）节点内力

假定外力不随结构变形而变化，并且在时刻t已经得到了结构的变形向量X^t，现在的任务是求下一个时刻（t+Δt）的变形X^t+Δt。因此，构建一个函数

方程f（X）=0的根即是所要的结果。设该方程的根为X^∗，用迭代法求解该方程，并假定迭代进行到第i步的近似结果为X_i^t+Δt，则有

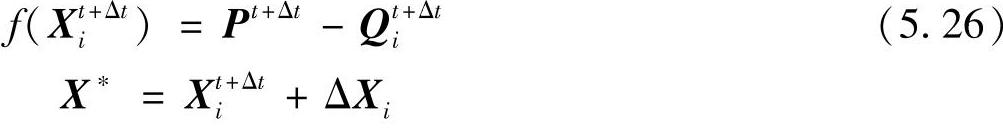
其中，ΔX_i为第i步的近似结果与真值的差。

应用泰勒级数展开，并略去2阶以上高阶项，可得

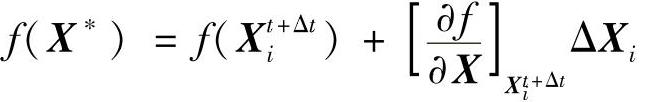
把方程式（5.25）和方程式（5.26）代入上式

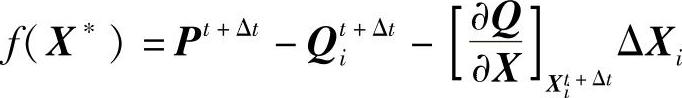
由于f（X^∗）=0，进一步可得

这里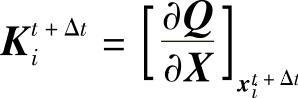，为当前的刚性矩阵（也称为Jacobian矩阵）。于是可以得到以下迭代关系

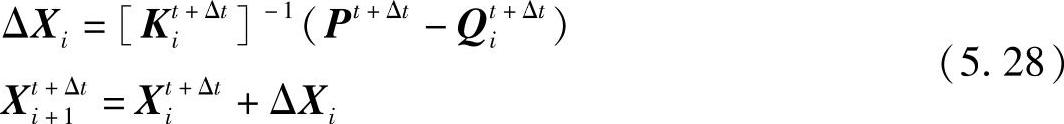
上述迭代的起始点就是时刻t的状态，即X₀^t+Δt=X^t，K₀^t+Δt=K^t。

这就是牛顿迭代法在非线性有限元分析中的运用。

对于复杂的非线性系统，构建每个迭代点的刚性矩阵并进行分解是一个很繁重的工作，有时甚至可能无法精确地得到刚性矩阵，特别是当有限元模型的规模很大时更是如此。所以在实际的非线性有限元分析中，经常结合使用修改牛顿迭代法和拟牛顿迭代法。

对于规模很大但非线性不强的系统，刚性矩阵的变化并不是很大，利用修改牛顿迭代法可能达到提高计算效率的效果。

此外，为了避免直接求解刚性矩阵（微分）的困难，利用弦切法来近似刚性矩阵的拟牛顿迭代法，在某些情况下也会带来较好的效果。拟牛顿迭代法可以表示为(www.xing528.com)

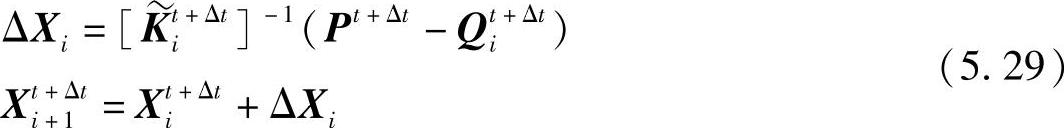
其中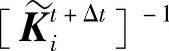，为刚性逆矩阵的近似，且满足以下弦切比例条件

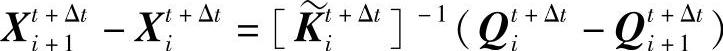
对于刚性矩阵为对称的情况，构建刚性逆矩阵的递推近似的代表方法是BFGS法（Broyden-Fletcher-Goldfarb-Shanno）。这里，对其数学描述不做介绍，有兴趣的读者可以参阅有关参考书。

最后，以非线性结构分析软件Abaqus为例，对非线性问题的求解过程做一下说明。

我们已经说过，在非线性有限元分析中，通常把外力的作用当作一个由零到给定值逐渐变化的假想的时间过程，并在此过程中用迭代方法计算结构的变形或者响应。图5.9所示为结构在外力作用下的非线性变形曲线的示意图。这个曲线上的点的纵坐标反映了变形引起的结构内力。假定在“时刻”t的载荷为P^t，结构的变形为X^t，我们来考虑在一个小的时间增分Δt上把载荷增加到P^t+Δt的情况（ΔP=P^t+Δt-P^t）。由于非线性的原因，显然无法直接求出在P^t+Δt作用下的变形X^t+Δt，而需要在载荷由P^t变化到P^t+Δt的过程上进行若干次迭代运算才能逼近X^t+Δt。

首先，根据ΔP（它代表了指定载荷P^t+Δt与变形X^t引起的节点内力Q^t的差）以及已经得到的时刻t的刚性矩阵K₀^t+Δt，可以决定一个变形增量ΔX^t1+Δt

于是得到一个新的变形响应

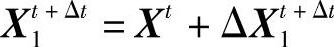
然后可以计算出这个变形所引起的节点内力Q₁^t+Δt。比较给定载荷P^t+Δt与节点内力Q₁^t+Δt，得到力的残差为

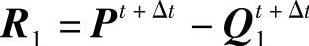
如果力的残差满足‖R₁‖＜ε_F，其中，ε_F为指定的小值，则可以认为外力与内力达到平衡，X₁^t+Δt就是所要求的解；如果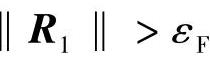，则需要进一步计算。此时，根据更新的刚性矩阵K₁^t+Δt与力的残差R₁，可以确定出下一步迭代的变形增量为

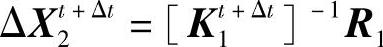
于是得到一个新的变形响应

X₂^t+Δt=X₁^t+Δt+ΔX₂^t+Δt

再次计算力的残差R₂=P^t+Δt-Q₂^t+Δt，并进行收敛性判断。经过若干次这样的迭代运算，最终可以得到收敛于X^t+Δt的解。之后，可以进行下一个时间增分的计算。

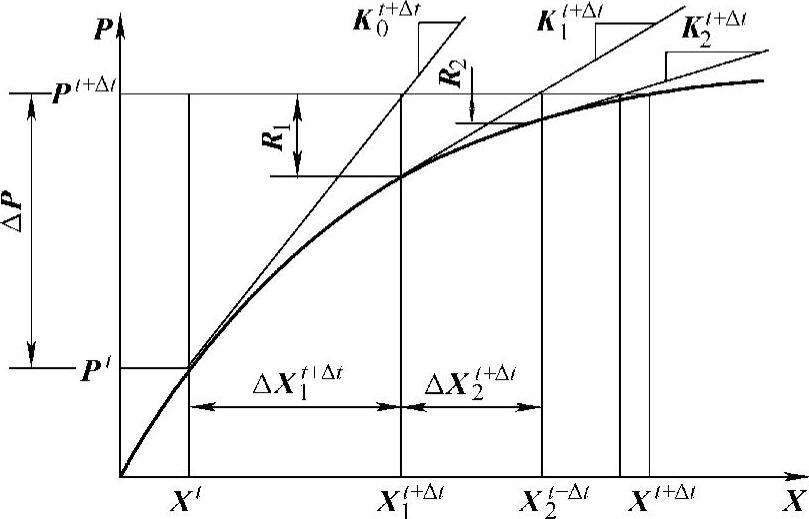
图5.9 结构在外力作用下的非线性变形曲线的示意图

在Abaqus中，收敛性判断的内定值取为ε_F=0.005Q，其中，Q为结构内力的时域平均值。如果迭代进行到i步，力的残差满足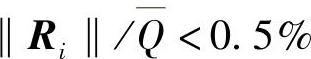，则认为这是一个收敛的解。但是，在进行下一步增分之前，Abaqus还要检查变形增分的大小是否满足以下条件

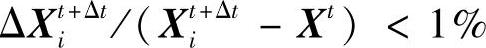
如果同时满足这个条件，才可以进行下一步增分计算，否则，还需要进行新的迭代。

Abaqus的内定准则是：在一个增分Δt上（Increment），最大可以进行16次迭代运算（Iteration）；如果经过16次迭代后仍然不满足收敛条件，则时间增分减小为原来的25%，再进行新的迭代运算。这个过程称为Cutback。内定的最大Cutback回数为5。如果经过5次Cutback后还不能收敛，则终止计算；相反，如果在两个连续的时间增分上仅需少于5次的迭代即可收敛的话，Abaqus自动地把时间增分增加50%，以提高计算效率。经验表明，这个内定准则在大多数情况下可以放心地使用。