拟牛顿迭代法简介及应用

介于牛顿迭代法与修改牛顿迭代法之间，拟牛顿迭代法（Quasi-Newton Method）不直接求解函数f（x）的微分，而是用两点的弦来近似迭代点的微分。所以，这是一种广义的弦切法。

如图5.7所示，可以用迭代点（x₁，y₁）与（x₂，y₂）的连线（弦）来逼近点（x₂，y₂）处的切线（微分）。近似公式为

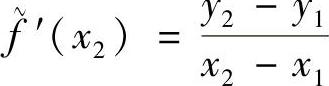
其中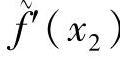，表示f′（x₂）的近似值。下一个迭代点可由下式近似得到

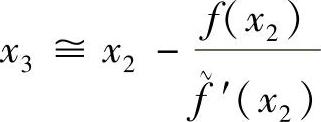
依次类推，可得以下迭代公式

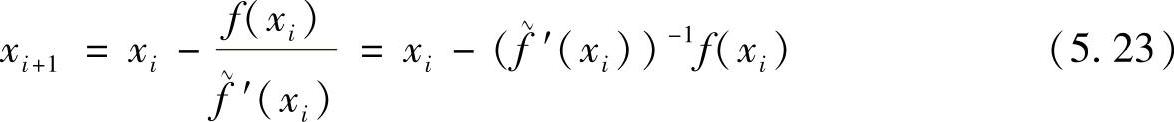
这里，我们用拟牛顿迭代法来求解前面的例题。假定外力与变形无关，考虑第i步迭代的情况，新的迭代步长可由下式近似得到

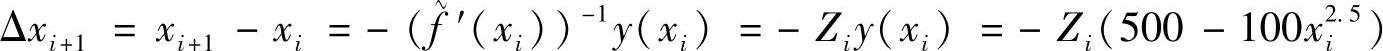
其中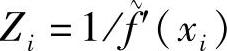，为（x_i，y_i）处的微分的倒数的近似值，即刚性的倒数的近似值（对于多自由度系统，则为刚性矩阵的逆矩阵）。于是可得下一个迭代点的值为(www.xing528.com)

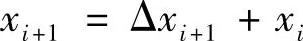
此外，根据公式（5.21）可得

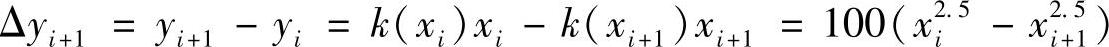
进一步可以得到下一个迭代点的刚性的倒数的近似值为

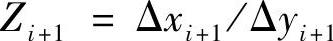
这样，利用以上关系，就可以构建一个不需要严格求解微分的迭代运算关系。

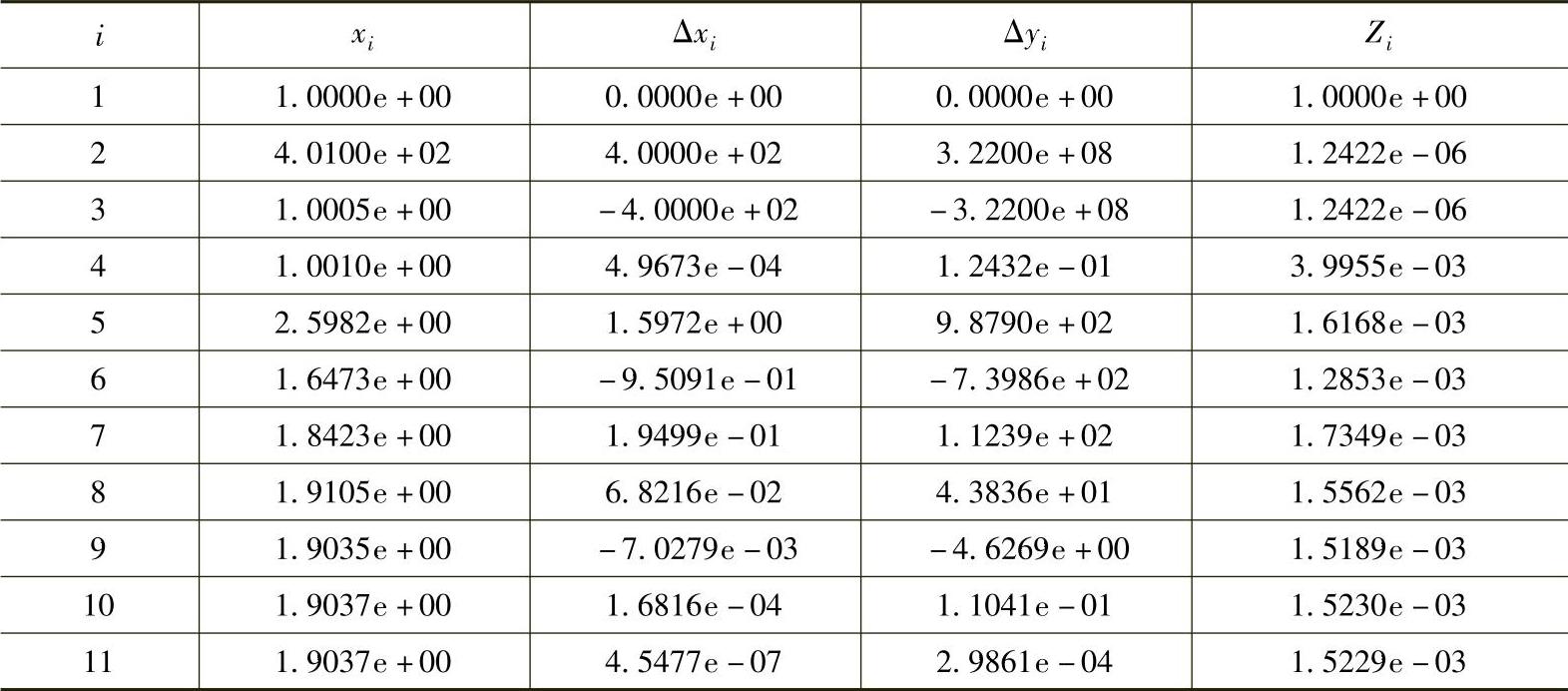
设初始条件为x₁=1.0，Z₁=1.0，迭代运算的结果如表5.3所示。经过10次迭代，即可达到真值（x₁₀=1.9037）。可见，拟牛顿迭代法的收敛速度比牛顿迭代法的要慢，但由于不需要进行微分计算，每次的迭代运算要快，总的计算时间可能会缩短。对于实际的问题，很难预先判断用哪种方法更快更好。一般来说，对于非线性较强的系统，最好采用完全的牛顿迭代法。

表5.3 拟牛顿迭代法的运算结果