牛顿迭代法求解非线性系统响应的优缺点和应用实例

求解非线性系统响应的典型方法是牛顿迭代法，或称Newton-Raphson迭代法。这里，我们以一个单自由度系统为例，对该方法的原理进行介绍。

如图5.5所示，一个圆锥形状的弹簧在外力F的作用下发生变形，弹簧的刚性用k表示，变形用x表示，则有下列关系

F=k（x）x （5.20）

k（x）表示弹簧刚性随着变形x而变化的特性。现在的问题是在给定载荷F的情况下，如何求解变形x。在此，引入一个新的函数f（x）

y=F-k（x）x=f（x） （5.21）

使得y=0的x就是方程式（5.20）的解，即在载荷F作用下的变形，这里我们用x∗来表示。为了探索这个解，可以先假定一个初始值x₁，对应于曲线上（x₁，y₁）的一点。该点的切线方程为

y_T=f（x₁）+f′（x₁）（x-x₁）

其中，导数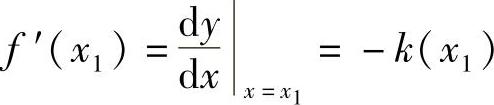为曲线在（x₁，y₁）点的斜率，其值等于在该变形状态下的弹簧刚性。令上式等于0，可以得到该切线与x轴的交点为

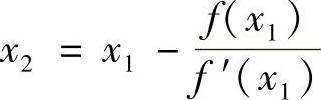
由图5.5可见，x₂比x₁更加接近x^∗。重复同样的步骤，可得进一步逼近真解的x₃为

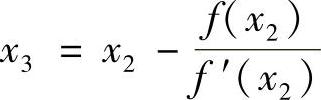
依次类推，可得以下迭代公式(www.xing528.com)

根据这个公式进行迭代运算，即可得到无限逼近真值的解。这便是牛顿迭代法的原理。

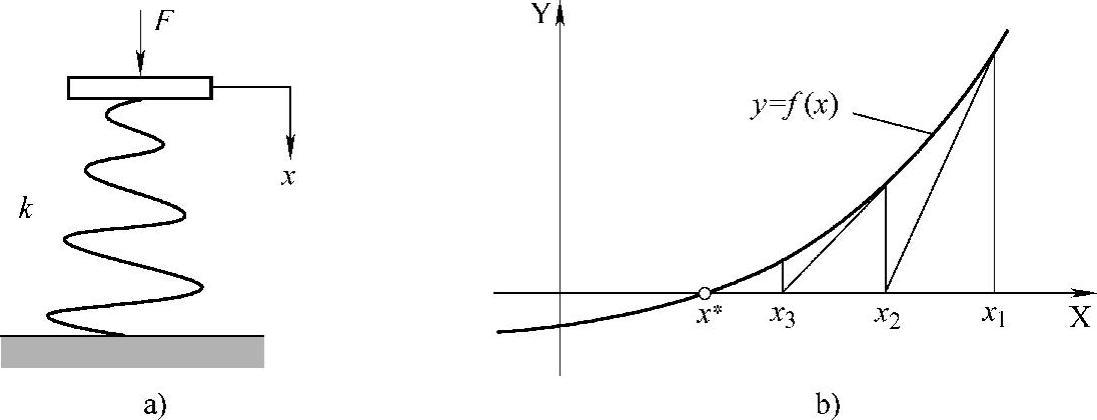
图5.5 对单自由度系统应用牛顿迭代法

a）单自由度系统 b）牛顿迭代法

可以证明，当初始的探索值离开真值不远时，牛顿迭代法具有2阶收敛性，即如果第i步的误差为ε，则第i+1步的误差为ε²。这是牛顿迭代法的重要优点。但是，在以上迭代运算中，每增加一步，都要重新计算一次曲线的导数，也就是说对系统的刚性要进行更新。从计算效率及难度的角度讲，这是牛顿迭代法的主要缺点。此外，对于复杂的非线性系统，如果初始的探索值离开真值较远，则牛顿迭代法可能探索不到真值。

作为应用举例，假定图5.5中的弹簧刚性与变形的关系为k（x）=100x^1.5，用牛顿迭代法求解在F=500N作用下的弹簧变形。

由关系式（5.20）可得500=100x^2.5，即5=x^2.5。为了求解这个非线性方程，构建一个新的函数f（x）=5-x^2.5，且有f′（x）=-2.5x^1.5。假定一个初估值x₀=1，应用牛顿迭代法，可得

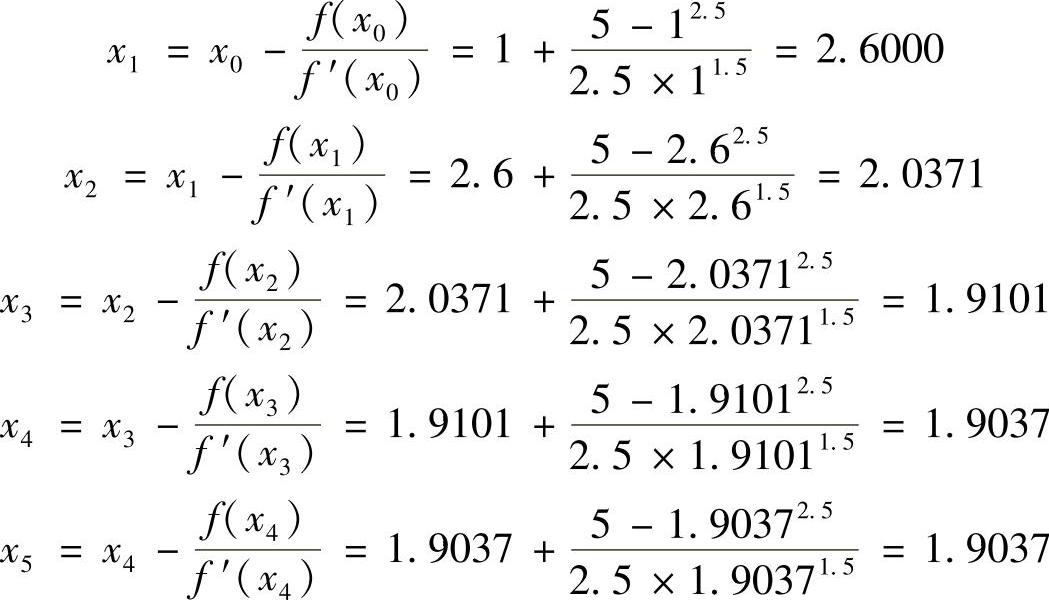
可见，经过4步迭代运算，方程的解收敛于x=1.9037。