解决非线性代数方程组的方法

上节中讨论了线性代数方程组[A]{x}={b}的解法。所谓线性，是指系数矩阵[A]保持不变，输出响应{x}与输入{b}之间呈现比例变化的关系。这种系统满足线性叠加的原理，即系统在众多载荷作用下的响应等于单个载荷作用下的响应之和。显然，如果系数矩阵[A]随着输入{b}而变化，则输出响应{x}与输入{b}之间呈现非线性的关系，这时将无法直接求解该方程。本节将讨论这种非线性方程的解法。

实际中，完全理想的线性系统是不存在的，任何系统都具有或强或弱的非线性。尽管在很多情况下，把研究对象当作线性系统来对待足以满足设计要求，但在某些情况下，则需要考虑非线性要素的影响。

在结构力学中，引起非线性的要素主要有以下三个方面（见图5.4）：

①材料非线性。材料非线性是指应力（负载）与应变（变形）呈现非线性的变化关系。如橡胶等超弹性材料，在弹性范围内，其应力与应变之间也呈现很强的非线性。对于金属材料，当负载过大超过其弹性范围时，则表现出极强的非线性。

②几何非线性。在结构力学中，如果结构的变形或位移响应相对于其尺度非常小，往往可以用线性系统理论来描述；但如果变形较大时，则应考虑由此带来的几何非线性。(www.xing528.com)

③边界条件非线性。如果在负载作用下，系统的边界条件发生变化，如两个部件由初期的非接触变为接触，则应考虑由此产生的非线性。对于初期处于接触状态的系统来说，由于摩擦的作用，该系统也属于非线性系统。

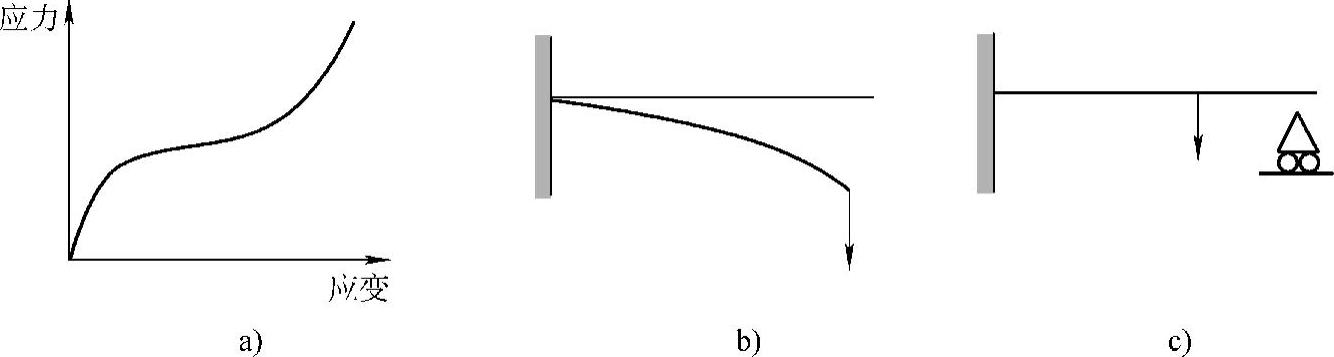
图5.4 非线性的类型

a）材料非线性 b）几何非线性 c）边界条件非线性