线性代数方程的迭代求解方法

以上介绍的以高斯消去法为基础的直接解法是最常用的方法。对于一个n×n矩阵，高斯消去法的运算量大约为2n³/3。对于节点数很大的有限元模型（现在，上百万节点的汽车车身模型已很平常），高斯消去法的计算量将很可观，有些情况下，即使用最强大的计算机也可能满足不了对计算时间的要求。在这种情况下，迭代算法为解大规模线性代数方程组提供了另一种选择（在计算流体力学领域，主要是运用迭代法求解）。

1.迭代解法的概念

首先，以下列三元一次方程组为例，来对迭代解法的概念加以说明。

该方程组的真解为x₁=-1，x₂=1，x₃=1。把方程组（5.6）变形为

迭代解法就是根据方程组（5.7）构建下列递推运算关系（i=0，1，2，3，…）

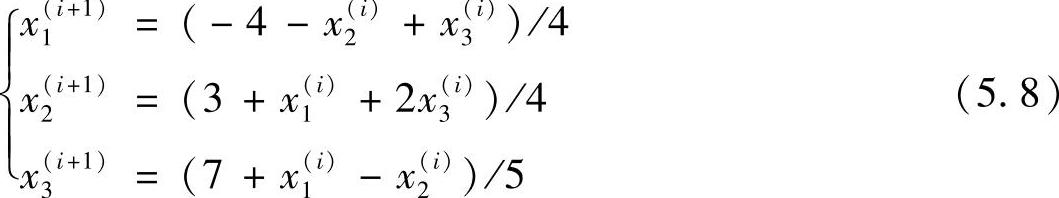
例如取初始估计值为x₁^（0）=0、x₂^（0）=0、x₃^（0）=0，则经过10次迭代即可逼近真实解（见表5.1）。

在以上所示的方法中，方程组（5.8）等号右边并没有及时地引入最新的计算结果。例如第1个方程已经计算出了x₁^（i+1），而在第2、3个方程中仍然使用前面一步的值x₁^（i）。如果把最新的计算结果也引入到迭代运算中，则可以得到下列关系

取同样的初始估计值x₁^（0）=0、x₂^（0）=0、x₃^（0）=0，只需5次迭代，即可逼近真实解（见表5.2），即计算速度提高了1倍。可见，方程组（5.9）是对方程组（5.8）的一个改进。

表5.1 根据方程组（5.8）所进行的迭代运算

表5.2 根据方程组（5.9）所进行的迭代运算

对于这个简单的例子，应用迭代算法并不见得比直接解法（高斯消去法、FBS法）求解速度快。当系统规模越来越大时，迭代算法的优点就会显露出来。特别是当系数矩阵中含有大量0元素（稀疏矩阵）时，迭代算法的占用内存少，计算速度快的优点会很突出。

2.Jacobi法和Gauss-Seidel法

上面所介绍的迭代运算过程实际上代表了两种重要的古典迭代方法。方程组（5.8）所代表的方法称为Jacobi法，方程组（5.9）所代表的方法称为Gauss-Seidel法。

把方程组的系数矩阵[A]分为对角项[D]、对角线以下的项[L]以及对角线以上的项[U]之和（注意：这不同于前节介绍的LU分解）

[A]=[D]+[L]+[U]

具体到上面的例子，有

则Jacobi法可以表示为

Gauss-Seidel法可以表示为

应该指出的是，对于所有的线性代数方程，上述迭代算法并不能保证都收敛。例如对于式（5.1a）、式（5.1b）和式（5.1c）所示的方程，不管是用Jacobi迭代法还是用Gauss-Seidel迭代法，都将发散。迭代算法收敛的充分条件是系数矩阵[A]的对角项的绝对值大于所在行上其余项的绝对值之和，即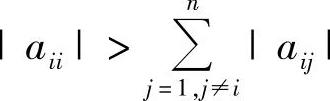。但是，这个充分条件并不是十分严密，可能会有Jacobi法收敛而Gauss-Seidel法不收敛的情况。有时，即使不满足这个条件，但对角项的绝对值为最大，也可能收敛。对于收敛条件的详细表述，这里就不做介绍。

3.最速下降法（Steepest Descent Method）

适用范围更宽的迭代算法是基于最小值探索的方法，即由线性方程构建一个2次型函数，通过探索其最小值而求得方程的解。

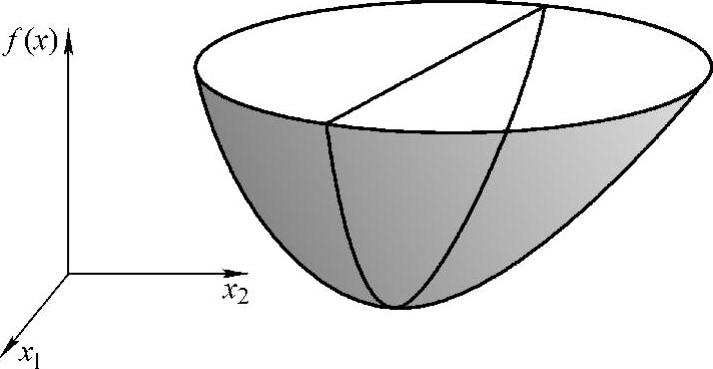
图5.12 次型函数f（x）的形状的示意图

对于方程[A]{x}={b}，定义下列2次型函数

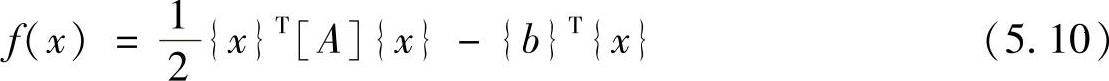
f（x）的结果为一个数，而不是向量。定义上述2次型函数的梯度为

这是一个向量，其方向取为f（x）的最大增加方向。将式（5.10）代入式（5.11）进行整理，可得

当[A]为对称矩阵时，上式成为

{f′（x）}=[A]{x}-{b}

如果令梯度为0，则得[A]{x}={b}。可见，2次型函数f（x）的极点（梯度为0的点）就是线性方程组的解。因此，求解方程[A]{x}={b}的问题就演变成了探索2次型函数f（x）的极点的问题。对于线性动力学系统，矩阵[A]为正定矩阵，可以证明与其对应的2次型函数f（x）的形状为“碗形”，其极点处于碗底（参见图5.1），因此，从给定初始位置出发，下降到碗底的过程就是方程求解的过程。

最直接了当的方法就是从最陡的方向下降，这就是所谓的最速下降法（Steepest Descent Method），或称梯度下降法（Gradient Descent Method）。最陡的方向即是{f′（x）}的反方向，-{f′（x）}={b}-[A]{x}。

假设我们从{x^（0）}出发，经过若干步{x^（1）}，{x^（2）}，…，{x^（i）}下降到碗底，逼近方程的解{x}。定义误差为{g^（i）}={x^（i）}-{x}，残差为{r^（i）}={b}-{x^（i）}。可见，残差的方向就是最陡下降方向，即{r^（i）}=-{f′（x）}。因而，我们可以在此方向上定义以下递推关系

现在的问题是如何确定式（5.12）中的系数α^（i）。我们的目标是探索2次型函数f（x）的最小值，因此，α^（i）应该使得在式（5.12）所示的探索方向上f（x）为最小。这种在一个方向上探索f（x）极值的方法称为线搜索（Line Search）。应用微分法则

上式为0时，f（x）为最小。可见，应该选择α^（i）使得{r^（i+1）}与{r^（i）}正交，即(www.xing528.com)

{r^（i+1）}T{r^（i）}=0

由于

代入上式后整理，可得

将以上结果整理，用最速下降法进行迭代运算的过程可以表示为

该方法的特点就是每次探索的方向总是沿着残差的方向，而且当前的探索方向总与上一个探索方向直交（但应注意：并没有说当前的探索方向与以前的所有探索方向正交）。事实上，最速下降法往往会“重蹈覆辙”，在同一个方向上探索多次。这些特点可以从图5.2的实例中看出。该图是对一个二元一次方程组应用最速下降法的例子。

从初始值（x₁=-2，x₂=-2）开始，经过6步探索过程，逼近真值（x₁=2，x₂=-2）。

4.共轭梯度法（Conjugate Gradient Method）

在商业有限元软件中，共轭梯度法是常被采用的迭代方法。这里的共轭并不是复数共轭的概念，而是指两个长度为n的非零向量{u}、{v}具有以下关系

{u}^T[A]{v}=0也称{u}、{v}相对于（n×n）的矩阵[A]正交。可以证明，如果可以找到n个互为共轭的向量{d（i）}（i=0，1，…，n-1），则方程[A]{x}={b}的解可以表示为这n个互为共轭的向量的线性组合：

写成迭代运算的形式，就是

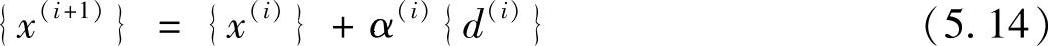
可见，在不考虑数值舍入误差的理想情况下，只需要进行n次迭代运算，即可得到方程的解。这就是共轭梯度法的基本原理。

例如对一个二元一次方程组，只需两步迭代即可得到结果；而最速下降法则需要两次以上的迭代运算（在同一个方向上可能进行多次，参见图5.2）。也就是说，共轭梯度法的收敛性要比最速下降法的好，这正是该方法为商业有限元软件所青睐的原因。事实上，对于大规模系统，并不需要找到所有n个互为共轭的向量，也可以逼近方程的解。

图5.2 最速下降法的例子

现在来探讨共轭探索方向{d（i）}的特点。与最速下降法一样，α（i）应该使得在式（5.14）所示的探索线路上的2次型函数f（x）为最小。应用微分法则

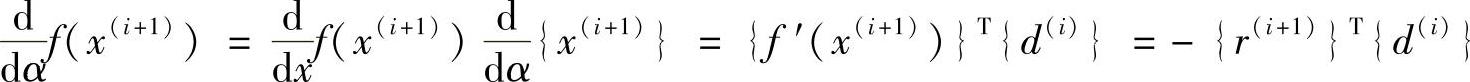
上式为0时，f（x）为最小。可见，应该选择α（i）使得{r（i+1）}与{d（i）}正交，即

由于，式（5.15）可进一步写成

即第（i+1）步的误差方向与第i步的探索方向为共轭关系。另外，由式（5.14）可得误差的递推关系为

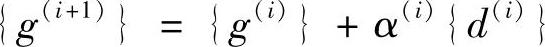
代入式（5.16）整理可得（利用关系{r（i）}=-[A]{g（i）}）

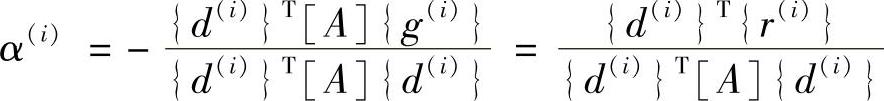
现在的问题是如何构建互为共轭的向量{d^（i）}（i=0，1，…，n-1）。很自然，初始探索方向可取为残差方向，{d^（0）}={r^（0）}={b}-[A]{x^（0）}。这点与最速下降法相同。但从第2步开始（i＞0），共轭梯度法的探索方向{d^（i+1）}对最速下降法的探索方向{r^（i+1）}做以下修改

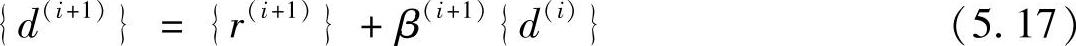
即从第2步开始（i＞0），共轭梯度法的探索方向{d^（i+1）}偏离了残差方向。这是与最速下降法不同的地方。通过选择式（5.17）中的系数β^（i+1），来保证{d^（i）}满足互为共轭的条件。

给方程式（5.17）两边同乘{d^（i）}^T[A]，得

为了满足共轭条件{d^（i）}^T[A]{d^（i+1）}=0，β^（i+1）应该取为

方程式（5.18）含有第（i+1）步的残差{r^（i+1）}，可以通过下式算出：

从方程式（5.17）及（5.18）看，好像只能说明{d^（i+1）}与{d^（i）}互为共轭，但事实上，{d^（i+1）}也满足与{d^（0）}，{d^（1）}，…，{d^（i-1）}互为共轭的条件。这是共轭梯度法最大的优点。详细的证明在这里就不做说明。

归纳起来，用共轭梯度法进行迭代运算的过程可以表示为

对前面所示例子应用共轭梯度法进行迭代运算（见图5.3），从初始值（x₁=-2，x₂=-2）开始，经过两步探索过程，即可到达真值（x₁=2，x₂=-2）。

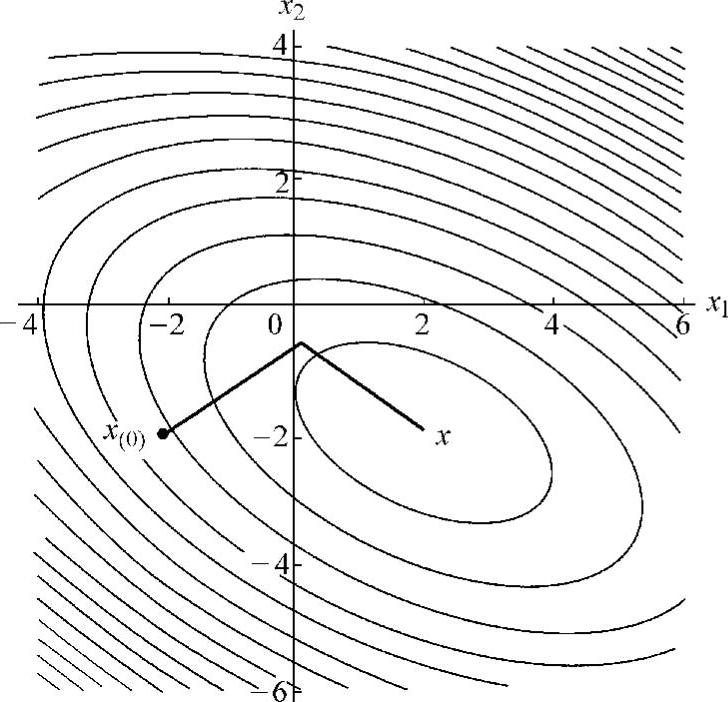
图5.3 共轭梯度法的例子