结合刚性影响的模态模型构建方法

上节介绍了利用传递函数综合法把实验结果与有限元模型相结合的混合分析方法。一个子结构的动特性不光用传递函数可以表现，也可以用模态参数（固有频率、模态形状、模态阻尼）来表示。这样得到的模型称为模态模型（Modal Model）。模态模型可以由模态实验得到（通过对传递函数进行曲线拟合来确定模态参数），也可以由数学模型的特征值分析得到。

模态模型由模态自由度和对应的模态参数组成。假定对图4.11中的子结构进行模态分析，得到n个模态，则有n个模态自由度，用q_i（i=1，2，…，n）来表示。每个模态可以看作为由模态质量、模态刚性以及模态阻尼构成的单自由度系统。对于常用的质量正规化的情况，模态质量为1，模态刚性等于固有角频率的平方。已知模态参数后，子结构上的任意点的响应可以由模态叠加法得到。例如对于结合点a、b来说，其X、Y方向上的响应可以表示为

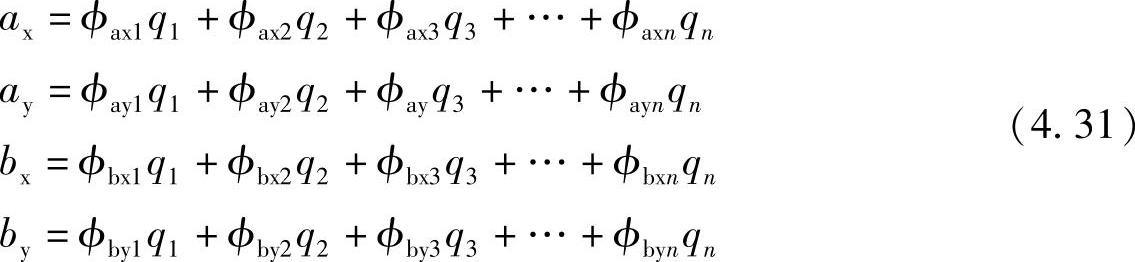
其中，ϕ_ax1表示第一个模态在a点X方向上的模态形状，其余定义类推。当然，子结构上其他点的响应也可以用同样方法得到。

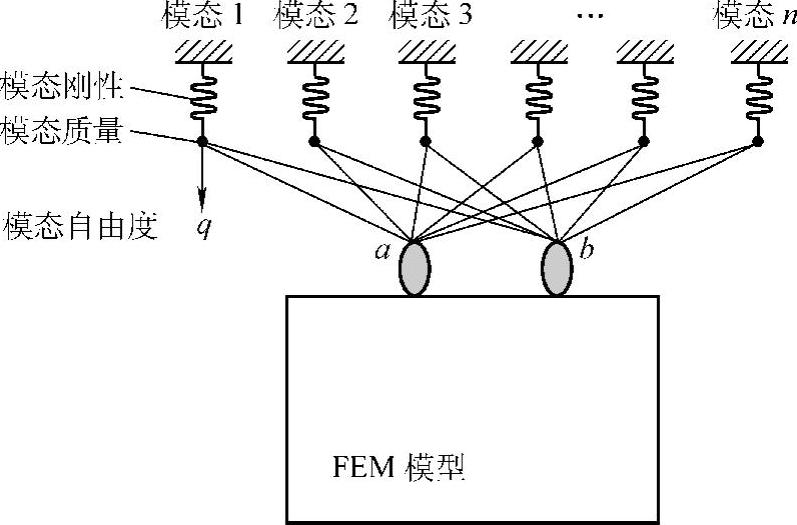
式（4.31）所示的关系在有限元软件中可以用多点约束方程（Multiple Point Con-straint，MPC）来表示，而模态质量、模态刚性、模态阻尼可以用集中质量元素、集中刚性元素和集中阻尼元素来表示。这样，子结构的模态模型可以方便地导入到主体结构的有限元分析模型中来，如图4.15所示。为了简洁，在图4.15中略掉了阻尼元素。

在实验模态分析中，0Hz的刚体模态可能无法得到，在构建模态模型时，应加入子结构的刚体特性。这可以在重心位置用集中质量元素定义其质量和惯性，然后把重心节点与需要的点（结合点以及需要响应输出的点）用刚性元素相连即可。如果不考虑刚体特性，可能会引起较大的低频误差；如果从有限元模型通过特征值分析来构建模态模型，0Hz的刚体模态可以直接考虑进来，把刚体模态与弹性模态同时考虑即可。当然，如果子结构从主体结构分离后仍存在其他约束，则应在此约束条件下进行模态分析。这时，不存在刚体模态问题。

(www.xing528.com)

图4.15 子结构模态模型与主体结构有限元模型的结合

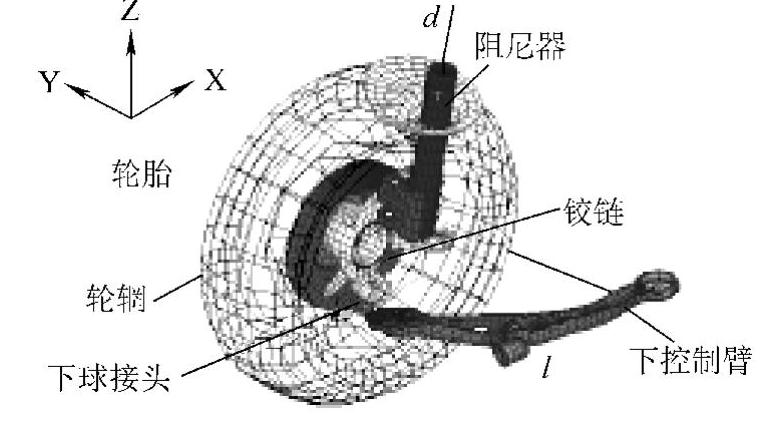
图4.16 轮胎模态模型与悬架有限元模型相结合

上述模态模型的构建方法显然没有考虑与主体结构结合部的刚性的影响。当子结构本身的刚性远高于结合部刚性（柔性结合的情况）时，这种方法精度较高；但如果结合部刚性很高，以至于对子结构动特性的影响较大时，用这种方法进行综合，可能会产生较大误差。前面介绍的子结构模态综合法和传递函数综合法在原理上是严密的，但是实际中存在误差。子结构模态综合法的误差源于固定边界模态的截止误差，传递函数综合法的误差源于测量误差以及矩阵求逆运算的数值误差，而这里介绍的模态模型化方法的误差源于其原理上的不严密性，这是该方法本质上的缺陷。但是，由于该方法简单明了、易于运用，在实际中得到很多应用。例如在研究汽车的低频振动问题时，研究对象是底盘系统。过去一般把车体当作刚体来看待，但现在往往需要考虑到车体动特性的影响。如果用普通的有限元模型来表示车体的话，会增加很大的计算负担，因此，通常把车体转化为模态模型。轮胎的模型化也是这样，经常把由实验模态分析得来的模态模型导入到整车的有限元分析模型中去。图4.16所示为一个把轮胎模态模型与悬架有限元模型相结合的例子。

为了改进精度，在建立模态模型时，应尽量纳入更多的模态。最有效的方法是把子结构进行Craig-Bampton缩减后再进行固有值分析，进而转化为模态模型。这样，操作上可能比用子结构模态综合法直观易懂，精度又可以保证。但是，这种方法对于实验模态分析来说无法运用。